

回路电流法
电子常识
描述
回路电流法
回路电流法是以一组独立回路电流作为变量列写电路方程求解电路变量的方法。倘若选择基本回路作为独立回路,则回路电流即是各连支电流。
如图2-3-1所示,已知 ,要求
,要求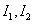 和
和 。这里仍然沿用介绍支路电流法的例题,现将运用回路电流法求解。首先选择
。这里仍然沿用介绍支路电流法的例题,现将运用回路电流法求解。首先选择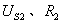 所在支路为树支(用粗线条表示),如图选择各支路参考方程,以连支电流
所在支路为树支(用粗线条表示),如图选择各支路参考方程,以连支电流 作为变量,那么树支电流就可以用连支电流表示,即:
作为变量,那么树支电流就可以用连支电流表示,即: (式2-3-1),然后对两个独立回路列写KVL方程,即:
(式2-3-1),然后对两个独立回路列写KVL方程,即:
 (式2-3-2),
(式2-3-2),
 (式2-3-3)
(式2-3-3)

图2-3-1
将(式2-3-1)代入(式2-3-2)与式(2-3-3),整理得到:

 ;
;  ;
;  。
。
如果将图2-3-1中 的参考方向反一下变为
的参考方向反一下变为 ,基本回路
,基本回路 的取向也反一下为
的取向也反一下为 ,那么有:
,那么有:



归纳(式2-3-4)—(式2-3-7),可以得到运用回路电流法列写基本回路电流方程的一般式:

在(式2-3-8)(式2-3-9)中,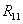 称为
称为 回路的自电阻,等于
回路的自电阻,等于 回路中各电阻之和,恒为正;
回路中各电阻之和,恒为正; 称为
称为 回路的自电阻,等于
回路的自电阻,等于 回路中各电阻之和,恒为正;
回路中各电阻之和,恒为正; 称为
称为 回路的互电阻,等于
回路的互电阻,等于 两个回路的公共支路电阻。当
两个回路的公共支路电阻。当 流经公共电阻时方向一致,互电阻为正,反之,互电阻为负。(式2-3-8)(式2-3-9)中方程的右边是各个独立回路中各电压源电压的代数和。当各电压源电势与回路方向一致时,相应电压源电压取正;反之,取负。
流经公共电阻时方向一致,互电阻为正,反之,互电阻为负。(式2-3-8)(式2-3-9)中方程的右边是各个独立回路中各电压源电压的代数和。当各电压源电势与回路方向一致时,相应电压源电压取正;反之,取负。
当电路中含有电流源、受控源时,其处理方法与支路电流法相同,请看例题。

图2-3-2 例2-3-1附图
例2-3-1 如图2-3-2 所示电路中,已知:, ,,
,, ,,试用回路电流法求各支路电流。
,,试用回路电流法求各支路电流。
解:图2-3-2中含有两个电流源,电流源所在支路应尽可能放在连支上,因而选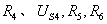 所在支路为树(用粗线条表示),如图选择各支路电流参考方向,画出3个基本回路,根据回路电流法,列出:
所在支路为树(用粗线条表示),如图选择各支路电流参考方向,画出3个基本回路,根据回路电流法,列出:
 ,
, ,
, 
代入已知数据得到:
例2-3-2 如图2-3-3所示,已知: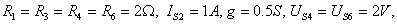 求各支路电流。
求各支路电流。

图2-3-3 例2-3-2附图
解:如图选择各支路电流参考方向,选择 所在支路为树支(用粗线条表示),画出三个基本回路,有:
所在支路为树支(用粗线条表示),画出三个基本回路,有:

附加方程: ,代入已知数据求解得到:
,代入已知数据求解得到:

- 相关推荐
- 热点推荐
- 电流法
-
回路电流法的步骤及应用2024-08-09 5751
-
回路电流法分析电路是什么的体现2024-08-07 2227
-
网孔电流法和回路电流法的区别和联系2024-03-01 8437
-
回路电流法 (1)#电路未来加油dz 2023-09-03
-
如何去处理在回路电流法中的无伴电流源呢2021-10-09 2889
-
网孔电流法和回路电流法有何关系2021-09-30 5360
-
支路电流法和回路电流法区别2021-01-15 20103
-
回路电流法怎么理解_回路电流法解析2017-12-21 52065
全部0条评论

快来发表一下你的评论吧 !

