

一阶电路的零输入响应
电子常识
描述
仅含一个独立储能元件的电路称为一阶电路。当电路中没有激励,仅由储能元件的初始储能引起的响应,称为零输入响应。
一、RC电路的零输入响应
如图8-4-1所示电路,开关S原在位置1,电路已达稳态,电压源电压为 ,则
,则 。在
。在 时刻,S由1切换至2,下面推求零输入响应
时刻,S由1切换至2,下面推求零输入响应 、
、 。
。

图8-4-1
当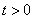 ,S切换至2后,由
,S切换至2后,由 得:
得:
 (式8-4-1)
(式8-4-1)
将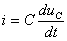 代入上式得:
代入上式得:
 (式8-4-2)
(式8-4-2)
(式8-4-2)是一个一阶线性常系数齐次微分方程,其特征方程为:
特征根为:

齐次方程的通解为:
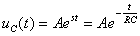 (式8-4-3)
(式8-4-3)
(式8-4-3)中的积分常数A由初始条件确定。由换路定则得: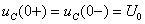 ,代入(式8-4-3),则有:
,代入(式8-4-3),则有:

于是:
 (式8-4-4),
(式8-4-4),  (式8-4-5)
(式8-4-5)
(式8-4-5)中的负号表示实际的电容放电电流方向与假设的参考方向相反。 还可以这样求,即:
还可以这样求,即:

图8-4-2绘出了 、
、 的曲线图,它们都按指数规律衰减。
的曲线图,它们都按指数规律衰减。

图8-4-2
在(式8-4-4)和(式8-4-5)中,含 ,
,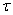 具有时间的量纲,因而称为电路的时间常数。当C为1法拉
具有时间的量纲,因而称为电路的时间常数。当C为1法拉 ,R为1欧姆
,R为1欧姆 时,
时, 为1秒。时间常数
为1秒。时间常数 的大小反映了过渡过程进展的快慢。
的大小反映了过渡过程进展的快慢。 越大,过渡过程维持的时间越长、过渡过程进行得越慢;
越大,过渡过程维持的时间越长、过渡过程进行得越慢; 越小,过渡过程维持的时间越短、过渡过程进行得越快。
越小,过渡过程维持的时间越短、过渡过程进行得越快。
下面以电容电压的衰减曲线为例,介绍求时间常数 的图解法。在图8-4-3中,从衰减曲线上任一点P作切线,它与t轴的交点为,从P点作t轴的垂直线,与t轴的交点为P’,则:
的图解法。在图8-4-3中,从衰减曲线上任一点P作切线,它与t轴的交点为,从P点作t轴的垂直线,与t轴的交点为P’,则:
通过实验得出或i的衰减曲线,再由图解法求出,这在实际工作中是一种有用的方法。
图8-4-3
时间常数 的大小取决于电路的结构和参数,而与激励无关。
的大小取决于电路的结构和参数,而与激励无关。 串联电路的时间常数
串联电路的时间常数 。R、C愈大,
。R、C愈大, 愈大。当R一定、C愈大,则电容C上储存的初始能量
愈大。当R一定、C愈大,则电容C上储存的初始能量 越大,放电时间愈长;当C一定、R愈大,则放电电流愈小,放电时间愈长。
越大,放电时间愈长;当C一定、R愈大,则放电电流愈小,放电时间愈长。
二、电路的零输入响应
如图8-4-4所示电路,电压源电压为,开关S原置于位置1,且电路已达稳态,此时电感相当于短接,。当 时,开关S由1切换至2,求零输入响应
时,开关S由1切换至2,求零输入响应 、。
、。

图8-4-4
开关切换至2后,如图8-4-4选定参考方向,由 得到:
得到:
(式8-4-7)
(式8-4-7)是一个一阶线性常系数齐次微分方程,其特征方程为:

特征根为:
 (式8-4-8)
(式8-4-8)
齐次方程的通解为:
 (式8-4-9)
(式8-4-9)
(式8-4-9)中的积分常数A由初始条件确定。
由换路定则:
 (式8-4-10)
(式8-4-10)
由(式8-4-9):

于是:
,  (式8-4-11)
(式8-4-11)
可见换路后,电流 从初值按指数规律衰减,最终衰减至零,如图8-4-5所示。
从初值按指数规律衰减,最终衰减至零,如图8-4-5所示。

图8-4-5
电阻电压:
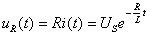 (式8-4-12)
(式8-4-12)
电感电压:
(式8-4-13)
、相差一个负号,两者的变化规律都与电流相同。它们随时间变化曲线亦示于图8-4-5中。
在(式8-4-11)至(式8-4-13)中,含 ,
, 具有时间的量纲,当R为1欧姆
具有时间的量纲,当R为1欧姆 ,L为1亨利,则
,L为1亨利,则 为1秒,与
为1秒,与 电路中的时间常数一样,它反映了过渡过程进展的快慢。
电路中的时间常数一样,它反映了过渡过程进展的快慢。
- 相关推荐
- 热点推荐
- 一阶
-
什么样的电信号可以作为RC一阶电路零输入响应的激励信号呢?2023-11-21 6649
-
电路知识:一阶电路的零输入响应(上)(1)(3)#电路知识学习硬声知识 2023-01-11
-
电路知识:一阶电路的零输入响应(002)(2)#电路知识学习电子 2023-01-10
-
[2.3.1]--一阶电路的零输入响应学习电子知识 2022-11-25
-
[7.3.1]--3.9.1-一阶电路零输入响应李开鸿 2022-11-12
-
6-2 一阶电路的零输入响应2012-05-10 306
-
一阶电路的响应测试2008-11-02 11806
-
RC一阶电路的响应测试2008-09-24 75954
全部0条评论

快来发表一下你的评论吧 !

