拉普拉斯变换

拉普拉斯变换

 在电路分析中，如果将换路时刻作为时间的起点，那么我们只需研究后的电路变量，这样就可以将函数限定在的区间。这就相当于将函数乘上了单位阶跃函数，即：

乘以一个衰减因子，选择适当的，使得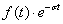在区间内绝对可积，则它的傅里叶变换为：

     （式9-1-1）

（式9-1-1）的积分下限取为，令，则积分结果是S的函数，将（式9-1-1）写为：

     （式9-1-2）

（式9-1-2）中的s称为复频率。对于一个时间函数，由（式9-1-2）就可得到一个，通常将称为原函数，将称为象函数。

对进行傅里叶反变换，有：

上式两边同乘，得：

     （式9-1-3）

（式9-1-2）、（式9-1-3）是一对拉普拉斯变换式，（式9-1-2）为拉普拉斯正变换，（式9-1-3）为拉普拉斯反变换，常用手写体“L”表示拉普拉斯变换，记为：

，

如果时间函数满足：

（1）时，；

（2）时，和都分段连续，在有限区间内至多存在有限个间断点；

（3）是指数阶函数，即存在常数和，使，从而使积分有限，其中、，则的拉普拉斯变换存在。电路中常见函数一般都是指数阶函数。

 

下面按拉普拉斯变换的定义式（式9-1-2）导出一些常用函数的象函数。

一、指数函数

这里应有。

当时，成为单位阶跃函数，于是的拉氏变换为，记为：

当时，可得：

二、单位冲激函数

式中利用了的筛分性质，即：

一些常用函数的拉普拉斯变换式详见表9-1-1。

 

表9-1-1  一些常用函数的拉普拉斯变换

	1
（n为正整数）
（n为正整数）