

拉普拉斯变换的基本定理
电子常识
2681人已加入
描述
拉普拉斯变换的基本定理
打开APP阅读更多精彩内容
本节介绍拉普拉斯变换(也称为拉氏变换)的基本性质,了解掌握了这些性质,可以更加方便地求解各种拉普拉斯正反变换。
一、线性定理
设  则:
则:
 (式9-2-1)
(式9-2-1)
式中 为常系数。
为常系数。
例9-2-1 求 、
、 和
和 的拉氏变换。
的拉氏变换。
解:

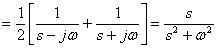
同理:


二、微分定理
设  ,则:
,则:
 (式9-2-1)
(式9-2-1)
同理可推广得到 的高阶导数的拉氏变换式:
的高阶导数的拉氏变换式:

例9-2-2:
已知 ,求
,求 。
。
解:由于 ,由(式9-2-2)得:
,由(式9-2-2)得:

同理:

三、积分定理
设 ,则:
,则:
 (式9-2-3)
(式9-2-3)
例9-2-3 求 。
。
解:斜坡函数 是单位阶跃函数
是单位阶跃函数 的积分,由(式9-2-3)得:
的积分,由(式9-2-3)得:

四、时域位移(延时)定理
设 ,则:
,则:
 (式9-2-4)
(式9-2-4)
例9-2-4:求图9-2-1所示函数 的拉普拉斯变换式。
的拉普拉斯变换式。

解:由图可知:


五、复频域位移定理
设 ,则:
,则:
 (式9-2-5)
(式9-2-5)
例9-2-5:已知
求: 和
和 的拉普拉斯反变换。
的拉普拉斯反变换。
解:利用复频域位移定理:

六、卷积定理:
设 ,则:
,则:
 (式9-2-6)
(式9-2-6)
例9-2-6.求 的拉普拉斯反变换式。
的拉普拉斯反变换式。
解:已知,利用卷积定理得:
同理可推得:
七、初值定理
设 ,则
,则
例9-2-7.设 ,验证初值定理。
,验证初值定理。
解:


又:
 ,所以,得证!
,所以,得证!
八、终值定理:
设 ,则
,则
例9-2-8.仍设 ,验证终值定理。
,验证终值定理。
解:

 ,又
,又
所以,得证!
注意:利用终值定理求的前提条件是必须存在,且是唯一确定的值。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
- 相关推荐
- 热点推荐
- 拉普拉斯
-
拉普拉斯变换的意义2023-09-07 6588
-
拉普拉斯变换表下载2021-12-30 1014
-
拉普拉斯变换在现代控制领域有哪些应用?2021-04-29 2675
-
计算机Fortran编程实现偏微分方程拉普拉斯变换2020-08-14 3424
-
拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表2017-12-05 266092
-
拉普拉斯变换及其应用_elecfans.com2015-10-28 1298
-
拉普拉斯变换的基本性质.ppt2009-09-16 3233
-
拉普拉斯变换视频教程2009-09-03 6972
-
拉普拉斯变换2009-07-27 6134
-
拉普拉斯变换课件教案2009-07-09 684
-
什么是拉普拉斯变换2009-07-08 7484
全部0条评论

快来发表一下你的评论吧 !

