

拉普拉斯反变换
电子常识
2655人已加入
描述
拉普拉斯反变换
打开APP阅读更多精彩内容
利用拉普拉斯反变换的定义式(9-1-3),将象函数 代入式中进行积分,即可求出相应的原函数
代入式中进行积分,即可求出相应的原函数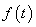 ,但往往求积分的运算并不简单。下面介绍求反变换的一种校为简便的方法。
,但往往求积分的运算并不简单。下面介绍求反变换的一种校为简便的方法。
设有理分式函数:

若m≥n,则 可通过多项式除法得:
可通过多项式除法得:

式中,整式 的拉普拉斯反变换为:
的拉普拉斯反变换为:

 是有理真分式,记为。对于电路问题,多数F(S)是有理真分式即n≥m情况。为求
是有理真分式,记为。对于电路问题,多数F(S)是有理真分式即n≥m情况。为求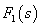 的拉普拉斯反变换,通常利用部分分式展开的方法,将之展开成简单分式之和。简单分式的反变换,可直接查表9-1-1直接获得。
的拉普拉斯反变换,通常利用部分分式展开的方法,将之展开成简单分式之和。简单分式的反变换,可直接查表9-1-1直接获得。
令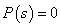 ,求出相应的几个根,记作
,求出相应的几个根,记作 。根据所求根的不同类型,下面分三种情况进行讨论。
。根据所求根的不同类型,下面分三种情况进行讨论。
一、当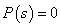 有几个不相同的实数根时
有几个不相同的实数根时
 按部分分式展开为:
按部分分式展开为:
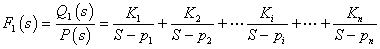
式中 ,
, ,……
,…… 是对应于
是对应于 极点
极点 的留数。留数
的留数。留数 可由下面两式求出,即:
可由下面两式求出,即:
 (式9-3-1)
(式9-3-1)
或:
 (式9-3-2)
(式9-3-2)
于是 的反变换式为:
的反变换式为:
 (式9-3-3)
(式9-3-3)
例9-3-1:求 的拉普拉斯反变换式。
的拉普拉斯反变换式。
解: 的部分分式展开式为:
的部分分式展开式为:
由(式9-3-1):

同理可得: ,
,
于是:

二、当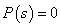 包含有共轭复根时
包含有共轭复根时
设:


当 是实系数多项式时,
是实系数多项式时, 是复数,
是复数, 是
是 的共轭复数。
的共轭复数。


例9-3-2 求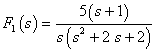 的原函数
的原函数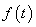 。
。
解:


由(式9-3-1):

 的原函数
的原函数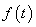 为:
为:

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
- 相关推荐
- 拉普拉斯
-
#硬声创作季 10.2.2 拉普拉斯反变换的引出Mr_haohao 2022-09-02
-
#硬声创作季 11.1.2 留数法计算拉普拉斯反变换的例子Mr_haohao 2022-09-02
-
#硬声创作季 11.1.3 留数法计算拉普拉斯反变换的注意事项Mr_haohao 2022-09-02
-
#硬声创作季 #信号 信号与系统-1.11 拉普拉斯反变换-3水管工 2022-10-31
-
[8.5.1]--单边拉普拉斯反变换jf_90840116 2022-12-11
-
电路:6.2拉普拉斯反变换(1)张峰教授(1)#电路知识学习硬声知识 2023-01-12
-
电路:6.2拉普拉斯反变换(2)张峰教授(2)#电路知识学习硬声知识 2023-01-12
-
电路:6.2拉普拉斯反变换(2)张峰教授(3)#电路知识学习硬声知识 2023-01-12
-
[5.3.1]--5.3拉普拉斯反变换jf_75936199 2023-05-31
-
拉普拉斯反变换.ppt2009-09-16 0
-
拉普拉斯变换课件教案2009-07-09 617
-
拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表2017-12-05 259654
-
数值拉普拉斯反变换求解方法2018-03-06 1101
全部0条评论

快来发表一下你的评论吧 !

