

无损长线的某些应用
电子常识
描述
一、代替电感、电容
如上所述,不同长度的无损短路线或开路线可作为电感或电容元件,用于滤波、振荡器等,请见下两例。
例10-10-1 某高频无损线,特性阻抗,波长,波速为光速,希望用该无损线代替大小为的电感,求所需长度。
解:小于的短接无损线相当于电感,由无损短路线方程:
入端阻抗为:
由于,所以:
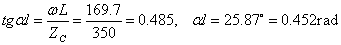
又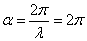 ,最后得:
,最后得:
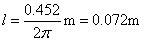
综上所述可见,将无损短路线用作电感时,求线长的公式为:
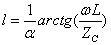 (10-10-1)
(10-10-1)
例10-10-2 上题,希望用无损线代替电容2pF,求所需长度。
解:小于的开路无损线相当于电容。输入阻抗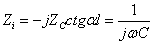 ,故线长l为:
,故线长l为:
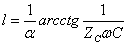 (10-10-2)
(10-10-2)
代入数据:
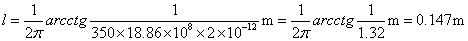
综上所述可见,将无损开路线用作电容时,求线长的公式为:
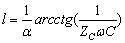
二、用作绝缘支架和仪表联线
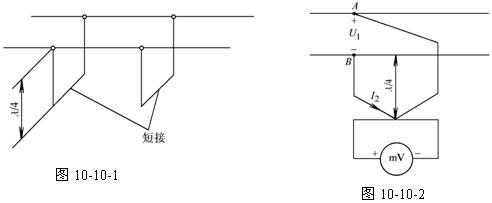
的短路无损线的输入阻抗为,输入阻抗极高,在超高频电路中可用其作为绝缘支架,如图10-10-1所示。这样可避免常规绝缘子的介质损耗。
也可利用的短接无损线测量高频线路上的电压 ,如图10-10-2所示。
,如图10-10-2所示。
三、用作阻抗变换
图10-10-3中天线的阻抗是一纯电阻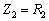 ,左方的馈电线的特性阻抗为
,左方的馈电线的特性阻抗为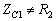 ,二者不相匹配。为此,其间串接具有特性阻抗的无损线,长度为以使从ab向右看的输入阻抗
,二者不相匹配。为此,其间串接具有特性阻抗的无损线,长度为以使从ab向右看的输入阻抗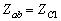 ,达到匹配的目的。
,达到匹配的目的。
由式(10-3-17)知,输入阻抗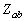 为:
为:
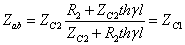
对于无损线:
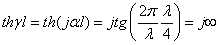
故:
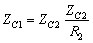
所以:
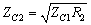 (10-10-3)
(10-10-3)
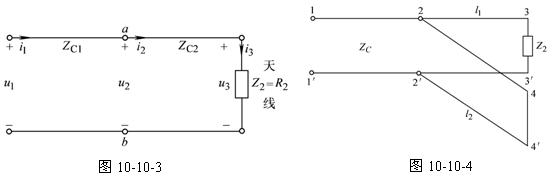
图10-10-4中上部是特性阻抗为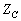 的无损线(从11′到33′),其负载阻抗为,为使达到匹配的目的,在22′处并接同样特性阻抗的无损短路线,选择l1、l2使从22′处向右看的等效并联输入阻抗为
的无损线(从11′到33′),其负载阻抗为,为使达到匹配的目的,在22′处并接同样特性阻抗的无损短路线,选择l1、l2使从22′处向右看的等效并联输入阻抗为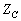 ,即:
,即:
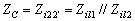 (10-10-4)
(10-10-4)
或写成:
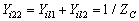 (10-10-5)
(10-10-5)
又知:
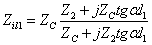 ,
, 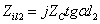
将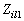 、
、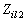 代入式(10-10-5)得:
代入式(10-10-5)得:
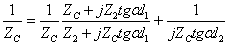 (10-10-6)
(10-10-6)
式中,已知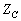 、Z2、a,由此复数方程可解出两个未知量
、Z2、a,由此复数方程可解出两个未知量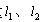 。
。
例10-10-3 图10-10-3所示线路,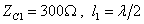 的无损线与负载不匹配,现用
的无损线与负载不匹配,现用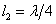 、特性阻抗的另一无损线串接其间,使之匹配,求
、特性阻抗的另一无损线串接其间,使之匹配,求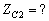 又设
又设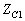 线的始端电压
线的始端电压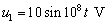 ,
,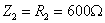 ,求。
,求。
解:为满足匹配条件,利用式(10-10-3)得:
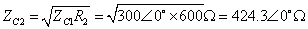 (10-10-7)
(10-10-7)
在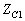 线的终端无反射,由式(10-9-5)、式(10-9-6)知:
线的终端无反射,由式(10-9-5)、式(10-9-6)知:
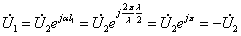 (10-10-8)
(10-10-8)
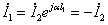 (10-10-9)
(10-10-9)
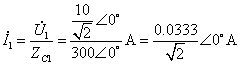
故:
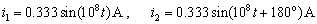
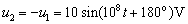
又由无损长线基本方程:
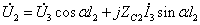
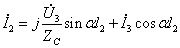
因为:
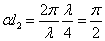
故:
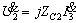
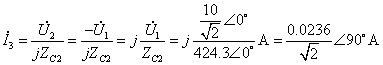
又:
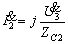
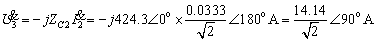
故:
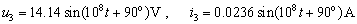
- 相关推荐
- 热点推荐
- 长线
-
音频延长线有什么用2024-10-08 1986
-
USB线如何快速延长?USB延长线太长会有影响吗?2023-11-28 7618
-
***画蛇形等长线方法分享!2019-07-23 2150
-
怎么建造一个长线夹具2019-07-01 1384
-
蛇行等长线布线方法2017-10-13 968
-
水下延长线2017-03-25 2221
-
Altium-Designer画等长线2016-07-22 1267
-
基于LabVIEW的在线式线长线径测量仪设计2016-01-04 547
-
电子元器件无损检测2015-10-23 3261
-
光耦在并口长线传输中的应用2012-08-09 2949
-
长线驱动器 ,矩阵的种类有哪些?2010-03-26 1635
-
无反射长线2009-07-27 1123
-
双通道长线传输电路2008-12-22 883
全部0条评论

快来发表一下你的评论吧 !

