

非线性正弦稳态电路
电子常识
描述
一、非线性电感中电压、电流的波形
当正弦电压施加于非线性电路时,各支路电压、电流的波形通常不再是正弦的。现考察一个非线性电感中电压和电流的波形。非线性电感一般是指具有铁芯或其他铁磁材料作为芯子的线圈,如图11-5-1a所示。设外加电压u为余弦波,略去线圈电阻和漏磁通,则由电磁感应定律可知,电压是磁链对时间的变化率:
(11-5-1)
式中,n、F、Y各为线圈匝数、磁通和磁链。从上式可求出磁通:
(11-5-2)
故磁通F是正弦波。电压有效值与磁通最大值、磁通密度最大值的关系为:
(11-5-3)
(a) (b)
图 11-5-1
式中,、S各为磁通密度最大值和铁心截面面积, (设铁心的截面各处都相同)。
(设铁心的截面各处都相同)。
利用作图法可从磁通的波形画出电流的波形。设铁心的截面面积为S,铁心长度为l,则F=BS。又根据全电流定律,磁场强度H沿闭合磁路的积分等于其链绕的电流乘线圈匝数,即:
设B和H在磁路的各处都相等,上式成为:
Hl=ni,故 (11-5-4)
F-i曲线如图11-5-1b的右上方所示。由于铁心饱和的影响,使得F-i曲线不是线性的。
下面根据已经得到的非线性电感曲线,求取F(t)= Fmsinwt时的波形。见图11-5-1,按图中箭头所示的作图路线,依次得到点a、b、c、d。其中d点是cd和ed的交点,而ed就是的值。按同样方法选取不同的时间t,可逐点作出i(t)。从图上看出,i(t)是非正弦类似地,如已知带铁心线圈曲线和线圈电流为正弦I(t)= Imsinwt,可以用作图法求取F(t)和u(t)。如图11-5-2所示。
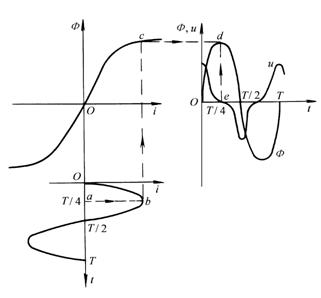
图 11-5-2
二、等效正弦波
当正弦电压施加在一个线性电阻和一个非线性电感串联的电路中时,各元件的电压、电流波形都是非正弦的,严格分析此电路是很困难的。如果电压、电流的正弦畸变不太严重时(即主要是基波,谐波分量较小),可近似地用所谓等效正弦波近似。
等效正弦波定义如下:等效正弦电压、电流的有效值各等于实际的非正弦电压、电流的有效值,等效正弦电压、电流形成的有功功率等于实际的非正弦有功功率(平均功率),即:
 (11-5-5)
(11-5-5)
 (11-5-6)
(11-5-6)
式中的下标eq表示等效正弦,故:
(11-5-7)
的正负号可根据非正弦波中基波的相位差的正负号决定。
利用等效正弦波的概念,可将非线性元件看成所谓“惯性元件”,其中的瞬时值关系是线性的,故施加正弦电压能产生正弦电流,可以用复数进行计算。
如图11-5-3所示。曲线1为钨丝灯泡的有效值特性,曲线2为热敏电阻的有效值特性。此类元件都称为惯性元件。

图 11-5-3
三、利用等效正弦波分析交流非线性电路
利用等效正弦波可使交流非线性稳态电路分析大为简化。图11-5-4a电路由线性阻抗 和非线性电感串联组成,后者即铁心线圈(忽略线圈电阻、漏感、铁心损耗等)。由外施正弦电压供电,将非线性电感看作惯性元件,进行复数计算:
和非线性电感串联组成,后者即铁心线圈(忽略线圈电阻、漏感、铁心损耗等)。由外施正弦电压供电,将非线性电感看作惯性元件,进行复数计算:
(11-5-8)
式中,是非线性电感上的等效电压复数,故超前电流90°,于是和同相。总电压有效值的平方为:
(11-5-9)
图 11-5-4
非线性电感的有效值特性如图11-5-4b所示。若已知某一外施电压有效值U,通过辅助特性曲线,找出I值和非线性电感上的电压,可求出线性阻抗Z上的电压。
- 相关推荐
- 非线性
-
正弦稳态分析2008-12-04 798
-
正弦稳态电路的分析与计算2010-04-13 838
-
正弦稳态电路的功率2010-10-08 478
-
非正弦周期信号电路的稳态计算2009-07-27 3465
-
正弦稳态电路详细解析:正弦稳态电路的定义,正弦稳态电路电路解析2017-05-05 36522
-
电路设计--正弦稳态电路习题课2017-08-07 910
-
电路设计--正弦稳态电路2017-08-07 1529
-
正弦交流电路的稳态分析2021-06-19 1037
-
电路理论的基础知识之正弦稳态电路的分析2022-01-13 1044
-
线性电路正弦稳态分析方法之相量法2023-03-09 7016
-
线性电路与非线性电路的区别是什么?2023-09-04 9186
-
非线性电路的基本特点是什么2024-07-09 1299
-
正弦振荡电路的非线性部分是什么2024-09-29 545
全部0条评论

快来发表一下你的评论吧 !

