|
为了使控制系统能可靠地工作,不但要求它能稳定,而且还希望有足够的稳定裕量,使系统在环境发生变化或存在干扰的情况下仍能工作,这即为相对稳定性的概念。
在讨论系统的稳定裕量时,首先要假定开环系统是稳定的,是最小相位系统,即开环系统的零、极点均仅位于s的左半平面,否则讨论系统的稳定裕量是无意义的。
为了说明相对稳定性的概念,图5-49为一典型的I型系统 曲线,其开环系统的传递函数为: 曲线,其开环系统的传递函数为: 。根据奈氏判据可知,当 。根据奈氏判据可知,当 时,系统不稳定,奈氏曲线包围(-1,j0)点;当 时,系统不稳定,奈氏曲线包围(-1,j0)点;当 时,系统产生等幅振荡,奈氏曲线经过(-1,j0)点;当 时,系统产生等幅振荡,奈氏曲线经过(-1,j0)点;当 时,系统稳定,奈氏曲线不包围(-1,j0)点。因此直观地看,对于开环稳定的系统,要求闭环系统有一定的稳定性,不仅要求 时,系统稳定,奈氏曲线不包围(-1,j0)点。因此直观地看,对于开环稳定的系统,要求闭环系统有一定的稳定性,不仅要求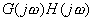 的幅频特性不包围(-1,j0)点,而且应与该点有一定的距离,即有一定的稳定裕量。 的幅频特性不包围(-1,j0)点,而且应与该点有一定的距离,即有一定的稳定裕量。
衡量闭环系统相对稳定性的具体指标有幅值裕量 和相位裕量 和相位裕量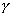 。在Matlab中,相应地有专门的函数来求取上述指标:Margin。具体用法参见下面的例子。 。在Matlab中,相应地有专门的函数来求取上述指标:Margin。具体用法参见下面的例子。
5.5.1 用奈氏图表示相位裕量和幅值裕量
1、 相位裕量
设一开环稳定的系统的奈氏曲线 负实轴相交于G点,与单位圆相交于C点,如图5-50。对应于 负实轴相交于G点,与单位圆相交于C点,如图5-50。对应于 时的频率 时的频率 (交点C)称为增益穿越频率,又称剪切频率或交界频率。在剪切频率 (交点C)称为增益穿越频率,又称剪切频率或交界频率。在剪切频率 处,使系统达到临界稳定状态时所能接受的附加相位迟后角,定义为相位裕量,用 处,使系统达到临界稳定状态时所能接受的附加相位迟后角,定义为相位裕量,用 表示之。对于任何系统,相位裕量 表示之。对于任何系统,相位裕量 的算式为 的算式为
式中, 是开环频率特性在剪切频率 是开环频率特性在剪切频率 处的相位。 处的相位。
不难理解,对于开环稳定的系统,若 ,表示 ,表示 曲线包围(-1,j0)点,相应的闭环系统是不稳定的;反之,若 ,则相应的闭环系统是稳定的。一般 曲线包围(-1,j0)点,相应的闭环系统是不稳定的;反之,若 ,则相应的闭环系统是稳定的。一般 越大,系统的相对稳定性也就越好。因为系统的参数并非绝对不变,如果 越大,系统的相对稳定性也就越好。因为系统的参数并非绝对不变,如果  太小,就有可能因参数的变化而使奈奎斯特曲线包围(-1,j0)点,即导致系统不稳定。 太小,就有可能因参数的变化而使奈奎斯特曲线包围(-1,j0)点,即导致系统不稳定。
2、 幅值裕量
幅值裕量是系统相对稳定性的另一度量指标。如图5-50所示,开环频率特性的相角 时的频率 时的频率 (交点G)处, (交点G)处, 称为相位穿越频率,又称为相位交界频率。开环幅值 称为相位穿越频率,又称为相位交界频率。开环幅值 的倒数称为增益裕量,用 的倒数称为增益裕量,用 表示。即 表示。即
上式表示系统在变到临界稳定时,系统的增益能增大多少。
由奈奎斯特稳定判据可知,对于最小相位系统,其闭环稳定的充要条件是 曲线不包围(-1,j0)点,即 曲线不包围(-1,j0)点,即 曲线与其负实轴交点处的模小于1,此时对应的 曲线与其负实轴交点处的模小于1,此时对应的 。反之,对于不稳定的系统,其 ,如图5-51所示,闭环系统是不稳定的。 。反之,对于不稳定的系统,其 ,如图5-51所示,闭环系统是不稳定的。
5.5.2 用伯德图表示相位裕量和幅值裕量
上述的相位裕量和幅值裕量也可在对数幅相图(Bode图)上表示。对应于图5-50,其Bode图如图5-52所示。图5-50中的增益穿越频率 对应于图5-52的零分贝线上的点,即开环对数幅频特性曲线与 对应于图5-52的零分贝线上的点,即开环对数幅频特性曲线与 轴的交点;图5-50中相位穿越频率 轴的交点;图5-50中相位穿越频率 的点在Bode图上是对应相角 的点在Bode图上是对应相角 的点,即相频曲线与 的点,即相频曲线与 水平线的交点。从图5-50可见,相频特性曲线上对应于增益穿越频率 水平线的交点。从图5-50可见,相频特性曲线上对应于增益穿越频率 的点位于 的点位于 水平线的上方。 水平线的上方。
在Bode图上,增益裕量常用分贝数表示,即
上式表示系统在到达临界稳定前,允许系统增益增大的倍数。对于稳定的系统,由于 <1,即 <1,即 为负,由式(5-56)可知,增益裕量为正,这时对数幅频特性曲线上对应 为负,由式(5-56)可知,增益裕量为正,这时对数幅频特性曲线上对应 的点在 的点在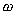 轴下方,如图5-52;当系统不稳定时,相应地,可将图5-51绘制在Bode图上,如图5-53,这时相位裕量和幅值裕量均是负的。 轴下方,如图5-52;当系统不稳定时,相应地,可将图5-51绘制在Bode图上,如图5-53,这时相位裕量和幅值裕量均是负的。
增益裕量和相位裕量通常作为设计控制系统的频域性能指标。大的增益裕量和相位裕量表明控制系统是非常稳定的,但此时控制系统的响应速度将是非常慢的,而当增益裕量接近1或相位裕量接近零时,则对应一个高度振荡的系统。因此从工程的角度出发,一般控制系统设计时采用如下的裕量范围是比较合适的: 在 在 到 到 之间,增益裕量大于6dB。 之间,增益裕量大于6dB。
同时需要指出,单独使用增益裕量或相位裕量作性能分析,都不足以说明系统的相对稳定性,必须同时给出这两个稳定裕量。对于大多数控制系统来说,这两个指标是统一的,但有时情况并非如此,图5-54a、图5-54b分别表示了这两种情况下的频率特性。
图5-54 开环控制系统的奈氏图
(a) 好的幅值裕量和差的相角裕量
(b) 好的相角裕量和差的幅值裕量
|
例5-10 试求:(1)K=1时系统的相位裕量和增益裕量。(2)要求通过增益K的调整,使系统的增益裕量 ,相位裕量 。 ,相位裕量 。
例5-10 试求:(1)K=1时系统的相位裕量和增益裕量。(2)要求通过增益K的调整,使系统的增益裕量 ,相位裕量 。 ,相位裕量 。
已知一单位反馈系统的开环传递函数为
解 (1)基于在 处的开环频率特性的相角为 处的开环频率特性的相角为
即
由三角函数的性质,有
求得 。 。
同时,在  处的开环对数幅值为 处的开环对数幅值为
则
根据K=1时的开环系统传递函数,可知系统的 ,从而 ,从而
此小题也可用Matlab直接求解。
g=tf(1,conv([1,0],conv([0.2,1],[0.05,1])))
Transfer function:
1
-----------------------
0.01 s^3 + 0.25 s^2 + s
margin(g)
(2)由题意得 ,即 。在 处的对数幅值为 ,即 。在 处的对数幅值为
上式简化后为
解之得,K=2.5。
根据 的要求,则得
即
利用三角函数的性质,可求得 。于是有
即
求解上式得 。不难看出,K取2.5就能同时满足 和 的要求。
5.5.3 对数幅频特性中频段与系统动态性能的关系
在分析控制系统的开环对数幅相频率特性时,习惯上将频率范围分为三个频段:低频段、中频段和高频段。其中低频段反映了控制系统的静态特性,关于此点在5.3.4中我们作了分析;中频段则反映了系统的动态特性,这是控制设计中一个非常关心的问题,这将在下面作介绍;高频段则主要反映了系统的抗干扰能力,对动态性能影响不大,将不作介绍。
中频段的主要参数有:剪切频率 、相位裕量 和中频宽度h。对于图5-56所示系统,其中频宽度一般定义在斜率等于 、靠近 处:
一般要求最小相位系统的开环对数幅频特性在 处的斜率等于 。如果在该处的斜率等于或小于为 ,则对应的系统可能不稳定,或者系统即使稳定,但因相位裕量较小,系统的稳定性也较差。下面通过二阶系统和三阶系统对上述结论进行说明。
设一标准二阶系统的开环传递函数为:
式中,自然振荡频率 ,阻尼比 ,其中 为转角频率,则: ,阻尼比 ,其中 为转角频率,则:
(1) 当 时, ,如图5-57a示,阶跃响应是衰减较慢的振荡过程;
(2) 当 时, ,如图5-57b示,阶跃响应是衰减较快的振荡过程;
(3) 当 时, ,如图5-57c示,阶跃响应是接近无振荡的非周期过程;
再设一个三阶系统的开环传函数为:
取K=0.1,1,10,100,得到如图5-58的幅频曲线a,b,c,d。由图可见。当 时,式(5-59)的对数幅频特性曲线如图5-58所示的曲线 。剪切频率 在斜率为 的区段内,对照图5-58下部的相频特性曲线可知,相位裕量为 ,因此闭环系统是稳定的。若开环放大系数K值减小,则对数幅频特性曲线向下垂直移动。这时剪切频率 向左移动[注意,K变化时,系统的相频特性曲线 不变。由图5-58可知,相位裕量 将增大。当剪切频率 移至斜率为 的区段内时,相位裕量 将更大,如图5-58的曲线b所示。反之,增大开环放大系数K,剪切频率 将向右移动,相位裕量 将减小,当 移至 时( 为相位穿越频率), ,闭环系统处于临界稳定。当 时, ,这时对数幅频特性曲线的中频段斜率仍为 ,如图5-58曲线c所示。因这时 为负值,所以闭环系统已不稳定了。如果开环放大系数K继续加大,使剪切频率 ,如图5-58曲线c所示。因这时 为负值,所以闭环系统已不稳定了。如果开环放大系数K继续加大,使剪切频率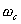 落在对数幅频特性曲线斜率为 落在对数幅频特性曲线斜率为 的区段内,如图5-58曲线b所示。这时相位裕量 的区段内,如图5-58曲线b所示。这时相位裕量 “负”得更历害,系统将更加不稳定。 “负”得更历害,系统将更加不稳定。
根据上述分析,可得到如下结论:为使闭环系统稳定且系统的阶跃响应无超调量或或超调很小,应使剪切频率 位于斜率为 位于斜率为 的线段上,同时要有一定的中频宽度,中频段越宽,则阶跃响应越接近非周期过程。 的线段上,同时要有一定的中频宽度,中频段越宽,则阶跃响应越接近非周期过程。 | 




 曲线,其开环系统的传递函数为:
曲线,其开环系统的传递函数为: 。根据奈氏判据可知,当
。根据奈氏判据可知,当 时,系统不稳定,奈氏曲线包围(-1,j0)点;当
时,系统不稳定,奈氏曲线包围(-1,j0)点;当 时,系统产生等幅振荡,奈氏曲线经过(-1,j0)点;当
时,系统产生等幅振荡,奈氏曲线经过(-1,j0)点;当 时,系统稳定,奈氏曲线不包围(-1,j0)点。因此直观地看,对于开环稳定的系统,要求闭环系统有一定的稳定性,不仅要求
时,系统稳定,奈氏曲线不包围(-1,j0)点。因此直观地看,对于开环稳定的系统,要求闭环系统有一定的稳定性,不仅要求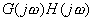 的幅频特性不包围(-1,j0)点,而且应与该点有一定的距离,即有一定的稳定裕量。
的幅频特性不包围(-1,j0)点,而且应与该点有一定的距离,即有一定的稳定裕量。 和相位裕量
和相位裕量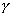 。在Matlab中,相应地有专门的函数来求取上述指标:Margin。具体用法参见下面的例子。
。在Matlab中,相应地有专门的函数来求取上述指标:Margin。具体用法参见下面的例子。 负实轴相交于G点,与单位圆相交于C点,如图5-50。对应于
负实轴相交于G点,与单位圆相交于C点,如图5-50。对应于 时的频率
时的频率 (交点C)称为增益穿越频率,又称剪切频率或交界频率。在剪切频率
(交点C)称为增益穿越频率,又称剪切频率或交界频率。在剪切频率 表示之。对于任何系统,相位裕量
表示之。对于任何系统,相位裕量
 是开环频率特性在剪切频率
是开环频率特性在剪切频率 处的相位。
处的相位。
 ,表示
,表示 曲线包围(-1,j0)点,相应的闭环系统是不稳定的;反之,若 ,则相应的闭环系统是稳定的。一般
曲线包围(-1,j0)点,相应的闭环系统是不稳定的;反之,若 ,则相应的闭环系统是稳定的。一般 越大,系统的相对稳定性也就越好。因为系统的参数并非绝对不变,如果
越大,系统的相对稳定性也就越好。因为系统的参数并非绝对不变,如果  时的频率
时的频率 (交点G)处,
(交点G)处, 的倒数称为增益裕量,用
的倒数称为增益裕量,用 表示。即
表示。即
 曲线不包围(-1,j0)点,即
曲线不包围(-1,j0)点,即 。反之,对于不稳定的系统,其 ,如图5-51所示,闭环系统是不稳定的。
。反之,对于不稳定的系统,其 ,如图5-51所示,闭环系统是不稳定的。
 对应于图5-52的零分贝线上的点,即开环对数幅频特性曲线与
对应于图5-52的零分贝线上的点,即开环对数幅频特性曲线与 轴的交点;图5-50中相位穿越频率
轴的交点;图5-50中相位穿越频率 的点在Bode图上是对应相角
的点在Bode图上是对应相角 的点,即相频曲线与
的点,即相频曲线与

 <1,即
<1,即 为负,由式(5-56)可知,增益裕量为正,这时对数幅频特性曲线上对应
为负,由式(5-56)可知,增益裕量为正,这时对数幅频特性曲线上对应 的点在
的点在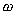 轴下方,如图5-52;当系统不稳定时,相应地,可将图5-51绘制在Bode图上,如图5-53,这时相位裕量和幅值裕量均是负的。
轴下方,如图5-52;当系统不稳定时,相应地,可将图5-51绘制在Bode图上,如图5-53,这时相位裕量和幅值裕量均是负的。 在
在 到
到 之间,增益裕量大于6dB。
之间,增益裕量大于6dB。
 ,相位裕量 。
,相位裕量 。
 处的开环频率特性的相角为
处的开环频率特性的相角为

 。
。 处的开环对数幅值为
处的开环对数幅值为
 ,从而
,从而
 ,即 。在 处的对数幅值为
,即 。在 处的对数幅值为

 ,阻尼比 ,其中 为转角频率,则:
,阻尼比 ,其中 为转角频率,则: ,如图5-58曲线c所示。因这时 为负值,所以闭环系统已不稳定了。如果开环放大系数K继续加大,使剪切频率
,如图5-58曲线c所示。因这时 为负值,所以闭环系统已不稳定了。如果开环放大系数K继续加大,使剪切频率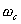 落在对数幅频特性曲线斜率为
落在对数幅频特性曲线斜率为 的区段内,如图5-58曲线b所示。这时相位裕量
的区段内,如图5-58曲线b所示。这时相位裕量 “负”得更历害,系统将更加不稳定。
“负”得更历害,系统将更加不稳定。
 位于斜率为
位于斜率为 的线段上,同时要有一定的中频宽度,中频段越宽,则阶跃响应越接近非周期过程。
的线段上,同时要有一定的中频宽度,中频段越宽,则阶跃响应越接近非周期过程。