

晶体学基础
机械设计
描述
2.1.1 空间点阵和晶胞
?具有代表性的基本单元(最小平行六面体)作为点阵的组成单元,称为晶胞。将晶胞作三维的重复堆砌就构成了空间点阵。
为了便于分析研究晶体中质点的排列规律性,可先将实际晶体结构看成完整无缺的理想晶体并简化,将其中每个质点抽象为规则排列于空间的几何点,称之为阵点。这些阵点在空间呈周期性规则排列并具有完全相同的周围环境,这种由它们在三维空间规则排列的阵列称为空间点阵,简称点阵。同一空间点阵可因选取方式不同而得到不相同的晶胞
晶胞、晶轴和点阵矢量
根据6个点阵参数间的相互关系,可将全部空间点阵归属于7种类型,即7个晶系。按照"每个阵点的周围环境相同"的要求,布拉菲(Bravais A.)用数学方法推导出能够反映空间点阵全部特征的单位平面六面体只有14种,这14种空间点阵也称布拉菲点阵。
|
布拉非点阵 |
晶系 |
布拉非点阵 |
晶系 |
|
简单三斜 |
三斜 |
简单六方 |
六方 |
|
简单单斜 |
单斜 |
简单菱方 |
菱方 |
|
简单正交 |
正交 |
简单四方 |
四方 |
|
简单立方 |
立方 |
2.1.2 晶向指数和晶面指数
为了便于确定和区别晶体中不同方位的晶向和晶面,国际上通用密勒(Miller)指数来统一标定晶
向指数与晶面指数。
1.晶向指数 
图2.6?正交晶系一些重要晶向的晶向指数
晶向指数的确定步骤如下:
1)以晶胞的某一阵点O为原点,过原点O的晶轴为坐标轴x,y, z, 以晶胞点阵矢量的长度作为坐标轴的长度单位。
2)过原点O作一直线OP,使其平行于待定晶向。
3)在直线OP上选取距原点O最近的一个阵点P,确定P点的3个坐标值。
4)将这3个坐标值化为最小整数u,v,w,加以方括号,[u v w]即为待定晶向的晶向指数。
2.晶面指数

图2.7?正交点阵中一些晶面的面指数
?晶面指数标定步骤如下:
1)在点阵中设定参考坐标系,设置方法与确定晶向指数时相同;
2)求得待定晶面在三个晶轴上的截距,若该晶面与某轴平行,则在此轴上截距为无穷大;若该晶面与某轴负方向相截,则在此轴上截距为一负值;
3)取各截距的倒数;
4)将三倒数化为互质的整数比,并加上圆括号,即表示该晶面的指数,记为( h k l )。
?晶面指数所代表的不仅是某一晶面,而是代表着一组相互平行的晶面。另外,在晶体内凡晶面间距和晶面上原子的分布完全相同,只是空间位向不同的晶面可以归并为同一晶面族,以{h k l}表示,它代表由对称性相联系的若干组等效晶面的总和。
3.六方晶系指数
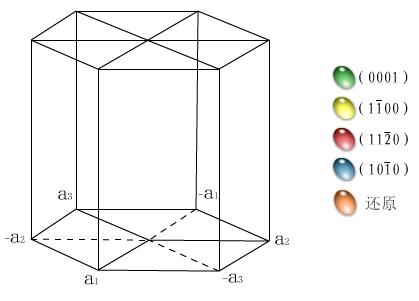
图2.8 六方晶系一些晶面的指数
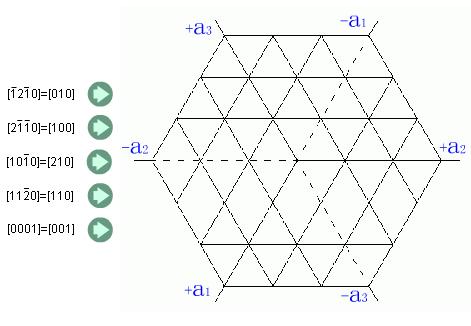
图2.9 六方晶系晶像指数的表示方法(c轴与图面垂直)
六方晶系的晶向指数和晶面指数同样可以应用上述方法标定,这时取a1,a2,c为晶轴,而a1轴与a2轴的夹角为120度,c轴与a1,a2轴相垂直,如图2.13所示。但这种方法标定的晶面指数和晶向指数,不能完全显示六方晶系的对称性,为了更好地表达其对称性,根据六方晶系的对称特点,对六方晶系采用a1,a2,a3及c四个晶轴,a1,a2,a3之间的夹角均为120度,这样,其晶面指数就以(h k i l)四个指数来表示。
根据几何学可知,三维空间独立的坐标轴最多不超过三个。前三个指数中只有两个是独立的,它们之间存在以下关系:i =- ( h + k ) 。
采用4轴坐标时,晶向指数的确定原则仍同前述(见图2.14),晶向指数可用{u v t w}来表示,这里 u + v = - t。
4.晶带
?所有平行或相交于同一直线的这些晶面构成一个晶轴,此直线称为晶带轴。属此晶带的晶面称为晶带面。
?晶带轴[u v w]与该晶带的晶面(h k l)之间存在以下关系: hu + kv + lw = 0
?凡满足此关系的晶面都属于以[u v w]为晶带轴的晶带,故此关系式也称作晶带定律。
5.晶面间距
图2.10 晶面间距
图2.11 晶面间距公式的推导
?由晶面指数还可求出面间距dhkl。通常,低指数的面间距较大,而高指数的晶面间距则较小。
2.1.3 晶体的对称性
1.对称元素
?晶体的对称元素可分为宏观和微观两类。宏观对称元素反映出晶体外形和其宏观性质的
?对称性。而微观对称元素与宏观对称元素配合运用就能反映出晶体中原子排列的对称性。
?a.宏观对称元素;
1)回转对称轴:当晶体绕某一轴回转而能完全复原时,此轴即为回转对称轴。注意该轴线定要通过晶格单元的几何中心,且位于该几何中心与角顶或棱边的中心或面心的连线上。在回转一周的过程中,晶体能复原n次,就称为n次对称轴。
2)对称面:晶体通过某一平面作镜像反映而能复原,则该平面称为对称面或镜面。
3)对称中心:晶体通过某一平面作镜像反映而能复原,则该平面称为对称面或镜面。
4)回转-反演轴:若晶体绕某一轴回转一定角度(360/n),再以轴上的一个中心点作反演之后能得到复原时,此轴称为回转-反演轴。
图2.12 对称轴
图2.13 对称面
图2.14 对称中心
图2.15 回转-反演轴
?b.微观对称元素;
??(1)滑动面。
??? 一个对称面加上沿着此面的平移所组成,晶体结构可借此面的反映并沿此面平移
??? 一段距离而复原。
??(2)螺旋轴。
??? 回转轴和平行于轴的平移所构成。
2.32种点群
?点群是指一个晶体中所有点对称元素的集合。点群在宏观上表现为晶体外形的对称。利
?用组合定理可导出晶体外形中只能有32种对称点群。
2.1.4 极射投影
1.极射投影原理
极射投影的原理如图2.23所示。先在参考球中选定一条过球心的直线AB(直线),过A点作一平面与参考球相切,该平面即为投影面,也称极射面。若球面上有一极点P,连接BP并延长之,使其与投影面相交于P',P'即为极点P在投影面上的极射投影。过球心作一平面N'E'S'W'与AB垂直(与投影面平行),它在球面上形成一个直径与球径相等的圆称大圆。大圆在投影面上的投影为N'E'S'W'也是一个圆,称为基圆。所有位于左半球球面上的极点,投影后的极射投影点均将落在基圆之内。然后将投影面移至B点,并以A点为投影点,将所有位于右半球球面上的极点投射到位于B处的投影面上,并冠以负号。最后将A处和B处的极射投影图重叠地画在一张图上。这样,球面上所有可能出现的极点,都可以包括在同一张极射投影图上。
2.吴氏(WulFF)网
图2.16 吴氏网(分度为2°)
3.标准投影

图2.17 立方晶体详细的(001)标准投影图
以晶体的某个晶面平行于投影面上作出全部主要晶面的极射投影图称为标准投影。一般选择一些重要的低指数的晶面作为投影面,这样得到的图形能反映晶体的对称性。立方晶系常用的投影面是( 001 ),( 110 ) 和( 111 );六方晶系则为( 0001 )。立方晶系的( 001 )标准投影如上图所示。
-
2011-05-13
7 回复 举报收起回复
- 相关推荐
- 热点推荐
- 晶体学
-
《炬丰科技-半导体工艺》GaN晶体蚀刻的几何方面和光子应用2021-07-08 3488
-
关于氮化镓的晶体学湿式化学蚀刻的研究2022-01-17 2065
-
p型氮化镓的晶体学湿式化学蚀刻2023-03-22 2849
-
如何表达晶体取向?介绍一下晶体取向的图形表示法2023-10-08 11684
-
氮化镓的晶体学湿式化学蚀刻法2023-11-24 2088
-
电子背散射衍射(EBSD):揭示材料晶体学信息的窗口2024-11-18 2101
-
电子背散射衍射晶体学织构分析与数据处理2025-01-07 1598
-
晶体结构中晶面和晶向的关系2025-06-05 2974
-
材料的晶体结构看不清?EBSD助您获取关键数据2025-09-30 719
全部0条评论

快来发表一下你的评论吧 !

