1024QAM调制中EVM要小于多少才能正常通信？

移动通信技术对数据传输速率要求越来越高。一种提高传输速率的思路是使用更高阶的QAM 调制方式，例如5G NR 的256QAM PDSCH，微波的1024QAM，2048QAM和4096QAM 调制。更高阶的QAM 调制方式对系统也提出了更高的要求。例如某个系统的EVM 测试结果为3%，这个EVM 算好还是不好，单纯从数值看似乎很好，但是EVM 的好坏与否不仅要看数值，还要看其调制阶数，不同调制阶数对EVM要求不同。直观来看，更高阶QAM 调制方式对EVM 有更高要求，但是具体要求是多少？例如对1024QAM 调制，EVM 要小于多少才能实现正常通信？本文主要讨论这个问题。EVM确定了，就可以指导系统信噪比SNR（SIGNAL NOISE RATIO）的指标分解和预算。

例如3GPP  TS38.141对5G  NR 不同调制方式的PDSCH EVM 要求如下表，从表中也可以看到随着调制阶数的提高，EVM 的要求在不断提高，这些EVM 是怎么定出来的？目前已经有客户开始测试1024QAM 的PDSCH，TS38.141 没有给出1024QAM 的EVM 要求，在测试的时候1024QAM EVM多少才算通过？本文将会给出答案。

表1、TS38.141对不同阶QAM EVM指标要求

 

Modulation scheme for PDSCH	Required EVM (%)
QPSK	18.50%
16QAM	13.50%
64QAM	9%
256QAM	4.50%

 

1、QAM 调制及EVM 以及EVM 与SNR 的关系

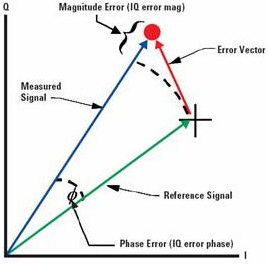
图1、EVM定义

QAM 调制信号通常用其EVM 来衡量信号质量，EVM是英文Error Vector Magnitude缩写，意为误差向量幅度，其定义为误差矢量Error Vector 的幅度与参考信号Reference Signal 幅度的比值，有时候用百分比比表示，有时候用dB 表示。通常测量的EVM为其RMS 值，计算公式如下：

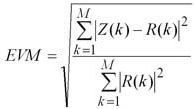
EVM 可以与信噪比SNR 相互换算，在星座图中，EVM 是以电压表示的，因而二者之间的换算公式如下，当然如果有编码增益，要在该公式中考虑编码增益，例如扩频增益。

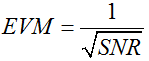
2、不同阶QAM 信号对EVM 的要求

不同阶QAM 对信号的抗干扰能力是不一样的，数字调制信号调制方式越复杂，频率带宽利用率越高，调制方式越复杂，抗干扰能力越差，功率利用率低，也就是说接收时需要较高的C/N比，才能达到相同传输质量，选择调制方式需要根据通信系统在这两个方面折衷256QAM 的符号点间距离比BPSK 调制近的多，这意味256QAM 和BPSK 相比容易被干扰而造成误码。

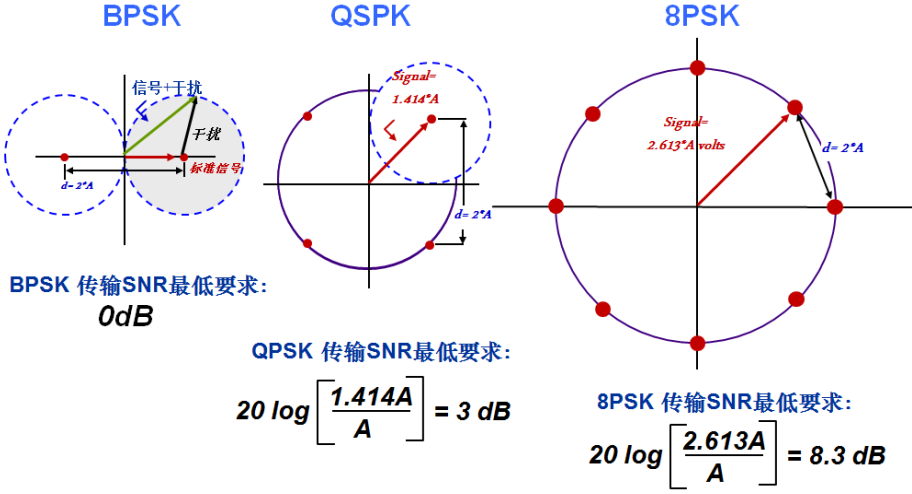
图2、不同调制方式抗干扰能力

从EVM 的含义看，结合几种调制方式的星座图拿来看，如果要保证通信正常，也就是星座点不发生误判，则要求每个星座点的误差矢量幅度最大为0.5a（其中a 为相邻星座点之间的间距），即|E|max<0.5a，因而每个星座点需要落在以参考信号为中心，半径为0.5a 的圆内。由于不同星座点的参考信号幅度是不一样的，离原点最远的那个星座点对应的参考信号幅度最大，记为|R|max，则其可容忍的EVM 最小，即EVM_thre=0.5a/|R|max，只要所有星座点的EVM小于EVM_thre，就不会发生误判，即总的EVM 小于EVM_thre。下图中的A=0.5a，表示相邻星座点间距的一半。

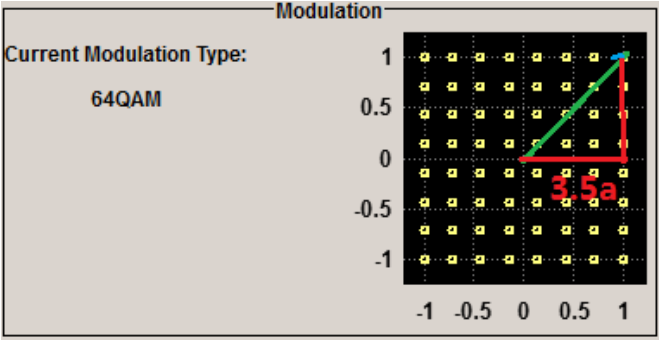
图3、64QAM EVM_thre 示意图

比如64QAM，星座图可以看作是间距为a 的8x8 阵列，那么距离原点最远的那个星座点坐标就是（3.5a,3.5a），矢量长度为1.414x3.5a，为了不发生误判，允许的矢量误差要小于半个星座间距（0.5a），这时的EVM<0.5a/(1.414x3.5a)=10.10%，为了保证接收机正常解调，留有一定的余量，5G NR 协议TS38.141 将64QAM 的EVM 限值设定在9%，是合理的。

当然这种估算方法保证了所有星座点的都不会发生误判，由于距离原点近一点的星座点参考信号幅度会小些，其EVM 会大些也不会发生误判，假设所有星座点同时达到最大误差矢量|E|max=0.5a，同时所有星座点等概率出现，此时系统的EVM 达到容忍上限，EVM 再大就会误判。此时系统的EVM RMS 值成为EVMRMS_thre，只要EVM 小于改值EVMRMS_thre，则系统一定不会发生误判。

图4、计算不同QAM 调制方式下对系统EVM 和SNR 要求门限

通过图4 Matlab 代码就可以计算出EVMRMS_thre 和EVM_thre，并计算出了其对系统SNR 的要求值。不同调制方式下对系统要求的EVM 和SNR 门限如表2 所示。从表中可看出，调制阶数越高，对系统的EVM 和SNR 要求就越高。

表2、不同QAM 调制方式对系统EVM 和SNR 要求

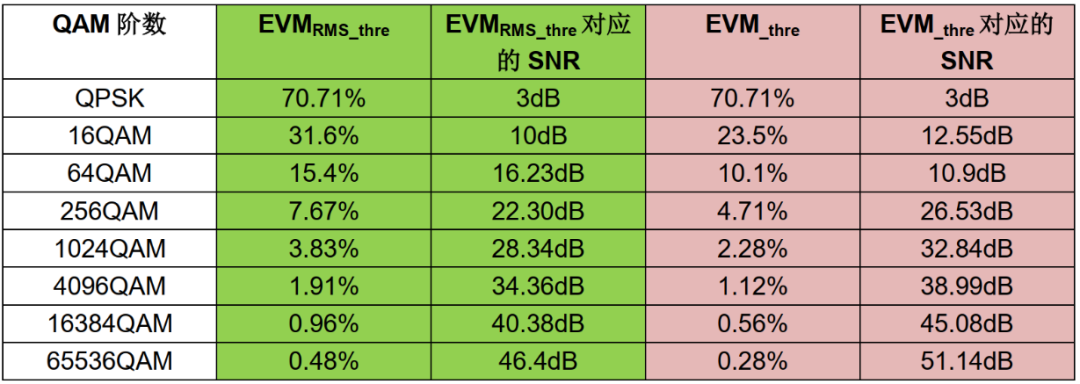
以目前已经使用的最高调制阶数4096QAM 为例，其对系统的EVM 的RMS值要求小于1.91%，如果以最远点计算EVM 要求小于1.12%。如果将信号源和频谱仪直接相连，相当于在没有衰落的静态信道条件下，EVM RMS 值最好一般在0.2%左右，所以4096QAM 对EVM 的要求已经接近于硬件的极限水平。

3、实验验证

使用信号源产生一个4096QAM 信号，使用频谱分析仪进行解调。

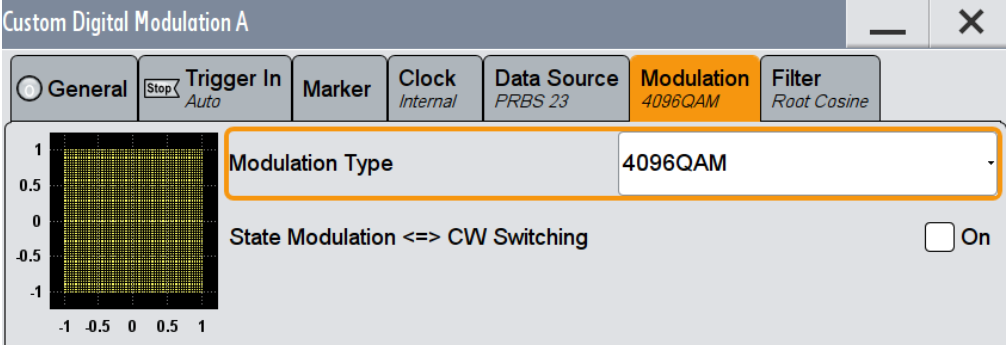
图5、生成4096QAM 调制信号

在不额外增加噪声的条件下，FSW 的解调结果如图6，其EVM 很好，星座图清晰可见。

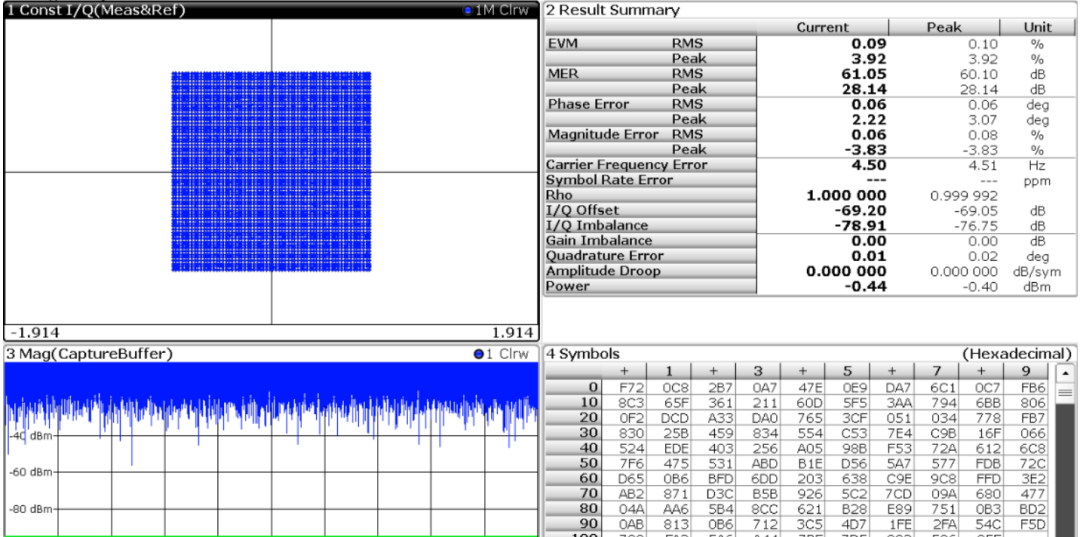
图6、不加噪声下FSW 对4096QAM 信号解调结果

根据表1 计算结果，4096QAM 对系统的EVM 要求必须小于1.91%，对应的SNR 为34.36dB。在上述信号基础上增加-34dB 的AWGN 噪声，此时加噪声后信号的解调结果如图8 所示，星座图已经接近于模糊和误判，对应的EVM 测试结果为1.56%，与理论计算1.91%还是比较接近。

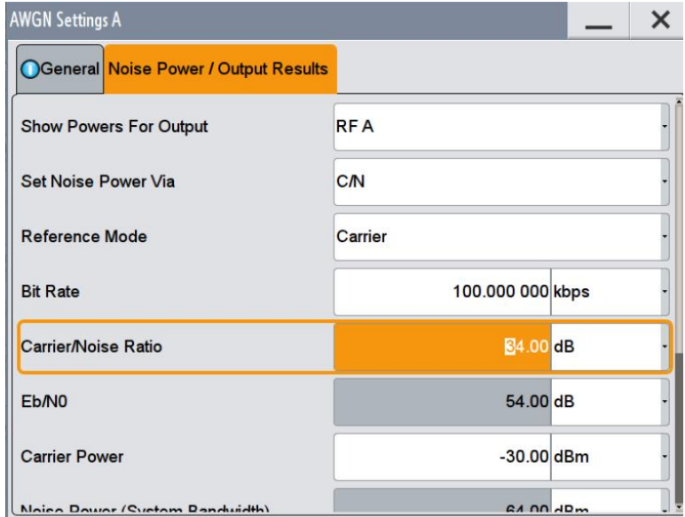
图7、4096QAM 信号增加-34dB 的AWGN 噪声

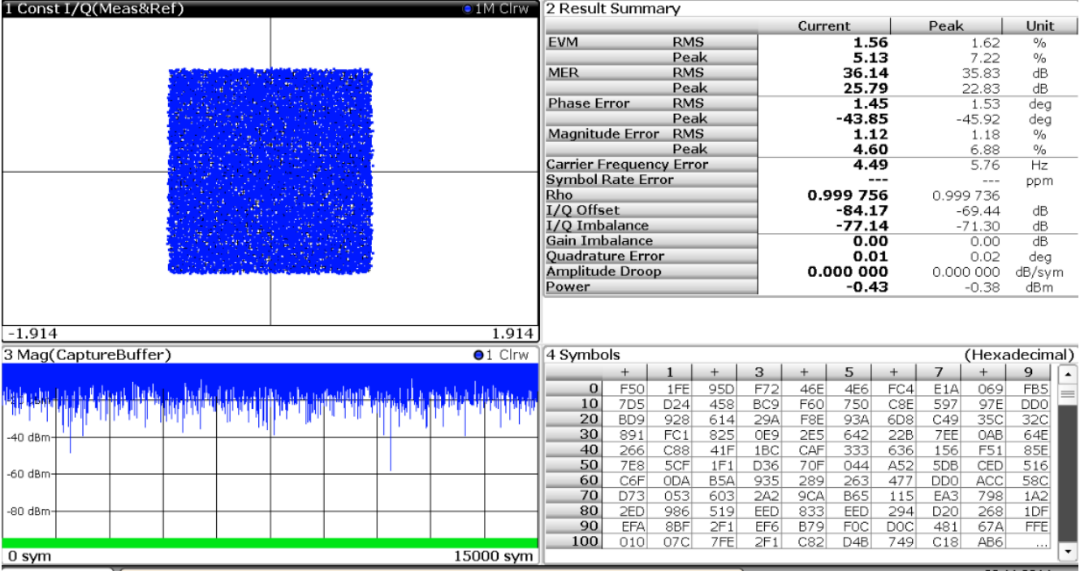
图8、加-34dB 噪声下FSW 对4096QAM 信号解调结果

4、结论

更高阶的QAM 调制方式对系统EVM 和SNR 提出了更高的要求，系统的EVM 测试结果算好还是不好，不能只单纯看EVM 数值，还要看其调制阶数。本文计算了不同调制阶数下星座点不发生误判时对系统的EVM 和SNR 要求，具体结果参考表2，该结论可以理解调制阶数与EVM的关系以及对系统SNR的要求，可以用来指导系统设计和器件选型。

 

原文标题：5G NR调制阶数与EVM关系以及对系统SNR要求分析

文章出处：【微信公众号：微波射频网】欢迎添加关注！文章转载请注明出处。

责任编辑：haq