

并联机器人的性能指标有哪些
机器人
描述
并联机器人的性能指标有哪些
并联机器人机构综合设计是一个复杂而困难的问题。机构性能指标是这些问题的关键,主要包括:奇异位形,工作空间,各向同性与灵活度,力传递性能,刚度,速度与加速度等。
奇异位形是机构的固有性质,可通过雅可比矩阵行列式为零的条件求得。此时机构无速度反解或关节驱动力无穷大,在机构设计及轨迹规划中应当避免。并联机器人的特殊构型使得奇异分析相对较易。工作空间指机器人末端执行器的工作区域,通常存在可达工作空间和灵活工作空间。
并联机构的工作空间求解依赖其运动方程,可利用的数值方法有网格法、雅可比法、蒙特卡洛法等。而并联机器人的特殊构型使其解析解较为直观。采用了几何图形交集的方法求得并联机器人的工作空间。刘辛军等采用解空间的物理模型法求解并联机器人工作空间,并逐步将这种方法发展成为了一种性能图谱理论。
灵活度用来衡量机构输入与输出运动之间的传递关系的失真程度:当机构接近奇异形位时存在病态雅可比矩阵,此时的逆矩阵精度降低;当雅可比矩阵的条件数为1时,机构处于最佳运动性能,称为运动学各向同性。目前,采用条件数来衡量各项同性和灵活度在并联机器人中已成为常用方法。
力传递性能反映并联机器人执行器上的广义力与关节驱动力之间的关系,有力椭球、条件数、传递角与传递系数等指标。力椭球建立在雅可比矩阵奇异值分解的基础上,条件数指标以雅可比矩阵最大和最小奇异值比值来反映力传递各向异性,传递角定义为刚体受力时力作用线与作用点之间的夹角。力传递性能的研究重点均是围绕评价指标与机构尺寸之间关系展开的。
刚度与机构拓扑类型、尺度、截面参数密切相关,包括静刚度和动刚度。静刚度基于静刚度解析模型来评价,动刚度衡量结构抵抗预定动态激扰能力的特性。目前有关并联机器人的动刚度报道还较少,主要借鉴其他各类机械系统的分析,采用固有频率作为衡量指标来评价,并且刚度矩阵的条件数也常用于评价局部动力学性能。
并联机器人自由度计算
在分析并联机构自由度的时候发现了问题,经过一天的学习终于得到解决,本文将通俗地介绍如何计算并联机构的自由度。
以下是我的并联机器人结构简图,是一个R-R-R-R-R-R-R-R机构。
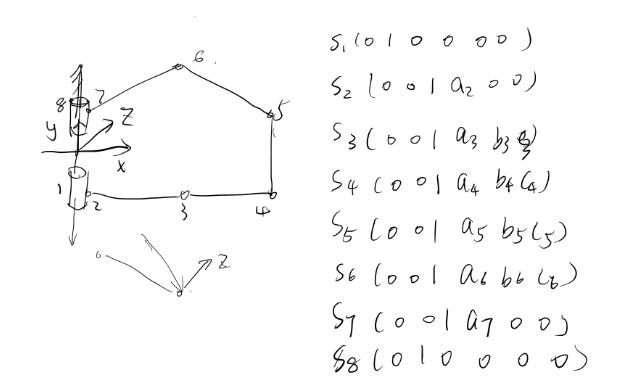
Si中前三个数字是其转轴的方向s,后三个数字是原点指向关节的向量rxs
通过求其矩阵的秩可以得到共有约束的个数为满秩-所求得的秩,即共有约束。
通过公式
F=d(n-g-1)+fi=(6-3)*(8-8-1)+8=5
责任编辑:YYX
-
并联机器人快速准确拾取物体2016-09-14 20097
-
任意波形发生器(AFG)相关性能指标有哪些?2021-04-09 1546
-
RTC的主要性能指标有哪些2021-07-22 2760
-
计算机控制系统的性能指标有哪些2021-10-25 2166
-
电容的性能指标2008-12-13 4652
-
频率响应法-- 频域性能指标和时域性能指标的关系2009-07-27 13565
-
功率放大器的性能指标有哪些?2010-04-01 19725
-
检测系统的性能指标2011-03-13 1115
-
并联机器人的特点及其运动模拟器等相关设计的介绍2017-10-17 1638
-
cpu主要技术性能指标有哪些2020-05-15 15523
-
并联机器人控制2021-04-20 971
-
电缆性能指标测试方法2021-06-22 1236
-
并联机器人和串联机器人的区别是什么?2024-01-26 5868
-
工控主板的性能指标有哪些?2024-05-10 1850
-
放大电路的性能指标有哪些2024-07-30 4577
全部0条评论

快来发表一下你的评论吧 !

