Ceph最新的EC-CLAY插件调研

Ceph对象存储方案 2021-01-03 2097

Ceph对象存储方案

5 文章 1.7w阅读 0粉丝

描述

CLAY 简介

Clay Codes ( Clay Codes: Moulding MDS Codes to Yield an MSR Code ) 是FAST18 上提出的一种编码方法，文章地址，Clay 码能够将一般的MDS 码（最优容错）转化为具有最优修复的编码方法，具有以下性质：

Minimum Storage （最小存储开销，同经典RS码和最小存储再生码，MSR）
Maximum Failure Tolerance（最大容错，即 (n,k)-Clay 码可以容任意n-k 失效）
Optimal Repair Bandwidth （最优修复开销，能够达到理论最优值）
All-Node Optimal Repair （最小开销修复所有节点的数据，包括原始数据和校验数据）
Disk Read Optimal （最优磁盘读）
Low Sub-packetization （低分包数，即码字长度短）

参考资料1//blog.foool.net/2018/05/clay-codes-%E4%BB%8E%E7%94%9F%E6%88%90%E7%9F%A9%E9%98%B5%E7%9A%84%E8%A7%92%E5%BA%A6%E6%9D%A5%E7%9C%8B/

参考资料2//blog.acolyer.org/2018/03/01/clay-codes-moulding-mds-codes-to-yield-an-msr-code/

从ceph官方的介绍,可以确认以下几点：

  • 向下兼容:CLAY插件与jerasure、ISA、SHEC插件兼容,这里可以理解为Clay是在这几个插件的基础上做的一层更高层面的数据组成抽象，能够更加细致的控制数据的分布粒度，从而实现对原有的几个插件在数据恢复场景下的性能优化。这也就是是上面提到的“Clay 码能够将一般的MDS 码（最优容错）转化为具有最优修复的编码方法”。

  • 修复性能优化"在底层已有的jerasure、ISA、SHEC几个的插件基础上，做了编码优化，能够在异常发生，需要进行数据恢复的情况下显著的降低磁盘&网络带宽的消耗。这个也是CLAY EC插件的最大价值所在。

  • 从Ceph 14版本开始提供，理论上这个特性可以向下backport到低版本。

从clay插件的初始化配置部分的函数实现，也能看到一些与其他插件在兼容适配上的限制

#src/erasure-code/clay/ErasureCodeClay.cc

int ErasureCodeClay::parse(ErasureCodeProfile &profile,
               ostream *ss)
{
  int err = 0;
  err = ErasureCode::parse(profile, ss);
  err |= to_int("k", profile, &k, DEFAULT_K, ss);
  err |= to_int("m", profile, &m, DEFAULT_M, ss);

  err |= sanity_check_k_m(k, m, ss);

  err |= to_int("d", profile, &d, std::to_string(k+m-1), ss);

  // check for scalar_mds in profile input
 //默认采用jerasure插件进行编码
  if (profile.find("scalar_mds") == profile.end() ||
      profile.find("scalar_mds")->second.empty()) { 
    mds.profile["plugin"] = "jerasure"; 
    pft.profile["plugin"] = "jerasure";
  } else {
    std::string p = profile.find("scalar_mds")->second;
   //底层只支持jerasure、isa、shec三种插件
    if ((p == "jerasure") || (p == "isa") || (p == "shec")) {
      mds.profile["plugin"] = p; 
      pft.profile["plugin"] = p;
    } else {
        *ss << "scalar_mds " << mds.profile["plugin"] <<
               "is not currently supported, use one of 'jerasure',"<<
               " 'isa', 'shec'" << std::endl;
        err = -EINVAL;
        return err;
    }
  }



  if (profile.find("technique") == profile.end() ||
      profile.find("technique")->second.empty()) {
    if ((mds.profile["plugin"]=="jerasure") || (mds.profile["plugin"]=="isa") ) {
      mds.profile["technique"] = "reed_sol_van";
      pft.profile["technique"] = "reed_sol_van";
    } else {
      mds.profile["technique"] = "single";
      pft.profile["technique"] = "single";
    }
  } else {
    std::string p = profile.find("technique")->second;
    //Supported techniques are ‘reed_sol_van’, ‘reed_sol_r6_op’,‘cauchy_orig’, ‘cauchy_good’, ‘liber8tion’ for jerasure, 
    if (mds.profile["plugin"] == "jerasure") {
      if ( (p == "reed_sol_van") || (p == "reed_sol_r6_op") || (p == "cauchy_orig")
           || (p == "cauchy_good") || (p == "liber8tion")) {
        mds.profile["technique"] = p;
        pft.profile["technique"] = p;
      } else {
        *ss << "technique " << p << "is not currently supported, use one of "
        << "reed_sol_van', 'reed_sol_r6_op','cauchy_orig',"
        << "'cauchy_good','liber8tion'"<< std::endl;
        err = -EINVAL;
        return err;
      }
      //‘reed_sol_van’, ‘cauchy’ for isa 
    } else if (mds.profile["plugin"] == "isa") {
      if ( (p == "reed_sol_van") || (p == "cauchy")) {
        mds.profile["technique"] = p;
        pft.profile["technique"] = p;
      } else {
        *ss << "technique " << p << "is not currently supported, use one of"
        << "'reed_sol_van','cauchy'"<< std::endl;
        err = -EINVAL;
        return err;
      }
    } else {
    // ‘single’,‘multiple’ for shec.
      if ( (p == "single") || (p == "multiple")) {
        mds.profile["technique"] = p;
        pft.profile["technique"] = p;
      } else {
        *ss << "technique " << p << "is not currently supported, use one of"<<
               "'single','multiple'"<< std::endl;
        err = -EINVAL;
        return err;
      }
    }
  }
  if ((d < k) || (d > k + m - 1)) {
    *ss << "value of d " << d
        << " must be within [ " << k << "," << k+m-1 << "]" << std::endl;
    err = -EINVAL;
    return err;
  }

  q = d - k + 1;
  if ((k + m) % q) {
    nu = q - (k + m) % q;
  } else {
    nu = 0;
  }
//注意分块规则限定k+m+nu总和不能超过254
  if (k+m+nu > 254) {
    err = -EINVAL;
    return err;
  }

  if (mds.profile["plugin"] == "shec") {
    mds.profile["c"] = '2';
    pft.profile["c"] = '2';
  }
  mds.profile["k"] = std::to_string(k+nu);
  mds.profile["m"] = std::to_string(m);
  mds.profile["w"] = '8';

  pft.profile["k"] = '2';
  pft.profile["m"] = '2';
  pft.profile["w"] = '8';

  t = (k + m + nu) / q;
  sub_chunk_no = pow_int(q, t);

  dout(10) << __func__
       << " (q,t,nu)=(" << q << "," << t << "," << nu <<")" << dendl;

  return err;
}

故障恢复时的带宽&磁盘消耗对比

以EC场景下，假设 d = 发生故障时，需要参与数据恢复的OSD数量
在jerasure配置 k=8 m=4的情况下，发生一块磁盘故障，需要读取d=8磁盘才能完成数据的恢复。如果需要恢复的数据的容量为1G，那么需要总共读取 8 x 1 GB = 8GB的数据容量（这也意味着需要同时通过网络传输8GB的数据)。
在clay的插件配置中，d的设置需要满足 k+1 <= d <= k+m-1 的限制，为了满足使d最大化节省磁盘和网络带宽消耗，clay选取d=k+m-1作为默认配置。在k=8，m=4的场景下，根据公式推导可以得到d=8+4-1=11。其中磁盘需要恢复的数据量计算公式如下。其中K为故障时刻需要恢复的数据总量。

插件

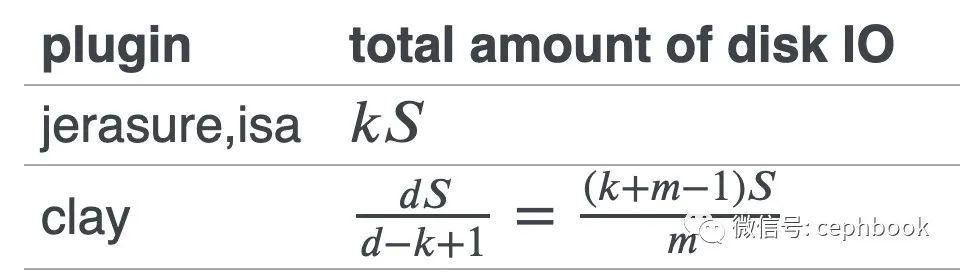
当一个osd故障时，d=11，以需要恢复的数据总量为1GB为例，此时需要恢复下载的磁盘数据总量为

jerasure/isa= 8* 1GB = 8GB
caly = (11*1GB)/(11-8+1) = 11 / 4 = 2.75GB

对比看到caly能够显著的减少磁盘读取数据和网络传输带宽的消耗，caly只用到了isa一类插件的的2.75/8≈34%的资源消耗。

同样的场景下，以k=4，m=2为例，此时d=4+2-1=5，caly只用到了isa一类插件的的2.5/4≈62.5%的资源消耗。

jerasure/isa= 4* 1GB = 4GB
caly = (5*1GB)/(5-4+1) = 5 / 2 = 2.5GB

依次类推，汇总表格如下:

名称 K M D 3副本得盘率 EC得盘率 硬件成本节约比率 磁盘数据迁移量(ISA) 磁盘数据迁移量(CLAY) 数据恢复负载降低比率 4M sub-chunk size(KB) sub-chunk count
2+1 2 1 2 33.33333333 66.66666667 200 2 2 0 2048 1
2+2 2 2 3 33.33333333 50 150 2 1.5 25 512 4
3+1 3 1 3 33.33333333 75 225 3 3 0 1365.333333 1
3+2 3 2 4 33.33333333 60 180 3 2 33.33333333 170.6666667 8
3+3 3 3 5 33.33333333 50 150 3 1.666666667 44.44444444 151.7037037 9
4+1 4 1 4 33.33333333 80 240 4 4 0 1024 1
4+2 4 2 5 33.33333333 66.66666667 200 4 2.5 37.5 128 8
4+3 4 3 6 33.33333333 57.14285714 171.4285714 4 2 50 37.92592593 27
4+4 4 4 7 33.33333333 50 150 4 1.75 56.25 64 16
5+1 5 1 5 33.33333333 83.33333333 250 5 5 0 819.2 1
5+2 5 2 6 33.33333333 71.42857143 214.2857143 5 3 40 51.2 16
5+3 5 3 7 33.33333333 62.5 187.5 5 2.333333333 53.33333333 30.34074074 27
5+4 5 4 8 33.33333333 55.55555556 166.6666667 5 2 60 12.8 64
5+5 5 5 9 33.33333333 50 150 5 1.8 64 32.768 25
6+1 6 1 6 33.33333333 85.71428571 257.1428571 6 6 0 682.6666667 1
6+2 6 2 7 33.33333333 75 225 6 3.5 41.66666667 42.66666667 16
6+3 6 3 8 33.33333333 66.66666667 200 6 2.666666667 55.55555556 25.28395062 27
6+4 6 4 9 33.33333333 60 180 6 2.25 62.5 10.66666667 64
6+5 6 5 10 33.33333333 54.54545455 163.6363636 6 2 66.66666667 5.461333333 125
6+6 6 6 11 33.33333333 50 150 6 1.833333333 69.44444444 18.96296296 36
7+1 7 1 7 33.33333333 87.5 262.5 7 7 0 585.1428571 1
7+2 7 2 8 33.33333333 77.77777778 233.3333333 7 4 42.85714286 18.28571429 32
7+3 7 3 9 33.33333333 70 210 7 3 57.14285714 7.223985891 81
7+4 7 4 10 33.33333333 63.63636364 190.9090909 7 2.5 64.28571429 9.142857143 64
7+5 7 5 11 33.33333333 58.33333333 175 7 2.2 68.57142857 4.681142857 125
7+6 7 6 12 33.33333333 53.84615385 161.5384615 7 2 71.42857143 2.708994709 216
7+7 7 7 13 33.33333333 50 150 7 1.857142857 73.46938776 11.94169096 49
8+1 8 1 8 33.33333333 88.88888889 266.6666667 8 8 0 512 1
8+2 8 2 9 33.33333333 80 240 8 4.5 43.75 16 32
8+3 8 3 10 33.33333333 72.72727273 218.1818182 8 3.333333333 58.33333333 6.320987654 81
8+4 8 4 11 33.33333333 66.66666667 200 8 2.75 65.625 8 64
8+5 8 5 12 33.33333333 61.53846154 184.6153846 8 2.4 70 4.096 125
8+6 8 6 13 33.33333333 57.14285714 171.4285714 8 2.166666667 72.91666667 2.37037037 216
8+7 8 7 14 33.33333333 53.33333333 160 8 2 75 1.49271137 343
8+8 8 8 15 33.33333333 50 150 8 1.875 76.5625 8 64
9+1 9 1 9 33.33333333 90 270 9 9 0 455.1111111 1
9+2 9 2 10 33.33333333 81.81818182 245.4545455 9 5 44.44444444 7.111111111 64
9+3 9 3 11 33.33333333 75 225 9 3.666666667 59.25925926 5.618655693 81
9+4 9 4 12 33.33333333 69.23076923 207.6923077 9 3 66.66666667 1.777777778 256
9+5 9 5 13 33.33333333 64.28571429 192.8571429 9 2.6 71.11111111 3.640888889 125
9+6 9 6 14 33.33333333 60 180 9 2.333333333 74.07407407 2.106995885 216
9+7 9 7 15 33.33333333 56.25 168.75 9 2.142857143 76.19047619 1.326854551 343
9+8 9 8 16 33.33333333 52.94117647 158.8235294 9 2 77.77777778 0.888888889 512
9+9 9 9 17 33.33333333 50 150 9 1.888888889 79.01234568 5.618655693 81
10+1 10 1 10 33.33333333 90.90909091 272.7272727 10 10 0 409.6 1
10+2 10 2 11 33.33333333 83.33333333 250 10 5.5 45 6.4 64
10+3 10 3 12 33.33333333 76.92307692 230.7692308 10 4 60 1.685596708 243
10+4 10 4 13 33.33333333 71.42857143 214.2857143 10 3.25 67.5 1.6 256
10+5 10 5 14 33.33333333 66.66666667 200 10 2.8 72 3.2768 125
10+6 10 6 15 33.33333333 62.5 187.5 10 2.5 75 1.896296296 216
10+7 10 7 16 33.33333333 58.82352941 176.4705882 10 2.285714286 77.14285714 1.194169096 343
10+8 10 8 17 33.33333333 55.55555556 166.6666667 10 2.125 78.75 0.8 512
10+9 10 9 18 33.33333333 52.63157895 157.8947368 10 2 80 0.561865569 729
10+10 10 10 19 33.33333333 50 150 10 1.9 81 4.096 100
11+1 11 1 11 33.33333333 91.66666667 275 11 11 0 372.3636364 1
11+2 11 2 12 33.33333333 84.61538462 253.8461538 11 6 45.45454545 2.909090909 128
11+3 11 3 13 33.33333333 78.57142857 235.7142857 11 4.333333333 60.60606061 1.532360643 243
11+4 11 4 14 33.33333333 73.33333333 220 11 3.5 68.18181818 1.454545455 256
11+5 11 5 15 33.33333333 68.75 206.25 11 3 72.72727273 0.595781818 625
11+6 11 6 16 33.33333333 64.70588235 194.1176471 11 2.666666667 75.75757576 1.723905724 216
11+7 11 7 17 33.33333333 61.11111111 183.3333333 11 2.428571429 77.92207792 1.085608269 343
11+8 11 8 18 33.33333333 57.89473684 173.6842105 11 2.25 79.54545455 0.727272727 512
11+9 11 9 19 33.33333333 55 165 11 2.111111111 80.80808081 0.510786881 729
11+10 11 10 20 33.33333333 52.38095238 157.1428571 11 2 81.81818182 0.372363636 1000
11+11 11 11 21 33.33333333 50 150 11 1.909090909 82.6446281 3.077385424 121
11+12 11 12 22 33.33333333 47.82608696 143.4782609 11 1.833333333 83.33333333 2.585858586 144
12+1 12 1 12 33.33333333 92.30769231 276.9230769 12 12 0 341.3333333 1
12+2 12 2 13 33.33333333 85.71428571 257.1428571 12 6.5 45.83333333 2.666666667 128
12+3 12 3 14 33.33333333 80 240 12 4.666666667 61.11111111 1.404663923 243
12+4 12 4 15 33.33333333 75 225 12 3.75 68.75 1.333333333 256
12+5 12 5 16 33.33333333 70.58823529 211.7647059 12 3.2 73.33333333 0.546133333 625
12+6 12 6 17 33.33333333 66.66666667 200 12 2.833333333 76.38888889 1.580246914 216
12+7 12 7 18 33.33333333 63.15789474 189.4736842 12 2.571428571 78.57142857 0.995140914 343
12+8 12 8 19 33.33333333 60 180 12 2.375 80.20833333 0.666666667 512
12+9 12 9 20 33.33333333 57.14285714 171.4285714 12 2.222222222 81.48148148 0.468221308 729
12+10 12 10 21 33.33333333 54.54545455 163.6363636 12 2.1 82.5 0.341333333 1000
12+11 12 11 22 33.33333333 52.17391304 156.5217391 12 2 83.33333333 0.256448785 1331
12+12 12 12 23 33.33333333 50 150 12 1.916666667 84.02777778 2.37037037 144

 

责任编辑：xj

原文标题：Ceph最新的EC-CLAY插件调研-上

文章出处：【微信公众号：Ceph对象存储方案】欢迎添加关注！文章转载请注明出处。


打开APP阅读更多精彩内容
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。 举报投诉

全部0条评论

快来发表一下你的评论吧 !

下载APP
|投诉反馈|电子发烧友网
© 2021 elecfans.com
湘ICP备2023018690号
×
20
完善资料，
赚取积分