算法大神Tarjan

有同学在学习图论算法的时候，发现这里有个 Tarjan 算法，那里有个 Tarjan 算法，而似乎 Tarjan 算法解决的问题并不一样，于是非常迷惑：Tarjan 算法到底是指什么？

这是一个很好的问题。Tarjan 是计算机领域的大牛，发明了很多现在大家耳熟能详的算法或者数据结构，所以有同学会觉得冠他名字的算法有些多。

但如果我们仔细梳理一下，其实并不复杂。

在这篇文章中，我会带领大家梳理一下 Tarjan 发明的算法都有哪些，整体脉络是怎样的。

注意：在这篇文章中，我不会具体讲解某个算法的原理。但是，我会给出很多具体的关键字，并且标红。如果大家对某个算法想深入了解，可以以此为引，在互联网上搜索学习。

我相信，互联网上关于某个具体算法的资料是非常多的，反而是这样按照某个脉络做总结的文章很少。

首先，Tarjan 是一名美国的计算机科学家和数学家，全名 Robert Endre Tarjan。

先来一个 Tarjan 大神的名言镇楼：

一般提起 Tarjan 算法，通常是指 Tarjan 发明的求解有向图的强联通分量算法，全称是 Tarjan’s Strongly Connected Components Algorithm. 

为什么这么叫？因为求解有向图的强联通分量还有一个著名算法：Kosaraju 算法。Kosaraju 算法也是以他的发明者的名字命名的。

我在算法比赛中，或者需要求解 SCC（强连通分量的缩写：Strongly Connected Components） 问题的时候，喜欢写 Kosaraju 算法。因为 Kosaraju 算法的实现非常简单，复杂度和 Tarjan 算法是一样的，都是 O(V + E) 的。

但实际上，Kosaraju 算法需要遍历两次图，而 Tarjan 算法只需要遍历一次图。所以，Tarjan 算法的性能更高，一般可以高 30% - 40% 左右。

而 Tarjan 算法之所以有名，关键在于使用 Tarjan 算法的思想，不仅仅可以求解 SCC 问题，还可以求无向图中的桥或者割点。

这就是为什么，很多同学看到 Tarjan 算法，做的事情不一样，但都叫 Tarjan 算法的原因。我们可以把 Tarjan 算法理解成是一种思想，基于这种思想，可以求解桥，割点，和 SCC 问题。

所谓的 Tarjan 算法思想，就是在遍历整个图的过程中，对每一个遍历的节点记录一个时间戳，通常被称为是 DFN；同时，记录通过这个节点，不经过父亲节点，最早能回到的时间戳，通常被称为是 LOW。通过这些信息，就能判断一个图的桥，割点，和强连通分量。

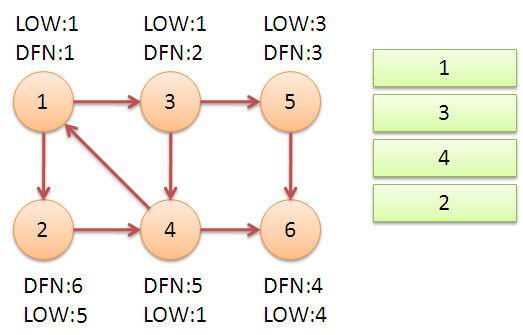
然而，Tarjan 的贡献远不止于此。以Tarjan命名的另外一个非常著名的算法，叫 Tarjan‘s Off-line Least Common Ancestors Algorithm。

这个算法本质是借助并查集，求解 LCA（最近公共祖先的缩写：Least Common Ancestors）问题。

实际上，离线的 LCA 问题，是计算机科学领域非常著名的问题，深究下去，和 Binary Lifting，RMQ 等非常著名的算法思想都有联系。

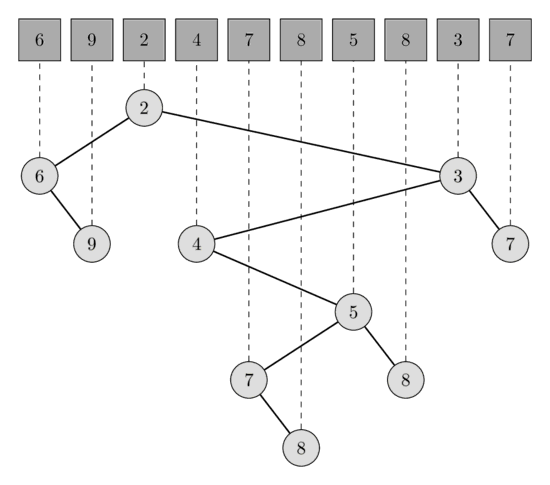
说到并查集，Tarjan 也和这种数据结构有不解之缘。并查集虽然不是 Tarjan 发明的，但是并查集的复杂度是 Tarjan 首先分析清楚的：也就是 Ackerman 函数的反函数。

如果对此感兴趣的同学，可以翻看《算法导论》，《算法导论》对这部分内容介绍得很清楚。

实际上，这也是《算法导论》这本教材的意义：稍微深入一些的算法分析问题，一般的算法教材都不会涉及。而《算法导论》所覆盖的深度和广度，比大多数教材都高太多。

当然，这也是《算法导论》不适合入门的原因。

 

说到数据结构，Tarjan 确实发明过数据结构。最有名的两个，一个是斐波那契堆，一个是 Splay 树。

Splay 树虽然不保证一定平衡，但各个操作的均摊复杂度是 O(logn) 级别的。

Splay 树最大的优势是实现简单，比红黑树简单不知道多少倍。所以，如果我们需要调用更加底层的树操作，需要自己实现一个自平衡的二分搜索树时，通常 Splay 树是首选。

也正因为如此，很多搞竞赛的同学，都是能手写 Splay 树的。

Tarjan 还是非常著名的算法：BFPRT 的作者之一。其实 BFPRT 这个算法的名字，是其五个作者首字母的缩写。其中的 T，就是 Tarjan。

BFPRT 这个名字听起来非常拗口，同时也难记，但是它的另一个名字就很简单直接了，就是 Median of Medians。

这个算法整体并不难理解，是快排思想的一种更稳定的优化，每次近乎可以保证选取所处理的数组的中位数作为标定点（pivot），使得快速排序的最差时间复杂度真真正正达到了 O(nlogn)。

值得一提的是，BFPRT 算法的这五位作者，都是计算机科学领域的大牛。他们分别是：

B 是 Blum，全名 Manuel Blum，他因为复杂度理论方面的贡献，以及密码学的应用，获得了 1995 年的图灵奖；

F 是 Floyd，全名 Robert W. Floyd，相信大家都很熟悉。大家在算法课本上一定会学到的所有点对的最短路径算法，就是他和 Warshall 一起提出的，即 Floyd–Warshall 算法。同时，Floyed 还提出了非常著名的 Floyed 环检测算法。他获得了 1978 年的图灵奖；

P 是 Pratt，全名 Vaughan Pratt，是斯坦福的教授；

R 是 Rivest，全名 Ron Rivest。他是 MIT 的教授，专攻密码学。我们现在所经常使用的 MD5 算法，他就是作者之一；

最后的 T，就是这篇文章的主角：Tarjan，全名 Robert Endre Tarjan。

在图论领域，Tarjan 还改进了一个非常著名的算法：最小树形图。最小树形图这个名字听起来很复杂，但其实这个概念很简单：就是有向图的最小生成树。

解决最小树形图问题，有一个非常朴素的算法，叫朱刘算法。听这个名字大家也知道，这是两位华人科学家首先提出来的算法，在论文记载中，分别是  Y.J. Chu 和 T.H. Liu 在 1965 年提出来的。朱刘算法的时间复杂度是 O(VE) 的。

后来，Tarjan 改进了这个算法，可以使用 O(ElogV) 的时间做预处理，之后使用 O(V) 的时间，求解图中以任意顶点为根的最小树形图

Tarjan 还发明了一种平面图的检测算法，首次在线性时间解决了平面图检测问题（Planarity-Testing）。因为平面图检测离大多数同学的工作比较远，所以可能很少有同学了解这个算法。

Tarjan 的平面图检测算法还有一个合作者：John Hopcroft。他们二人因为这个算法，以及在算法和数据结构等基础领域对计算机科学的贡献，获得了 1986 年的图灵奖。

Tarjan 的硕士和博士是在斯坦福大学读的。他的导师有两个。一个就是大名鼎鼎的 Floyd，上文介绍 BFPRT 算法的时候介绍了。在这里给一个年轻的时候，Floyd 风流倜傥的帅照：

 

Tarjan 的另一名导师，则是计算机科学领域的神级人物：Donald Knuth。他可以说是计算复杂领域的创始人。

Donald Knuth 的经历和贡献，可以写一本书了。有时间，我会再写一篇文章介绍他。现在，很多人了解他，都是因为他的神作：TAOCP，即 The Art of Computer Programming，被中文翻译成《计算机程序设计艺术》。这套书被评为至今计算机科学史上最重要的神作，但其实还没有写完。

 

不过 Donald Knuth 对计算机科学领域的贡献，远不止一套书这么简单。要聊 Donald Knuth 的话，能聊的就太多。这篇文章我们收一收，说回 Tarjan。

Tarjan 现在还在世，今年已经 72 岁了。根据维基百科，现在 Tarjan 在普林斯顿任教。

实际上，在计算机科学领域，很多在教科书中出现的人物，都还在世；很多教科书级别的算法，概念，理论，其实距离提出，也不过是几十年的时间。

这足以可见：计算机是多么年轻的一个学科。

也正是因为这个原因，在计算机科学领域中，还有大量的没有被完全解决的问题。

计算机科学领域其实还大有可为。

责任编辑：xj

原文标题：Tarjan 这个算法大神

文章出处：【微信公众号：算法与数据结构】欢迎添加关注！文章转载请注明出处。