

SDMA扩频原理
通信设计应用
65人已加入
描述
SDMA扩频原理
小波分析的基础理论为寻找合适的正交小波函数族提供了强有力的理论依据,也是SDMA的数学基础.小波函数定义为
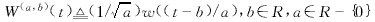 (1)
(1)
式中w(t)称为基本小波.实际应用中,通常采用进二小波,定义为
ψmn(t)2m/2ψ(2mt-n) (2)
根据小波函数性质,有<ψmn.ψkl>=δm,kδn,l,其中δi,j=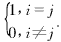 对任意信号x(t),其离散二进小波变换及反变换为
对任意信号x(t),其离散二进小波变换及反变换为
xmn=∫+∞-∞x(t)ψmn(t)dt (3a)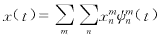 (3b)
(3b)
现在考虑M条二进制码流sm∈{0,1},m=1,2,…,M,对于在L2(R)上的正交集ψmnT,可将sm合并为
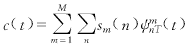 (4)
(4)
其中n表示一个序列的第n个比特,T是一个比特的持续时间.因此,在接收端信号的解调就是根据(3b)对c(t)进行小波变换以提取序列sm.下面从式(4)出发来推导c(t)的功率谱表达式.
c(t)的自相关函数为
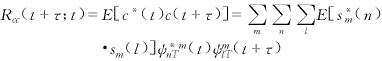
假定信息序列{sm(n)},m=1,2,…,M,是广义平稳过程,其自相关函数定义为Rss(k)=E[s*m(n).sm(n+k)],所以
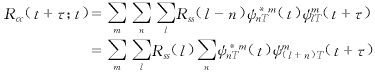
因为c(t)为广义周期平稳过程,故有
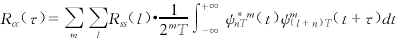 (5)
(5)
从式(5)的傅立叶变换得到c(t)的功率谱密度表达式
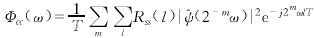 (6)
(6)
其中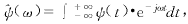 ,并定义信息序列的谱密度为
,并定义信息序列的谱密度为
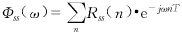
代入式(6)就得到Φcc(ω)的进一步表达式
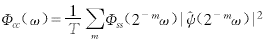 (7)
(7)
从式(7)可以看出,信息序列经过小波变换编码后,其频谱得到了扩展,并且扩频系数η=2m,m>0.可见,各信道的扩频系数是不相同的.
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
- 相关推荐
- 热点推荐
- SDMA
-
求助,SDMA M2M脚本很慢,是不是使用了BURST DMA Unit?2023-06-01 1094
-
如何在iMX6上与EIM一起使用SDMA?2023-04-11 542
-
是否必须更改任何其他定义才能使用SDMA3而不是SDMA1?2023-03-28 467
-
如何运用MATLAB及EPROM简化扩频电路设计?2021-04-23 1236
-
扩频理论的基础和益处?2020-12-18 1501
-
OFDM系统的扩频性能分析2012-02-13 1138
-
扩频技术详解2011-11-07 10449
-
空分多址(SDMA),空分多址(SDMA)是什么意思2010-04-03 3957
-
基于有限反馈的数据流数自适应SDMA2009-11-21 826
-
基于SDMA的调制解调模型2009-10-21 1038
-
扩频通信技术教程2009-05-22 11277
-
什么是扩频通信,扩频通信的定义2009-05-20 6990
-
自编码扩频和直接序列扩频的性能比较2009-02-18 605
全部0条评论

快来发表一下你的评论吧 !

