

波导端头裂缝有限相控阵单元的阵中特性
嵌入式设计应用
描述
波导端头裂缝有限相控阵单元的阵中特性
本文利用矩量法对以矩形波导端头裂缝为辐射单元的有限相控阵的单元阵中方向图及口面磁流分布进行了计算.讨论了不同位置辐射单元在不同扫描角时互耦对口面分布的影响.
关键词:相控阵;单元阵中方向图;磁流
Unit Characteristic of Rectangular Waveguide End-Solt Finite Phased Arrays
LI Jian-ying,LIANG Chang-hong
(Xidian University,National Laboratory of Antenna and Microwave Technology,Xi'an 710071,China)
Abstract:Element patterns and equivalent magnetic currents of rectangular waveguide end-slot finite phased arrays are analysed using moment method.Effect of mutual coupling for elements in different position at different scan angle to equivalent magnetic current distribution is discussed.
Key words:phased arrays;element pattern in arrays;magnetic currents
一、引 言
随着通讯及雷达技术的发展,单元数较少的相控阵及非扫描阵列的使用越来越多.由于单元间互耦的影响再加上阵列单元数较少等原因,增加了分析和设计的难度.对于波导端头裂缝有限相控阵而言,研究人员关心的问题是边沿单元与中心单元扫描特性所存在的不同及单元的阵中方向图等辐射单元的阵中特性,这些问题最终可归结为对相控阵单元的口面等效磁流分布的分析,分析阵中辐射单元的口面等效磁流分布是研究该类有限相控阵性能的基础.
利用矩量法对波导端头裂缝有限阵列进行分析,对于较小的相控阵(几百个单元)可以得到准确的计算结果.本文主要对波导端头裂缝有限相阵的辐射单元在阵中的口面分布及阵中单元方向图等特性进行了分析计算.
二、理论分析
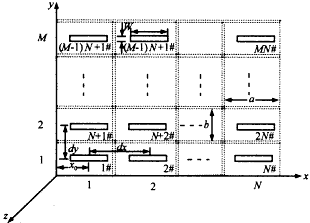
矩形波导馈电裂缝组成的相控阵的结构及坐标系如图1所示,单元以矩形栅格排列,单元的横向间距为dx,纵向间距为dy,共M行N列.波导的内尺寸宽边为a窄边为b,缝位于矩阵波导端头的同一无穷大金属良导体平面上,导体的厚度为t,缝隙长为L,宽为W.有限阵列中所有缝的几何尺寸相同.
|
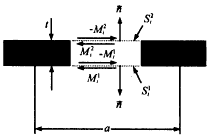
图1 有限阵的结构 假定缝隙很窄(L/W>10),波导壁为理想良导体,波导内仅传输由z负无穷方向激励的TE10波.如图2所示把缝隙天线结构分成波导内部区域a、腔体b、和半空间c几个区域,M1i,M2i(i=1,2,…,M×N)分别为缝隙口面S1i,S2i(i=1,2,…,M×N)上的磁流分布,在S1i,S2i(i=1,2,…,M×N)上磁场的切向分量必须连续.在S1i(i=1,2,…,M×N)面上,磁场的切向分量的产生有三个源,其一是波导内部的激励
|
|
图2 缝分区及等效磁流
方程式(1a)中,
Gxxa为波导内部并矢格林函数的xx分量;
akis(k=1,2)为第i个波导上裂缝的Ski面上磁流Mki的展开系数.
取权函数:
x0为缝位于所在波导上的位置(如图1所示). (Yiaals+YAls)a1is+Yiablsa2is=Hini (5a) 式(5b)中j2=2×j,Na为基的个数,取Nb=M×N为相阵单元总的个数,把i遍取1,2,…,M×N,则方程(5)可构成一个Ne阶矩阵方程(Ne=2×M×N×Na): [Aij].AT=HT (6) 其中AT与HT为A及H的转置矩阵, A=(a11s,a21s,a12s,a22s,…,a1Nbs,a2Nbs) (7) a11s,a21s,a12s,a22s,…,a1Nbs,a2Nbs为待求的未知量,a1is,a2is,(i=1,2,…,Nb)都为Na列的子列矩阵,即(s=1,…,Na).
其中,i为单元的编号,在计算a2is时由于高阶模的幅度还不到主模的幅度的3%,所以为简单起见,仅取主模进行计算,不影响计算结果的精度. H=(p1×Hin1s,0,p2×Hin2s,0,…,pNb×HinNbs,0) (10) 此时激励幅度(p1,p2,…,pNb)可以为复数,即包括相位信息,利用式(10)可计算非等幅激励或在某一扫描角时阵列的口面分布A. 三、计算实例 |
|
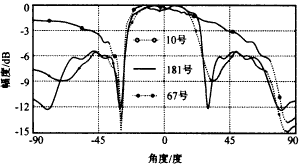
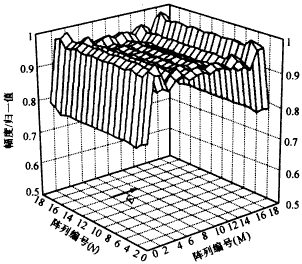
图3 单元阵中方向图(E面) 假设天线阵列为等幅激励,通过计算所得的阵列中心单元及边沿单元的口面分布如图4所示,(a)为扫描角为0°时单元的口面分布,(b)为E面扫描角为25°时单元的口面分布,从这里可以看到扫描角的变化对互耦的影响. |
|
(a) 扫描角为0° |
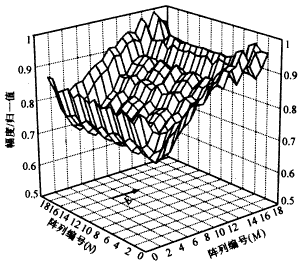
|
(b) E面扫描角为25° 四、总 结 |
-
相控阵雷达电源芯片详解2024-11-17 9158
-
微环谐振腔集成波导光延时线研究2010-04-24 2083
-
室内双色点阵单元2013-07-15 2110
-
浅析阵列天线和相控阵2019-06-12 4586
-
柱面共形裂缝阵天线设计2019-07-03 1578
-
一种新型的单层宽带反射阵单元天线设计2019-07-17 1808
-
STM32F103如何驱动32x64双色点阵单元板?2022-02-09 1129
-
了解毫米波相控阵 -- 之二2023-05-06 709
-
卫星系统中折叠波导的展开形变及电特性研究2010-01-13 1023
-
光子晶体波导传输特性研究2010-09-23 732
-
高功率半导体激光器标准列阵单元及散热器的设计与制作2010-11-23 582
-
基于光学相控阵理论的阵列集成光波导的分析2017-10-30 1533
-
阵面安装误差对相控阵雷达测角精度的影响2018-02-27 1137
-
一文详解光波导相控阵技术2023-04-23 3794
-
相控阵天线为什么做成面阵 频控阵与相控阵的区别2023-07-11 2616
全部0条评论

快来发表一下你的评论吧 !

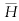 inti,其二是M1i,其三是M2i,在S2i(i=1,2,…,M×N)面上,磁场的切向分量的产生有M×N+1个源,其一是M1i,其它是M2j(j=1,2,…,M×N),由磁场的切向分量的连续性,对于每一个i(i=1,2,…,M×N)可得如下方程组:
inti,其二是M1i,其三是M2i,在S2i(i=1,2,…,M×N)面上,磁场的切向分量的产生有M×N+1个源,其一是M1i,其它是M2j(j=1,2,…,M×N),由磁场的切向分量的连续性,对于每一个i(i=1,2,…,M×N)可得如下方程组: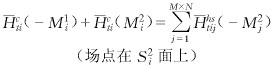 (1b)
(1b)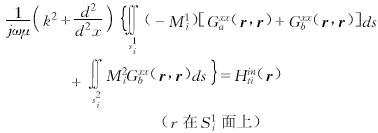 (2a)
(2a)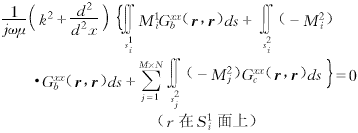 (2b)
(2b)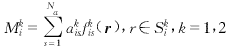 (3)
(3)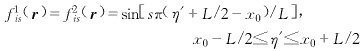
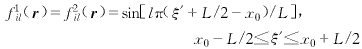
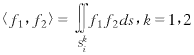 (4)
(4)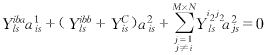 (5b)
(5b)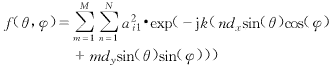 (9)
(9)