

几乎周期时变MA系统的辨识
嵌入式设计应用
描述
几乎周期时变MA系统的辨识
本文利用循环统计量讨论几乎周期时变滑动平均(APTV-MA)系统的辨识问题.提出了基于奇数阶时变累量的参数估计的法方程方法,并导出了基于时变累量和循环累量的系统模型定阶方法.仿真实验说明了本文所提方法的性能.
关键词:循环统计量;几乎周期时变MA系统;法方程;系统辨识
Identification of Almost Periodic Time-Varying MA Systems
LI Hong-wei
(Department of Mathermatics and Physics,China University of Geoscience,Wuhan 430074,China)
YUAN Bao-zong
(Institute of Information Science,Northern Jiaotong University,Beijng 100044,China)
Abstract:This paper addresses the problem of identification of almost periodic time-varying moving average (APTV-MA) systems using cyclic statistics.The normal equation approaches based on odd order time-varying cumulants are presented for parameters estimation.Model order detemination procedures based on time-varying and cyclic cumulants are also derived.Simulations are performed to illustrate performance of the presented methods.
Key words:cyclic statistics;almost periodic time-varying MA system;normal equation;identification of system
一、引 言
考虑q阶几乎周期时变滑动平均(APTV-MA)信号模型
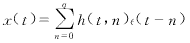 (1)
(1)
并且,假设下列假定成立.
假定1 激励噪声?(t)是零均值独立同分布的,且存在一个奇数k(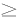 3),使得其k阶累量γk?满足0<|γk∈|<+∞.
3),使得其k阶累量γk?满足0<|γk∈|<+∞.
假定2 对于每一个固定的n,有限冲激响应序列h(t,n)是关于t的几乎周期实序列(可以是非最小相位的),并且,h(0,0)=1;h(t,0)≠0,h(t,q)≠0,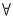 t.
t.
在实际应用中,信号x(t)是在噪声中被观测的:
y(t)=x(t)+v(t),t=0,1,…,T-1 (2)
其中,加性噪声v(t)满足
假定3 v(t)是一个与∈(t)独立的功率谱未知的零均值高斯(有色)过程(可以是非平稳的).
在模型(2)下,y(t)是非平稳的,原有的讨论时不变MA系统的辨识方法不能直接应用.易证y(t)是循环平稳的.因此,我们的目的是根据观测值{y(t),t=0,1,…,T-1}利用循环统计量来估计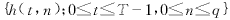
上述问题可以看作时不变MA系统在几乎周期时变情形的推广.这一类问题在通讯,水文气象等领域具有广泛的应用[5,11,14].在高斯信号情形,文献[15]提出了基于二阶统计量的近似最大似然技术估计信号参数.相关问题的讨论可见文献[8]和[13].最近[5],Dandawate和Giannakis对于几乎周期时变MA信号进行了较深入的研究,他们利用高阶循环统计量来辨识APTV-MA系统,提出了模型参数估计的线性和非线性算法以及一种统计的定阶方法.
众所周知,对于时不变MA系统,基于高阶累量的参数估计方法可分为闭式解,法方程和非线性最优化解三大类[12].由于不涉及极值问题求解,前二种线性方法尤其令人重视[7,17].但是到目前为止,对于几乎周期时变MA系统的辨识,这两种方法的研究还较小.本文讨论利用循环统计量辨识APTV-MA系统的新方法,提出了参数估计的法方程方法和基于时变累量和循环累量的时域定阶方法.
二、参数估计方法
在本节先假定几乎周期时变MA系统的阶q已知,推导APTV-MA信号参数的法方程.
实信号z(t)的k阶时变的和循环的累量分别定义[3,5]为
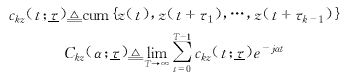
其中,τ=(τ1,…,τk-1).有关循环统计量的详细定义和记号参见文献[3].
当k 3时,由假定3和累量性质有ckx(t;τ)=cky(t;τ).即观测信号y(t)与无加性噪声污染的输出信号x(t)具有相同的时变累量,因此,在基于高阶时变和循环累量的分析中不必考虑加性高斯噪声的影响.
3时,由假定3和累量性质有ckx(t;τ)=cky(t;τ).即观测信号y(t)与无加性噪声污染的输出信号x(t)具有相同的时变累量,因此,在基于高阶时变和循环累量的分析中不必考虑加性高斯噪声的影响.
由累量性质可知,满足模型(1)和假定1~2的APTV-MA信号x(t)的k(>3)阶时变累量为
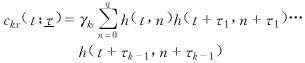 (3)
(3)
它是时不变MA系统的BBR公式[1]在APTV-MA情形的推广.
令τ1=τ2=…=τk-2=q,则由式(3)得到
ckx(t;q,…,q,τk-1)=γk∈h(t,0)hk-2(t+q,q).h(t+τk-1,τk-1) (4)
利用上式不难得到
ckx(t-i;q,…,q,i)=γk∈h(t-i,0)hk-2(t-i+q,q)h(t,i)
ckx(t-i;q,…,q,q)=γk∈h(t-i,0)hk-1(t-i+q,q)
ckx(t-i;q,…,q,0)=γk∈h2(t-i,0)hk-2(t-i+q,q)
由上述得到
γk∈hk(t;i)=ckkx(t-i;q,…,q,i)/[ck-2kx(t-i;q,…,q,q).ckx(t-i;q,…,q,0)] (5)
由上式(t=i=0)和假定2(h(0,0)=1)可知,
γk∈=ck-1kx(0;q,…,q,0)/ck-2kx(0;q,…,q,q) (6)
当k为奇数时,
h(t,i)=ckx(t-i;q,…,q,i)/{γ1/kkx[ck-2kx(t-i;q,…,q,q)
.ckx(t-i;q,…,q,0)]1/k} (7)
因此,当k为奇数时,由式(6)和式(7)可以获得冲激响应序列h(t,i).当k为偶数时,由式(6)和式(7)只能得到h(t,i)的幅值,而无法判定其符号.相应于时不变情形的结果见文献[6].
特别地,当k=3时,式(6)和式(7)成为
γ3∈=c33x(0;q,0)/c3x(0;q,q)
h(t,i)=c3x(t-i;q,i)/{γ1/33∈[c3x(t-i;q,q)
.c3x(t-i;q,0)]1/3}
文献[5]也得到了上式,式(6)和式(7)将文献[5]的结果推广到任意奇数阶累量情形.
虽然在奇数阶情形可以利用式(6)和式(7)来估计h(t,i),但是与时不变情形类似,这种方法将产生较大的估计误差,考虑下面的法方程方法.
在式(3)中,令τ1=i,τ2=…=τk-1=0,得到
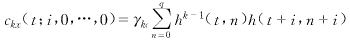 (8)
(8)
式(8)可以变换为
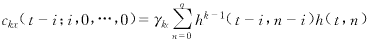 (9)
(9)
记
B1 (ckx(t+q;-q,0,…,0),ckx(t+q-1;
(ckx(t+q;-q,0,…,0),ckx(t+q-1;
-q+1,0,…,0),…,ckx(t-q;q,0,…,0))T.
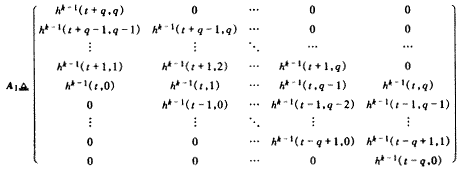
H1 (γk∈h(t,0),γk∈h(t,1),…,γk∈h(t,q-1),γk∈h(t,q))T.
(γk∈h(t,0),γk∈h(t,1),…,γk∈h(t,q-1),γk∈h(t,q))T.
在式(9)中令i=-q,-q+1,…,-1,0,1,…,q,可得
A1H1=B1 (10)
将式(6)和式(7)代入A1,求解超定线性方程组(10),可以得到γk∈和h(t,n).
方程(10)是本文得到的基于时变累量的APTV-MA系统参数的线性法方程.在A1中,考虑其前q+1行构成的三角阵,由假定2可知这个三角阵的对角线元素用式(6)和式(7)中的时变累量代入均不为零,三角阵是满秩的,故秩A1=q+1.因此,易得如下的唯一识别定理.
定理1 在模型(1)之下,假定信号的k阶累量已知,则由方程(10)确定的H1的解是唯一的.
在实际的估计计算中,为求解线性方程组(10),需要将A1和B1中的元素用其估计值代替,有关循环统计量的估计将在第四节中讨论.
由式(8)得到另一类法方程,记
A2
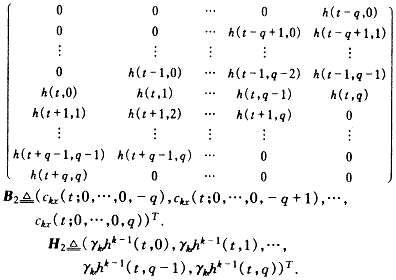
在式(8)中令i=-q,-q+1,…,-1,0,1,…,q,可得
A2H2=B2 (11)
将式(6)和式(7)代入A2,求解超定线性方程组(11),得到γk∈和h(t,n)的幅值,其符号可由式(6)和式(7)确定.
方程(11)是得到的基于时变累量的另一类线性法方程,类似于式(10)的讨论可知,秩A2=q+1.因此,可得如下的唯一识别定理.
定理2 在模型(1)之下,假定信号的k阶累量已知,则由方程(11)确定的H2的解是唯一的.
三、APTV-MA模型定价
在上节的讨论中,假定APTV-MA系统的阶q是已知的,在许多实际问题中,模型的阶是未知的.因此,本节计论APTV-MA系统阶次的确定问题.
根据式(8),有
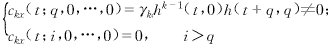 (12)
(12)
以上两式指出,APTV-MA的阶数q是使ckx(t;i,0,…,0)≠0满足的最大正整数imax.因此,定阶问题转化为判定时变累量是否为零的问题.与时不变MA情形一样,在估计计算中,对于一组在噪声中观测到的有限长度数据,由样本估计检验累量为零成立与否的阈值是难以确定的.为了解决这个问题,文献[16]在讨论时不变MA系统定价问题时,提出了一种新颖的时域定阶方法,该方法易于实现,且具有较好的数值鲁棒性.受该方法的启发,讨论APTV-MA信号的定阶.
1.基于时变累量的模型定阶
利用信号x(t)的k阶时变累量构造矩阵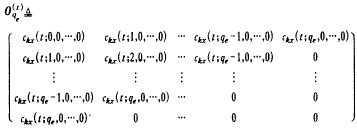 (13)
(13)
其中,qe(>q)是模型阶次的上界(它在实际应用中是容易取到的),由式(12)可知,秩O(t)qe=q+1.因此,模型的阶确定转化为矩阵(13)的秩的确定.
在实际应用中,式(13)中的元素用样本估计代替,用奇异值分解[2]求O(t)qe的有效秩,即可确定APTV-MA的阶数.
由式(13),矩阵O(t)qe的有效秩的确定实际上等价于验证
ci+1kx(t;i,0,…,0)≠0,i>0
使得上式成立的最大正整数imax即是模型的阶数q.因此,基于时变累量的APTV-MA的定阶方法如下,将ckx(t;i,0,…,0)用其样本估计 kx(t;i,0,…,0)代替,选择使得
kx(t;i,0,…,0)代替,选择使得
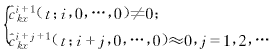 (14)
(14)
成立的最大正整数imax作为阶数q的估计.
2.基于循环累量的模型定价
上一小节讨论的是基于t时刻时变累量的定阶方法,下面讨论基于循环累量的定阶方法,由时变累量和循环累量的关系[3],有
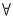 t,ckx(t;τ)=0
t,ckx(t;τ)=0
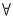 α,Ckx(α;τ)=0
α,Ckx(α;τ)=0
由式(12),有
至少存在一个α0,使得Ckx(α0;q,0,…,q)≠0;
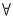 α,Ckx(α;i,0,…,0)=0,i>q (15)
α,Ckx(α;i,0,…,0)=0,i>q (15)
模型定阶转化为找使上两式成立的最大正整数imax.根据上节的讨论,对于某一α0的qe>q,构造矩阵O(c)qe(见式(16)).易知秩O(c)qe=q+1,即模型定阶转化为判定矩阵O(c)qe的秩.
在实际应用中,尽管可以用奇异值分解来判定O(c)qe的有效秩,但必须先找α0,这在应用中是相当麻烦的.然而,类似上一小节的讨论,对于某一α0,只须找到使Ci+1kx(α0;i,0,…,0)≠0成立的最大的正整数imax作为模型阶数q的估计.这等价于选择使得[supα|Ckx(α;i,0,…,0)|]i+1≠0成立的最大的正整数imax作为模型阶数q的估计.
O(c)qe
 (16)
(16)
因此,基于循环累量的APTV-MA的定阶方法如下,将Ckx(α;i,0,…,0)用其样本估计代替,选择使得
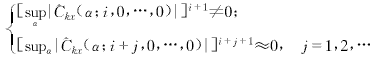 (17)
(17)
成立的最大正整数imax作为阶数q的估计.
四、样本估计和收敛性讨论
在上两节中,提出了APTV-MA系统的定阶方法和参数估计的法方程方法,它们是基于时变的和循环的累量进行的.在实际的估计计算中,这些统计量只能由有限长度的样本(观测数据) 进行估计而得到.
进行估计而得到.
对于满足模型(2)和假定1-3的APTV-MA信号y(t),由循环累量的定义可知,当k 3时,Cky(α;τ)=Ckx(α;τ).若要估计ckx(t;τ)和Ckx(α;τ),只须估计cky(t;τ)和Cky(α;τ).
3时,Cky(α;τ)=Ckx(α;τ).若要估计ckx(t;τ)和Ckx(α;τ),只须估计cky(t;τ)和Cky(α;τ).
对于一般的k阶情形,cky(t;τ)和Cky(α;τ)的强相容估计可以按照文献[9]的方法得到.
对于k=1,有c1y(t)=C1y(α)=0.
对于k=3,y(t)的三阶循环矩和时变矩估计分别为
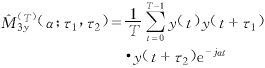 (18)
(18)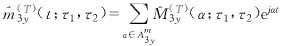 (19)
(19)
其中,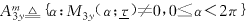 ,y(t)的三阶时变累量和循环累量估计分别为
,y(t)的三阶时变累量和循环累量估计分别为
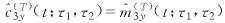 (20)
(20)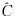 (T)3y(α;τ1,τ2)=
(T)3y(α;τ1,τ2)=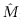 (T)3y(α;τ1,τ2) (21)
(T)3y(α;τ1,τ2) (21)
在上述估计中,循环矩估计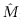 (T)3y(α;τ)是一个关键的估计量,时变的和循环的累量估计都是由它获得的.另外有一个量需要估计的是Am3y.关于它的估计,有两种方法.一种是统计检验方法[4],另一种是基于DFT的直接检验方法[10].
(T)3y(α;τ)是一个关键的估计量,时变的和循环的累量估计都是由它获得的.另外有一个量需要估计的是Am3y.关于它的估计,有两种方法.一种是统计检验方法[4],另一种是基于DFT的直接检验方法[10].
在模型(2)的假定之下,由文献[9]的定理,可知上述关于时变累量和循环累量的估计都是其真值的强相容估计.由前两节的参数唯一识别定理和矩阵扰动分析理论可知,上两节提出的参数和阶数估计均是强收敛的.
五、仿真实验
为了检验本文提出的基于时变和循环累量的模型定阶方法和参数估计的法方程方法对APTV-MA信号的定阶和参数估计的性能,进行了如下的仿真实验.
例 驱动噪声?(t)是零均值独立的指数分布随机数,并且,σ2?=1,γ3∈=2.加性噪声v(t)取为零均值AR(2)高斯过程:
v(t)-1.6v(t-1)+0.68v(t-2)=e(t) (22)
APTV冲激响应序列h(t,n)取为关于t的周期为2的实序列:
t为偶数时:h(t,0)=1,h(t,1)=0.2,t(t,2)=-0.75
t为奇数时:h(t,0)=0.6,h(t,1)=-0.65,t(t,2)=1.2
即无噪声污染的信号x(t)是一个周期为2的时变MA(2)过程.当t为偶数时,x(t)=∈(t)+0.2∈(t-1)-0.75∈(t-2).它是最小相位的,其零点为0.7713和-0.9713.当t为奇数时,x(t)=0.6∈(t)-0.65∈(t-1)+1.2∈(t-2).它是非最小相位的,其零点为0.5417±1.3064j.信噪比定义为SNR=10log10(σ2?/σ2v).
在实验中,信噪比取为0dB,观测数据由上述参数和式(2)产生.数据长度取为8192,Monte Carlo运行次数为100.基于三阶时变累量和法方程方法(式(10))的参数估计的统计结果见表1.基于t=0时刻的三阶时变累量的定阶统计结果见表2.基于三阶循环累量的定阶统计结果见表3.
表1 基于三阶时变累量的参数估计的统计结果
| 待估参数 | γ3? | h(0,1) | h(0,2) | h(1,0) | h(1,1) | h(1,2) |
| 真值 | 2.00000 | 0.20000 | -0.75000 | 0.60000 | -0.65000 | 1.20000 |
| 估计均值 | 2.02758 | 0.26036 | -0.75511 | 0.61655 | -0.59606 | 1.16906 |
| 标准偏差 | 0.29703 | 0.09312 | 0.11403 | 0.12365 | 0.12205 | 0.18681 |
|
表2 基于三阶时变累量的定阶统计结果 |
| i值 | 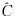 3y(0;i,0) 3y(0;i,0) |
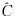 i+13y(0;i,0) i+13y(0;i,0) | ||
| 均值 | 标准偏差 | 均值 | 标准偏差 | |
| i=1 | -0.45716 | 0.17114 | 0.23829 | 0.16242 |
| i=2* | 0.88060 | 0.28343 | 0.90109 | 0.83031 |
| i=3 | -0.01843 | 0.14205 | 0.00112 | 0.00243 |
| i=4 | 0.02757 | 0.20303 | 0.00085 | 0.00387 |
| i=5 | 0.04614 | 0.15643 | 0.00050 | 0.00270 |
| i=6 | 0.00925 | 0.18165 | 0.00006 | 0.00055 |
| i=7 | 0.01157 | 0.12909 | 0.00001 | 0.00003 |
| i=8 | 0.01862 | 0.21002 | 0.00004 | 0.00084 |
| i=9 | 0.01646 | 0.14416 | 0.00000 | 0.00002 |
| i=10 | 0.01380 | 0.17514 | 0.00000 | 0.00002 |
|
表3 基于三阶循环累量的定阶统计结果 |
| i值 | supα|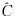 3y(α;i,0)| 3y(α;i,0)| |
supα|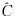 i+13y(α;i,0)| i+13y(α;i,0)| | ||
| 均值 | 标准偏差 | 均值 | 标准偏差 | |
| i=1 | 0.74568 | 0.11763 | 0.56988 | 0.18373 |
| i=2* | 1.17688 | 0.16014 | 1.72152 | 0.70514 |
| i=3 | 0.47164 | 0.05893 | 0.05441 | 0.03061 |
| i=4 | 0.44282 | 0.05312 | 0.01968 | 0.01309 |
| i=5 | 0.40810 | 0.04865 | 0.00577 | 0.00514 |
| i=6 | 0.39960 | 0.04397 | 0.00211 | 0.00184 |
| i=7 | 0.37370 | 0.04522 | 0.00058 | 0.00074 |
| i=8 | 0.38182 | 0.04109 | 0.00026 | 0.00031 |
| i=9 | 0.36517 | 0.03844 | 0.00007 | 0.00009 |
| i=10 | 0.38063 | 0.04190 | 0.00005 | 0.00009 |
| 表1说明参数估计的法方程方法具有较好的估计匀值和较小的标准偏差.特别要指出的是,例题中的系统不仅是周期时变的,而且是非最小相位的. 表2~3说明基于时变和循环累量的定阶方法(与直接判定统计量相比较)具有很好的数值稳定性,且每次运算都能给出准确的阶数估计(q=imax=2). 在实验中,尽管信噪比较低,但是所用的数据长度较大(与传统的二阶统计量方法和累量方法比较),这是因为循环统计量具有较大的估计方差. 六、结束语 |
- 相关推荐
- 热点推荐
- 周期
-
什么是智能影像辨识系统?2023-06-15 835
-
伺服系统的离线惯量辨识方法介绍2023-03-01 2823
-
RM云台黑箱系统辨识及建模 精选资料分享2021-08-18 1561
-
系统辨识的详细资料说明2019-04-09 1000
-
IPMSM电感辨识算法及变参数MTPA控制2018-02-06 2567
-
模糊系统辨识仿真程序2017-12-06 558
-
闭环系统频域测试及辨识2017-10-04 1682
-
系统辨识实验报告2017-06-12 1514
-
基于Levinson_Durbin算法的变采样周期调度_戴小溪2017-03-18 588
-
基于Labview的气动伺服系统辨识2016-04-19 3280
-
求基于LabVIEW的系统辨识仪设计2012-11-18 2385
-
被动变采样周期网络控制系统的H∞控制器设计2009-07-30 649
全部0条评论

快来发表一下你的评论吧 !

