

基于Radon-STFT变换的含噪LFM信号子空间分解
嵌入式设计应用
描述
基于Radon-STFT变换的含噪LFM信号子空间分解
由于线性调频信号占有非常宽的频带,用奇异值分解就不能将含噪线性调频信号分解成信号子空间和噪声子空间.针对这一缺陷,本文提出了一种基于时频面旋转的含噪线性调频信号的子空间分解算法.文中分析了算法的性质,并提出了“伪信号子空间”的概念和用于检测直线倾角的Radon-STFT变换.理论分析和仿真实验的结果表明了这种子空间分解方法对一类含噪线性调频信号是可行的.
关键词:奇异值分解;伪信号子空间;时频分布;Radon-STFT变换;时频面旋转
Subspace Decomposition for Noisy LFM Signal Using Radon-STFT Transform
ZOU Hong-xing,ZHOU Xiao-bo,LI Yan-da
(Dept.of Automation,Tsinghua University,State Key Laboratory of Intelligent Technology and Systems,Beijing 100084,China)
Abstract:Since the LFM signal occupies a wide band in frequency domain,it's impossible to use singular value decomposition to separate the noisy LFM signal into signal subspace and noise subspace.To counter this drawback,a new subspace decomposition algorithm based on the rotation of time-frequency plane is presented in this paper along with its corresponding performance.A new concept,namely,the“pseudo signal subspace”,and a new transform for detecting the tilting angle called Radon-STFT transform are proposed.Theoretical predictions and simulation results indicate that the strategies advocated are feasible for denoising a class of LFM signals.
Key words:singular value decomposition;pseudo signal subspace;time-frequency distribution;Radon-STFT transform;rotation of time-frequency plane
一、引 言
解线调法是一种专门估计线性调频(linear frequency modulation,简称LFM)信号参数(即起始频率f0和线性调频率r)的方法[1],然而该方法失却了LFM信号的调幅(包络)信息.文献[2]提出了一种基于Radon-Wigner变换的LFM信号的滤波方法,但该方法存在两个明显的缺陷:(1)用于抽取单频正弦波的窄带滤波器的带宽对噪声抑制特性影响甚大,信号的带宽愈大,则重构出的信号中噪声含量愈显著;(2)窄带滤波器的设计需要在设计者的干预和指导下完成,算法无法自动实现这一设计过程.受文献[2]的启发,并为了克服其缺陷,作者曾提出一种增强LFM信号的时变滤波算法[3],其核心思想是:首先,求出含噪LFM信号的瞬时频率,并由瞬时频率确定信号在时频平面上的倾斜角度;其次,根据这一倾斜角度,旋转含噪LFM信号的短时Fourier变换(STFT),使得LFM信号成份的时频分布与时间轴平行;然后对旋转后的时频分布进行奇异值分解(SVD),用低有效秩分离开信号和噪声子空间;最后反向旋转信号子空间,经短时Fourier逆变换,得出滤除掉噪声的LFM信号.这种确定旋转角度方法的不足之处在于瞬时频率的估计受噪声影响较大;当信噪比(SNR)过低时,很难正确地估计出瞬时频率.显然,若旋转角度估计不准确,则旋转后的时频平面的奇异值衰减就会变慢,用低秩逼近就会丢失信号的许多细节信息,导致重构出的信号产生较大的失真.此外,当量测信号中存在多个具有不同调频率的LFM信号时,就不可能通过求瞬时频率的途径拟合出旋转角度.本文提出一种Radon-STFT变换,该变换能鲁棒(robust)地确定LFM信号在时频平面上的倾斜角度,因而可以有效地克服文[3]的缺憾.
二、适用于含噪LFM信号的子空间分解算法
本文考虑具有如下形式的叠加波形
x(t)=s(t)+n(t) (1)
其中n(t)是i.i.d的加性实值白噪声,s(t)是实值LFM信号
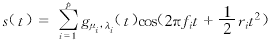 (2)
(2)
上式中gμi,λi(t)是高斯包络.定义x(t)的STFT为
STFTx(t,f)=∫+∞-∞x(u)h*(t-u)e-j2πfudu (3)
其中h为归一化窗函数,且满足‖h‖2=1.由于STFT是一种线性变换,显然有
STFTx(t,f)=STFTs(t,f)+STFTn(t,f) (4)
成立.
1.Radon-STFT变换的定义
为准确检测LFM信号在时频平面上的倾斜角度,本文仿照Radon-Wigner变换,提出了Radon-STFT变换.Radon变换是一种积分投影变换,任意二维函数f(t,ω)的Radon变换为[1,2]
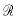 [f(t,ω)]=∫PQ线f(ucosα-vsinα,usinα+vcosα)dv (5)
[f(t,ω)]=∫PQ线f(ucosα-vsinα,usinα+vcosα)dv (5)
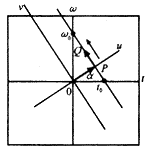
这里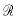 表示Radon变换,其积分路径如图1所示.
表示Radon变换,其积分路径如图1所示.
|
图1 Radon变换的积分路径 若用信号x(t)的STFT取代函数f(t,ω),则所得到的Radon变换就是信号x(t)的Radon-STFT变换(Radon-short-time-Fourier transform),用符号RSTFTx(u,α)表示,即 RSTFTx(u,α)= 当u′=u时,Radon-STFT变换的积分路径即为PQ线.
由式(7)求信号x(t)的Radon-STFT变换,并以参数(r,f0)表示其积分路径,则有
式(9)表明,若x(t)是参数为f0和r的LFM信号,则积分值最大;而当参数偏离f0与/或r时,积分值迅速减小,即对一给定的LFM信号,其Radon-STFT变换会在相应的参数(f0,r)处呈现尖峰.由于Radon变换是以旋转角度α和半径u为参数的,因此,通过检测Radon-STFT变换的最大值位置,即可确定STFT时频平面中的直线倾角.
这里H表示共轭转置,Σx=diag(σx1,σx2,…,σxr),相应的奇异值满足σx1≥σx2≥…≥σxr≥0,r=rank(Ax).信号/噪声子空间分解,就是用Ax的低秩矩阵Axk去逼近As, Axk=UΣxkVH (11) 其中Σxk是通过在Σx内令除去k个最大的奇异值以外的所有其它奇异值都等于零后得到的对角阵.记Σs=diag(σs1,σs2,…,σsr)为信号子空间的奇异值,Σn=diag(σn1,σn2,…,σnr)为噪声子空间的奇异值,并且有σxi=σsi+σni,1≤i≤r.若噪声是i.i.d的,则σn1=σn2=…=σnr.为了有效地恢复信号的时频分布,就需要从σxi中去除σni,因此如何估计σni,或等效地,如何估计Σx的有效秩,即成为问题的关键.不妨设估计出的有效秩为k,则σxk为一阈值,前面的k个奇异值对应于信号子空间,后面的r-k个奇异值对应于噪声子空间,因此问题归结为如何有效地估计阈值σxk,以保证重构信号的精度. wi=θi+δzi (12) 其中δ>0为噪声方差,zi服从标准正态分布,即zi~N(0,1).
定义3 硬阈值变换定义为
前文述及的低有效秩重构信号的出发点显然是硬阈值变换,因此本文仅讨论在硬阈值变换下的信号重构问题.有关软阈值变换的理论分析,本文不拟介绍.
其中M为采样点数,‖.‖22,M为L2范数.
这里θ=(θ1,…,θM),
证明 设
其中“。”为映设或操作算子,ISTFT为短时Fourier逆变换. E‖ 再根据定理1即得式(17)成立.定理2证毕. z(t)=x(t)+ 其中
上式中p.v.表示积分的Cauchy主值[7];
其中Tβ表示旋转β°;
由于 STFT′z(t,f)=T-β[ 其中T-β表示反向旋转β°;
与基于Cohen类双线性时频分布的信号重构方法相比,式(25)所示的信号重构方法省去了相位优化过程.这是因为STFT保留了原信号的相位信息,而Cohen类的双线性时频分布则舍弃了相位信息.这也是作者考虑构造Radon-STFT变换的另一个原因. 三、仿真实例 |

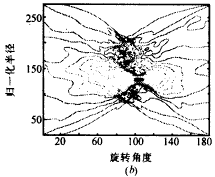


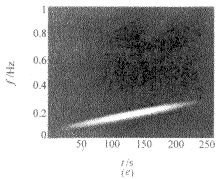
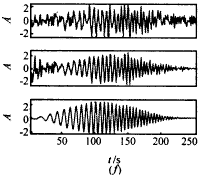
|
图2 含噪LFM信号子空间分解算法的计算过程及相应的滤波结果 四、结束语 |
-
宽带信号子空间谱估计修正方法的研究2009-05-25 508
-
LFM信号调频斜率的双正交Fourier变换分析算法2009-11-13 920
-
基于多尺度线性调频基信号稀疏分解的多分量LFM信号检测2010-02-10 953
-
关键基于二维小波变换的图像矢量分解消噪方法2010-08-10 1156
-
WVD和STFT的定义及变换原理2009-03-01 24578
-
傅里叶变换与小波变换在信号去噪中的应用2011-03-18 3663
-
宽带LFM信号到达角估计2011-05-16 868
-
小波变换去噪处理在曲面重构中的应用2011-05-19 791
-
基于小波变换的信号滤波和去噪研究2011-08-03 1333
-
radon变换在低信噪比图像中的线段检测2012-03-16 1012
-
基于Morlet小波的LFM雷达信号到达时间估计2017-12-21 1291
-
一维信号小波阈值去噪2018-01-10 8042
-
空间谱估计与MUSIC算法仿真2019-11-12 3736
-
时频分析之短时傅里叶变换STFT资源下载2021-04-26 1011
-
短时傅里叶变换特点 短时傅里叶变换的意义2023-09-07 2998
全部0条评论

快来发表一下你的评论吧 !

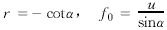 (8)
(8)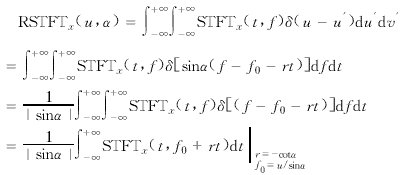 (9)
(9)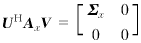 (10)
(10)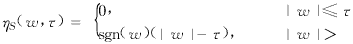 (13)
(13) (14)
(14)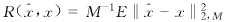 (15)
(15)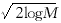 的阈值序列,则硬阈值估计为
的阈值序列,则硬阈值估计为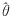 i=wiχ|wi|>lMδ,其中χ为特征函数,lM~2logM,并且
i=wiχ|wi|>lMδ,其中χ为特征函数,lM~2logM,并且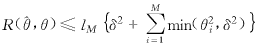 (16)
(16) (t)为x(t)的估计.对x(t)的短时Fourier变换STFTx(t,f)作硬阈值变换,然后通过短时Fourier逆变换得重构信号
(t)为x(t)的估计.对x(t)的短时Fourier变换STFTx(t,f)作硬阈值变换,然后通过短时Fourier逆变换得重构信号 (t),因之有如下定理.
(t),因之有如下定理.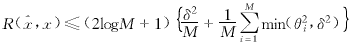 (17)
(17)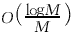 同阶,从而保证了重构信号的精度.
同阶,从而保证了重构信号的精度.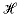 [x(t)] (20)
[x(t)] (20)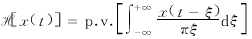 (21)
(21)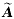 z.这一旋转过程可表示为
z.这一旋转过程可表示为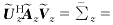
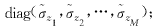
 z2=
z2=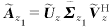 (23)
(23)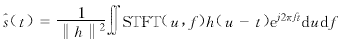 (25)
(25)