

基于Altera FPGA的的小数处理方法实现与研究
可编程逻辑
描述
作者:朱彦华,刘仲寿,张志敏,常方飞
1 引 言
发射光谱层析(EST)技术是一种不干扰原待测场分布的测量诊断技术,他在热物理量测试、等离子体诊断等方面显示出了极大的优越性,尤其是在场分布测量方面,几乎是其他方法不可替代的,是测量三维流场内部物理量分布的一种常用方法。
传统的层析重建技术,通常是利用软件编程在计算机上直接完成,这要花费很长的时间,无法满足实时重建时对速度的要求,现在已有研究者开始着手研究在硬件(例如FPGA和DSP)上来实现层析重建技术,例如:在FPGA上实现ART算法。但是,由于ART算法在重建图像时对噪声的抑制能力较差,迭代格式复杂,且有除法运算,用FPGA实现起来较为复杂。同时迭代重建算法--SIRT能够有效抑制测量误差的影响,迭代格式简单,得到广泛应用,但该法用FPGA(现场可编程逻辑门阵列)来实现时,牵涉到小数运算问题。因为在FPGA中数据都是以二进制形式参与存储、运算的,小数计算问题是FPGA应用中的一大难点,目前业界用FPGA来处理小数大都采用定点处理,这种方法行之有效,但应用范围很有限,对于在层析重建中的小数,采用定点运算是无法处理的。
本文提出一种处理小数的方法,即把将要参与运算的数据转化为IEEE标准754的二进制单精度浮点数,然后调用Altera开放的浮点数运算IP核对数据进行运算,Altera提供的IP核是Altera公司经过严格测试和优化过的电路功能模块,在设计项目时调用IP核既减少了设计中的工作量,又在一定程度上节省了芯片资源,为迭代层析实时重建提供了可能。SIRT算法较ART算法迭代格式简单,且更易减小重建误差,提高重建速度,更适用于实时重建。FPGA在设计时采用Verilog编程和调用Altera的开放IP核相结合的方法来实现,软件设计和综合模拟仿真在QuartusⅡ5.1开发平台中完成,最后给出了一些模块仿真的波形。
2 SIRT算法
SIRT算法的迭代格式为:
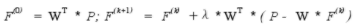
其中P是测量数据,WT是投影矩阵W的转置,λ为松弛因子,F是重建量。
物理意义为:取测量向量的反投影作为初始图像,在求k+1次估计F(k+1)时,利用k次估计F(k)加上校正图像。校正图像正比于第k次估计的误差矢量的反投影WT*(P-W*F(k))。因而每个像素的校正值实际是通过该像素的所有射线和的误差值之累加,而不是只与一条射线有关,这也是SIRT能有效地抑制测量数据中噪声的根本原因。由于每一像素的校正值是所有过该像素射线的共同贡献,一些随机误差被平均掉了,因此SIRT的校正过程被称为逐点校正。其中松弛因子的选取,会对误差收敛曲线产生影响,如果环境不变,松弛因子可以固定。 3 IEEE754对浮点数的规定
标准浮点数字长由一个符号位S、指数E和无符号(小数)的规格化尾数M构成。其格式如下:

考虑一个由一位符号位,E=8位指数宽度和M=23位的尾数(不包括隐藏的1)组成的浮点数表达式。现在来研究545.2510在单精度浮点数格式下的表达形式。由bias=2E-1-1计算偏移量如下:

定义二进制浮点数算法的IEEE754-1985标准还定义了一些其他有用的特殊数的处理,例如溢出和下溢。指数E=Emax=1…12与0尾数m=0组合是为∞保留的,0是用0指数E=Emin=0…02和与0尾数m=0编码的,注意由于有符号尾数表达式、正零和负零编码是不同的,在IEEE754标准中还定义了两个特殊数,但在FPGA浮点数算法中通常都不支持这些其他的表达式。这些其他数字是非正规数和(denormal)NaNs(not a number,非数字)。
4小数的预处理
IP核来计算数据时,输入数据和输出数据都应为IEEE标准754的二进制单精度浮点数,这样就要求在进行浮点数运算之前,先要对数据进行处理使测量值P和投影矩阵W的值转化为IEEE标准的二进制浮点数。
预处理步骤如下:
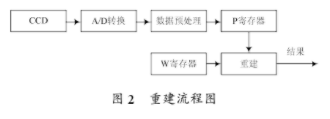
(1)对于测量数据P,他是由CCD采集并经10位A/D转换,使测量数据转换为10位二进制整数,然后经过数据预处理模块,把数据处理转化为IEEE标准754的二进制单精度浮点数,输入到外部寄存器P等待调用。
(2)对于投影矩阵W,如果图像大小一定,则投影矩阵W也是固定的,可先由Matlab仿真生成并处理转化为IEEE标准754的二进制单精度浮点数,然后存到W寄存器,等待调用。
在此只讨论由FPGA处理的部分,即只讨论对测量数据P的预处理,而对于W矩阵的值则可由Matlab编程处理完成,在此不再赘述。
流程图如图2所示。
5模拟与仿真
对于测量值P,他是由面阵CCD采集,并经有自制的10位A/D转换得来的二进制整数,根据其数据特点,可以采用移位,然后按规律重组就能将其变为IEEE标准754的二进制单精度浮点数。
5.1预处理P的模块
测量数据P为二进制整数,将其转化为IEEE标准754形式,只需要先对数据进行检测,若数据为正则符号位S=0,否则S=1;然后找出为“1”的最高位,设为“1”的最高位为第L位,则保留P[L-1:0]作为IEEE标准754的尾数M的高位,然后在其后补“0”至23位,即得尾数M;而L的值即为指数e,则E=e+127。假设P[9:0]=0001011011,则为“1”的最高位为P[6],保留P[5:0]作为尾数M[22:0]的高位,然后在后面补“0”,即得尾数M,在此M=01101100000000000000000,而指数e为6,则E[7:0]的大小为E=e+127,在此即为133,即为二进制的10000101,此处为S=0,则P转化后的值为Pout[31:0]=01000010101101100000000000000000,仿真结果如图3所示。
显然仿真结果是正确的。
按照IEEE标准754形式,把测量所得数据P和投影矩阵W的值预处理转化为IEEE标准754形式以后,即可进行运算。

5.2 浮点加法器的实现
两浮点数相加,设两个IEEE标准754单精度浮点数分别为01000000011000000000000000000000和01000000010000000000000000000000,即为十进制的3.5和3,调用浮点加法IP核,仿真波形图如图4所示。

由仿真波形图可见相加结果为01000000110100000000000000000000,即为十进制的6.5,显然结果是正确的。
5.3 浮点乘法器的实现
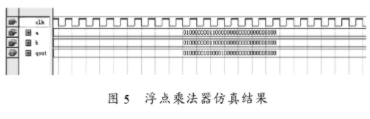
两浮点数相乘,设两数均为01000000011000000000000000000000,即为十进制的3.5,调用浮点数乘法IP核,进行仿真。仿真结果如图5所示。
由仿真波形图可见两数相乘结果为01000001010001000000000000000000,为十进制数的12.25,即结果是正确的。
6 结 语
通过以上讨论分析,本文提出的基于FPGA的处理小数的方法是可行的,不仅解决了在FPGA上实现发射光谱层析SIRT算法时的小数问题,同时也拓宽了FPGA的应用范围,使得FPGA不只能处理整数还可以处理小数,突破了以往FPGA处理小数时只能用定点处理的限制,同时本文巧妙地利用了经过严格测试和优化的Altera开放的IP核并结合自编Verilog程序,这样既减少了设计中的工作量,又可以在一定程度上节省硬件资源,提高系统运行速度,向发射光谱实时层析重建迈了有意义的一步。
责任编辑:gt
-
Altera FPGA CPLD学习笔记2021-09-18 1555
-
为什么研究浮点加法运算,对FPGA实现方法很有必要?2019-07-05 4035
-
一种基于FPGA的DSU硬件实现方法2019-06-28 2739
-
基于DSP的FPGA配置方法研究与实现2017-10-19 1370
-
面向特种LCD图像处理方法与FPGA实现研究2016-09-18 744
-
基于FPGA的数字信号处理算法研究与高效实现2016-08-29 800
-
基于FPGA的心电信号处理研究与实现2015-10-30 616
-
Altera FPGA的选型及开发2012-08-15 1481
-
FPGA实现小数分频器2011-11-29 819
-
用FPGA实现共轭变换图像处理方法2011-11-24 831
-
基于FPGA的小数分频实现方法2011-11-09 1093
-
基于FPGA的数字收发机信号处理研究与实现2011-11-01 553
-
基于FPGA的人工神经网络实现方法的研究2009-11-17 1427
-
altera fpga/cpld设计2009-07-10 768
全部0条评论

快来发表一下你的评论吧 !

