基于改进FDTD和等效计算区域分解的辐射场反演综合计算电磁方法

在研发大型军用雷达如空对地雷达，火控雷达，民用气象雷达等产品过程中经常遇到雷达附近的电磁辐射干扰问题，需要对其周边的不规则的辐射场进行精确的电磁场强反演还原，以排除其干扰。在通用的计算电磁学方法不能解决问题的情况时，针对这类非对称特定场景的电磁场分布计算还没有高效、快速、准确的计算方法的前提下，宇能无线公司提出一种基于改进FDTD和等效计算区域分解的辐射场反演综合计算电磁方法， 实现某类发射场周围特定区域任意点的时域近场分布计算、近-远场电磁变换计算和电磁图形显示。该法保障了高效的计算效率和精准的计算精度，同时也有效地减小了计算内存消耗。

1. 技术现状和面临的难题与挑战

计算电磁学领域中最常用的数值计算方法主要有三种，分别为：时域有限差分（finite-difference time-domain, FDTD）法，有限元法（finite element method, FEM）和矩量法（method of moment, MoM）。随着人们在电磁学领域研究的不断深入，电磁工程问题主要呈现出宽频带化、复杂化的特点。这就对数值方法提出了两个方面的要求：一方面，直接在时域对宽频带特性的时变电磁现象进行分析和计算；另一方面，实施简单，具有普遍性。正是由于同时具有这两方面的优点，针对要解决的具体问题，本项目研究的高频不规则的辐射特点，FDTD法可更适用于该类复杂电磁问题的求解。

尽管电磁场的感应场-辐射场计算方法已开展了大量的研究，然而，高频辐射且不规则电磁场的场分布计算在现阶段仍面临着难题与挑战，主要体现在以下几个方面。

第一方面，目前，一般延伸线的场分布计算大多数是远场计算。高频辐射且不规则电磁场感应场-辐射场场分布这一特定场景，其时域近场计算及特征分析鲜有报道。

第二方面，求解电磁场分布问题的数值方法大部分都是传统FDTD、MoM、FEM等方法。而对于非对称结构，其网格划分存在轴线上网格远多于其他方向的网格的问题，不易求解。而且常规方法需求内存消耗以保证其计算精度与计算效率。所以有必要对此类改进方法深入研究如何保证较低内存消耗的同时，也保证其有效的计算精度与效率。并进一步扩展数值方法在电磁学领域的应用。

第三方面，大型雷达周边瞬时脉冲频谱范围大，基于谱域分解的有限元方法难以适用。而时域有限元方法同样计算复杂且受时间稳定性条件限制。

2. 基于改进FDTD和等效计算区域分解计算方法

为解决大型雷达周边瞬时脉冲电磁场分布计算问题，提出一种基于改进FDTD和等效计算区域分解的反演计算技术，实现空间时域电场分布计算、近-远场变换电磁计算以及电磁图形显示。该计算方法的流程具体如下图所示：

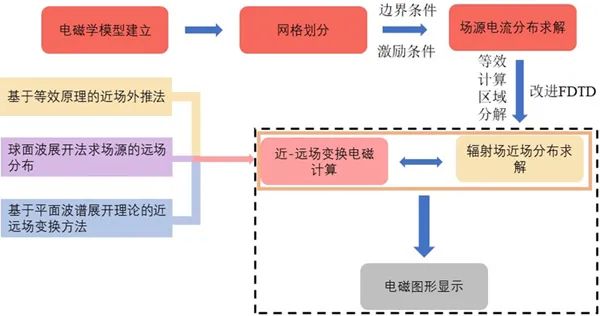
图2-1、基于改进FDTD和等效计算区域分解的反演计算技术流程图

2.1. 基于节点变量区域分解的WLP-FDTD法

传统无条件稳定WLP-FDTD法通过将WLP作为时域基函数，将麦克斯韦旋度方程中的电场和磁场分量分别展开，再使用伽略金法加权求内积，消除时间项后用中心差分格式离散所有场分量的空间导数。通过以上步骤，得到以下两个电场分量的隐式求解方程：

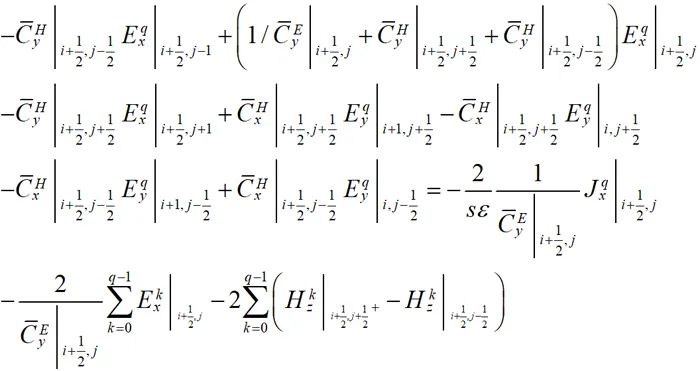
  (2-1)

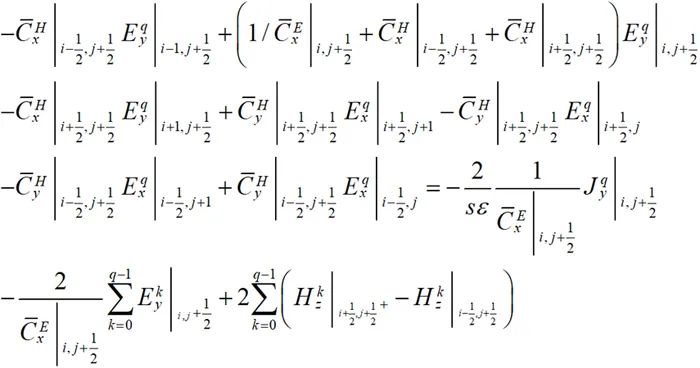
  (2-2)

其中每个电场与其周围的6个电场相互耦合，构成一个线性方程组进行联立求解。场分量的分布如图2-2所示。该线性方程组的每一行只含有7个非零元素，是一个稀疏阵。通过将(2-1)和(2-2)写成如下的矩阵形式：

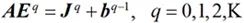 (2-3)

其中，A为系数矩阵，Eq为待求的场分量，Jq为已知的激励源，bq-1为所有低阶已知场分量的和。计算得到的电场Eq只是每个场分量在计算空间中任意一点以WLP为基函数展开式中的系数。要得到计算区域中任意一点的时域场信息，需将这些系数代入展开式中即可求得具体场值。

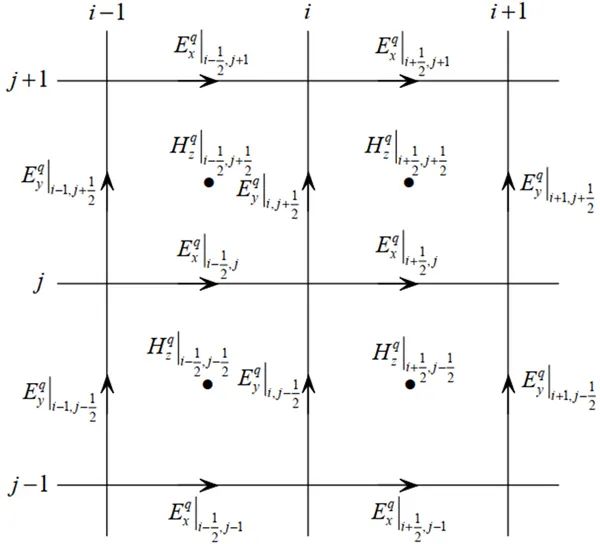
图2-2、TEz波情况下WLP-FDTD电场和磁场分量在空间的分布

无条件稳定WLP-FDTD方法尽管在计算效率上相比其他FDTD已有较大提升，但其产生的大型稀疏矩阵仍有进一步优化的空间。对此，基于节点变量的子区域划分思想，我们提出了一种更普遍和高效的区域分解技术，将隐式无条件稳定WLP-FDTD产生的大型稀疏矩阵划分成若干个互不耦合的小矩阵，通过独立求解每个小矩阵来提高数值仿真的效率。这种区域分解技术的优势在于，全局Schur Complement矩阵可由所有子区域的局部Schur Complement矩阵和子区域之间的耦合矩阵直接组成，因此计算效率可被进一步提升。其中区域分解思想由图2-3所示。

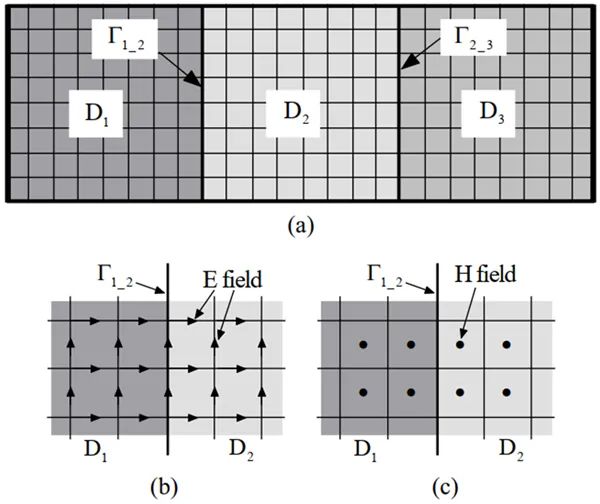
图2-3 区域分解技术示意图。(a)二维计算区域划分为三个子区域；(b)基于棱边变量的子区域划分方式；(c)基于节点变量的子区域划分方式

在基于节点变量的区域分解技术中，首先以均匀的正方形网格离散整个计算区域，再将计算区域划分成3个子区域，如图2-3(a)所示。对于特殊的仿真结构，可以使用非共形区域分解技术在不同子区域内部独立剖分网格，此时子区域之间的分界面需要更复杂的处理。划分子区域后，对矩阵系统的元素重新排序，依次排列所有完全属于子区域内部的矩阵元素，再将所有位于分界面上的矩阵元素放在最后面，即可得到基于节点变量划分子区域的Schur Complement系统。对于其中的任意一个子区域，局部Schur Complement系统会生成一个只包含位于分界面的场分量的方程组。因此，整个计算区域的全局Schur Complement系统可由局部Schur Complement系统与各个子区域之间的耦合子矩阵直接组成。由此可节省计算资源，提高计算效率。

2.2.  等效区域的场分布计算

传统计算电磁学方法常需利用计算区域内所有网格点计算观测面位置的场分布。尽管全局计算区域(Global Calculation Area, GCA)保证了良好的计算精度，但影响了内存消耗和计算效率。因此，研究了一种等效计算区域(Equivalent Calculation Area, ECA)优化划分与辐射场场分布计算方法，以此提升算法综合性能。

2.2.1. GCA场分布计算

时域辐射场观测面计算区域模型中时域辐射场分布观测区域为高频中心轴线周围一定半径的柱状区域，该半径分别为0.3m、0.5m、1m和10m。时域辐射场观测面可假设为整个柱状区域沿高频部分的剖分。因此，根据近场分布计算相关内容，观测面上的时域辐射场场分布计算为：

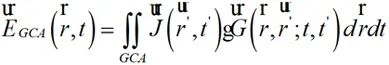
 (2-4)

其中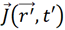，为第t'时刻高频线上的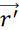位置矢量处的电流密度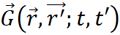，为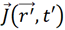第t时刻映射至时域辐射场观测面的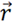位置矢量处的格林函数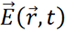，为第t时刻时域辐射场观测面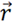位置矢量处的该点处的电场强度。GCA为整个电缆结构的全局计算区域。

然而，一方面，半径为1m和10m的柱状观察区域极大，大量网格的剖分十分不利于内存消耗和计算效率。这对仿真验证研究工作的开展将有极为严峻的挑战。另一方面，设一个区域长/宽/厚尺寸约为800mm×10mm×0.5mm，其长宽比和长厚比高至80和1600，使得沿轴线上的网格剖分增多。因此，GCA场分布计算法难以适用于高频分布的辐射场场分布计算。

2.2.2 ECA优化划分与场分布计算

ECA网格综合优化划分影响着辐射场场分布计算精度。最优ECA划分可按照下列方法求取。

一方面，根据式(2-4)，基于ECA网格划分的时域辐射场观测面上的场分布计算为：

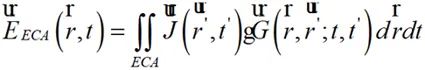
 (2-5)

如图2-5所示。以ECA网格长为参量扫描，将计算网格划分为ECA1,ECA2,⋯,ECAN。各场分布差量计算为：

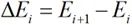 (2-6)

其中：

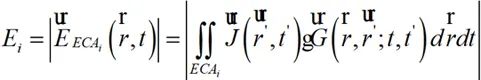
 (2-7)

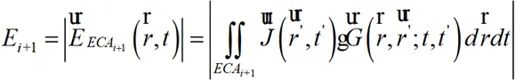
 (2-8)

式中i=1,2,⋯,N-1。当ΔEi无限逼近于0，此时ECAi和ECAi+1网格划分可认为是最优ECAopt。此时，时域辐射场观测面上的场分布计算为：

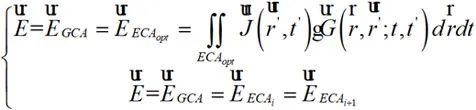
 (2-9)

另一方面，可考察ECA场分布计算与GCA场分布计算差量：

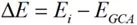 (2-10)

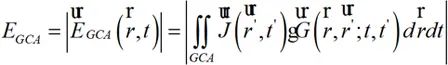
 (2-11)

式中i=1,2,⋯,N，当ΔE无限逼近于0，此时可认为ECAi网格划分是最优的ECAopt。

ECA场分布计算可将全局计算区域等效为有效计算区域，ECA最优划分可对不同柱状观测区域的场分布再次计算提供最优计算区域，以此提高计算效率，减小计算内存损耗。

2.3 近-远场变换电磁计算

2.3.1基于等效原理的近场外推法

为了根据以上方法在近场有限区域计算所得的电磁场，可利用等效原理与惠更斯原理进行近场外推计算，从而获得远区的辐射场。基于等效原理的近场外推法是先在场源周围引入外推数据储存边界面A，如图2-4所示。假设A面外为自由空间。如果保持界面A处场EH的且向分量不变，而令A面内的场为零，根据唯一性定理，这种情况与原始情况在分界面A以外的场分布不变，A面处的电场与磁场用EA、HA表示。

根据边界条件与等效原理，A面处的等效面电流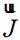和等效面磁流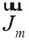，由以下公式计算获得：

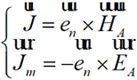 (2-12)

式中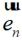为分界面A的外法向。原问题变为A面处面电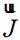流和面磁流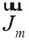在全空间为自由空间时的辐射问题。

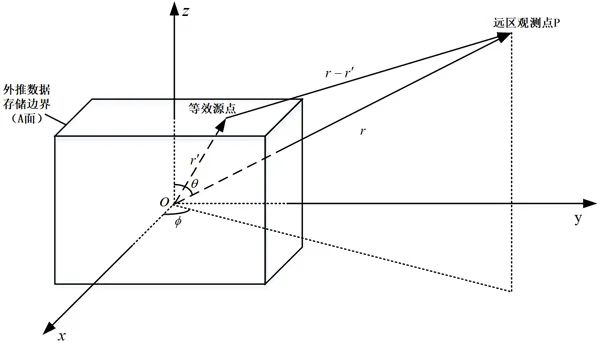
图2-4、由数据存储边界外推远区场示意图

对于时谐场情况，均匀介质汇总存在电流与磁流时的麦克斯韦方程为：

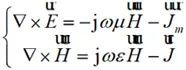 (2-13)

电流与磁流的辐射场为：

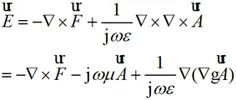
 (2-14)

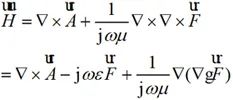
 (2-15)

其中

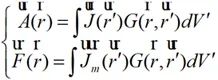
 (2-16)

式(2-16)中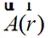和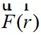为矢量势函数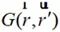；为自由空间格林函数，其中三维情况中自由空间的格林函数为：

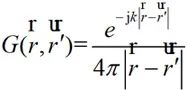 (2-17)

其中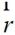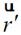，分别为观察点和等效源点位置矢量，如图1所示。可以取远区近似：

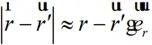 (2-18)

因此，自由空间三维远区格林函数可近似为：

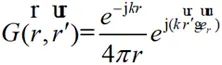
 (2-19)

将公式(2-19)代入到公式(2-16)可得：

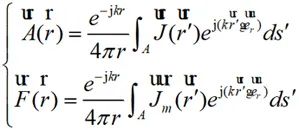
 (2-20)

对远区场可以分离出球面波因子。电流矩和磁流矩分别为：

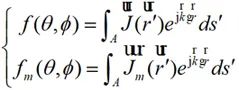
 (2-21)

公式(2-21)中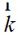，为散射波矢量：

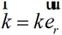 (2-22)

在远区，公式(2-14)、(2-15)可中的▽算子可以用取代，所以：

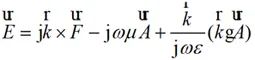
 (2-23)

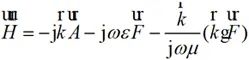
 (2-24)

将公式(2-23)右端转换为球坐标分量形式：

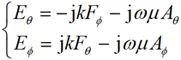 (2-25)

同理，由(2-24)式得到的远区场球坐标分量为：

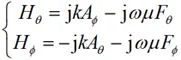 (2-26)

将(2-25)式用电流矩和磁流矩表示为：

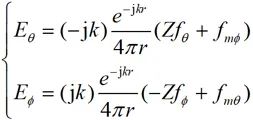
 (2-27)

其中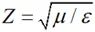为波阻抗。远区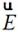和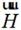的关系如同平面波。

若已知的分界面A上电场分布计算是在直角坐标系进行的，也即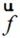、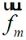是直角坐标分量。可以将公式(2-25)转换为：

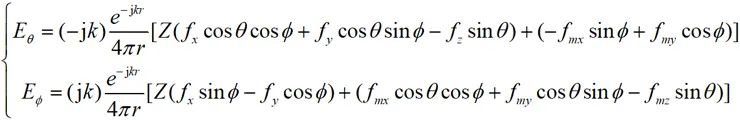
 (2-28)

根据(2-27)或(2-28)式即可求解出目标远场分布。

2.3.2 球面波展开法求场源的远场分布

运用电磁场的球面展开理论，在已知源的电流分布情况下，将自由空间中场源产生的电磁场分解为球坐标系中的标量波函数的线性组合。通过计算该求和公式中标量波函数分别对应的各项系数，从而求解出场源的远区场。

设r≥R的球面内包括了整个场源，当在r≥R的区域时的各个观测点处于无源区，电磁场是无散无旋的，在该区域的电场可以展开为球面波函数的线性叠加，表示为：

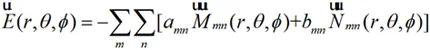
 (2-29)

式中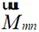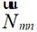，、均为矢量波函数，表达式如下所示

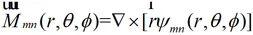 (2-30)

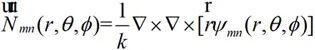
 (2-31)

上式的Ψmn是标量波函数，为齐次标量Helmholtz方程在球坐标系下的解，在无限大的自由空间中，Ψmn的表达式为：

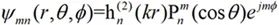 (2-32)

其中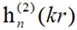，为第二类n阶Hankel函数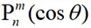，为第一类连带Legendre函数。

通过求解场强的r分量可以获得各项系数amn、bmn，如下式所示：

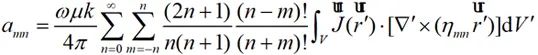
 (2-33)

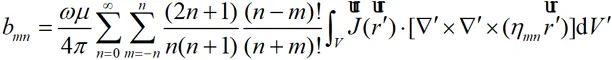
 (2-34)

其中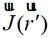，为场源的电流分布，

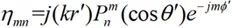 (2-35)

由公式(2-33)、(2-34)可知，系数amn和bmn均与距离r无关，因此该系数适合任何场点。将(2-33)、(2-34)代入(2-35)式即可求得无源区域的场分布。

当观测点处于场源的远场区时，由于kr→∞，则，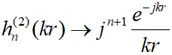

因此：

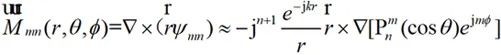
 (2-36)

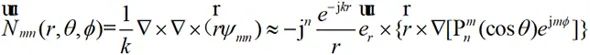
 (2-37)

将以上结果代入到(2-29)中可得：

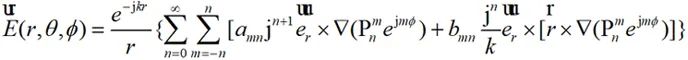
 (2-38)

因此，在已知场源的电流分布的情况下,可以计算获取在场源的远场区域内观测点的电场分布。该方法中球面波展开式的级数求和比积分求积简单，适合数值计算。

2.3.3 基于平面波谱展开理论的近远场变换方法

假设自由空间中，无源区域内某观测点的电场为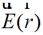，可以通过傅里叶变换在空间频域展开：

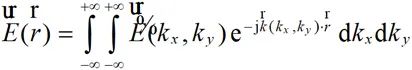
 (2-39)

其中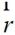，为观测点的位置矢量，kx和ky分别表示自由空间中波矢量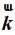的x和y分量，且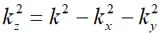。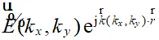为沿 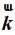方向的平面波。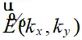为傅里叶变换后每个方向的平面波对应的频谱。上式说明，空间任意一点的电场可以表示成沿各个不同方向的平面波的积分求和。如果想要获取空间中的场，我们只需要求得观测点沿不同方向传播的频谱,即可获得该观测点的电场。

由于无源区域内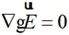,可以获得：

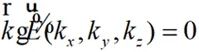 (2-40)

所以：

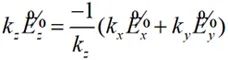
 (2-41)

假设已知在场源的近场区域内z=d1平面上的切向电场，该平面上切向电场可根据公式(2-39)表示为：

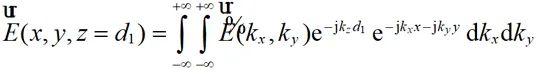
 (2-42)

因此将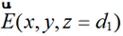进行傅里叶变换即可获得不同方向平面波对应的频谱：

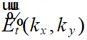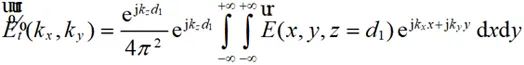
 (2-43)

将(2-43)代入(2-41)可求出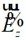，因此：

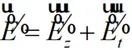 (2-44)

将公式(2-44)中计算获得的频谱代入到(2-39)中，即可获得在场源外自由空间中的电场分布。当观测点距离场源的距离r很远时，可以通过驻相法对运算进行简化。进一步的，由于当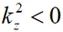，也即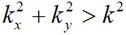时，平面波沿z轴呈指数衰减，高波数时对应的衰减更大，在计算远场时可以忽略。

3. 项目内容结果

结合电磁场中区域分解技术，将高频辐射装置分解提取出相应的几何参数，进行了负载短路周边辐射场的电磁仿真工作。

3.1. 短路负载

短路负载模型结合转接装置的内部结构和材料属性，进行如下的仿真设置：转接装置的底座部分设置为εr=2.1，tanδe=0.001的电介质材料，然后两根金属引线与短路线相连，引线的末端设置为集总端口激励。

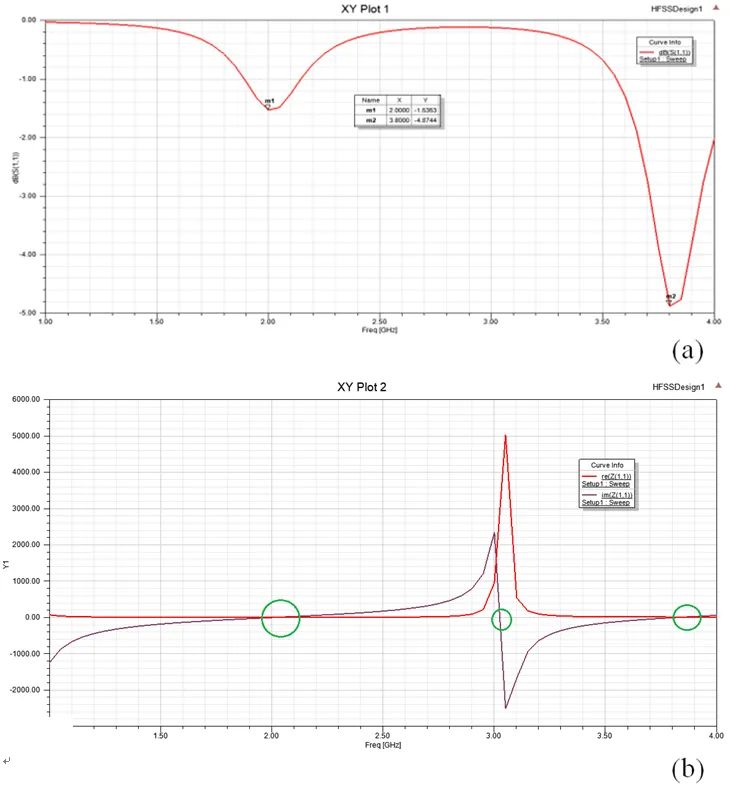
图3-1 短路负载电磁仿真（a）短路负载S11参数；（b）短路负载输入阻抗

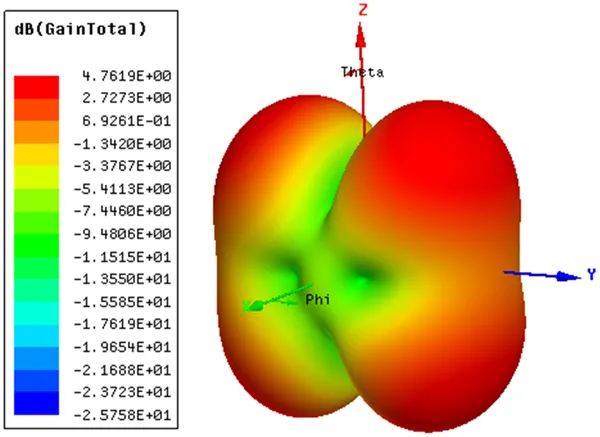
图3-2 在3.8GHz频点处的增益方向图

短路负载S11参数和输入阻抗分别如图3-1(a)和(b)所示。其中，仿真计算的频段为1～4GHz。从输入阻抗曲线上看，在1～4GHz频段内，一共出现3处输入电抗为0的频点，代表三个谐振点，其中3.8GHz处的输入阻抗与50Ω最接近。因此，可研究该频点的增益方向图，如图3-2所示。不考虑匹配效率，最大增益为4.7619dBi，倘若考虑匹配效率，最大实际增益为3.0517dBi。

3.2. 整体联合仿真

短路负载与整体结构的仿真，完成近场分布计算。该模型在Y方向上的最大长度约为6.4cm，在X方向上的最大长度为2.78cm。设中心为坐标原点O，以边长为40cm的正方体为近场观测面。若该观察面边长足够大，远大于该长度即40cm、且计算区域同样很大，如要求的1m/10m的柱状区域，那么计算如此大的区域则会占用极大的计算资源（边长60cm的正方体空气盒子占用内存超过1TB）。

表3-1远场条件和辐射增益

 

频率(GHz)	远场距离(m)	增益(dBi)	实际增益(dBi)
0.4	1.2	-8.22	-35.81
1	0.48	-1.1	-26.05
2.1	0.32	5.05	-0.77
4.1	0.32	5.32	4.05
6	0.32	5.46	3.85

 

如果以D=6.4cm作为短路负载的最大尺寸，根据天线教材上面给出远场距离条件：

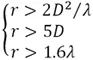 (4-1)

仿真频段为0.4～6GHz，下表即为不同频点的远场距离和增益：

该频段的S11参数曲线如图3-3(a)所示，尽管分别在2.1GHz、4.1GHz和6GHz附近存在谐振点，但输入阻抗与50Ω相差较大。将频段拓展至6.5GHz时，其输入阻抗为42.836+j5.6473Ω，S11参数小于-20dB。短路负载从2GHz开始能够进行有效的电磁辐射，增益在5dBi以上；在1GHz以下，增益非常低。整体结构的场强方向图如图3-3(b)所示，选取的频点为0.4GHz。其方向性系数是1.55dBi，即1.43，呈现为全向辐射状态，最大辐射方向出现在线圈所在平面，可等效为电小环辐射。图3-4至图3-7分别为0.4GHz、2.1GHz、4.1GHz和6GHz处的电场和磁场分布。而图3-8为不同频点下的增益方向图。从方向图的形状来看，金属线圈的周长接近于一个波长，短路负载的辐射方向图和一波长的大环天线方向图形状非常接近。

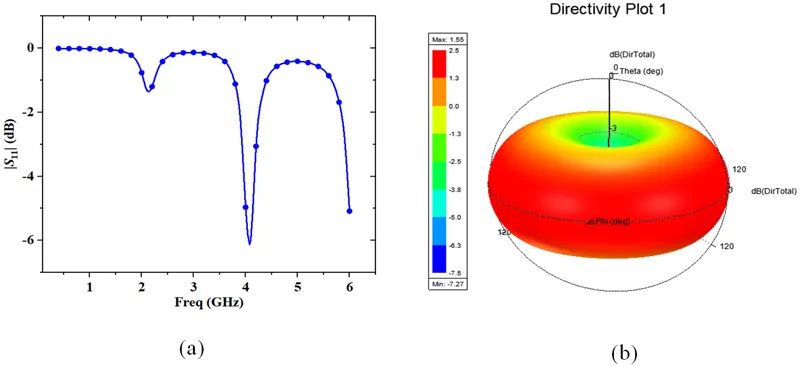
图3-3 (a)S11参数曲线；(b)0.4GHz处的场强方向图；

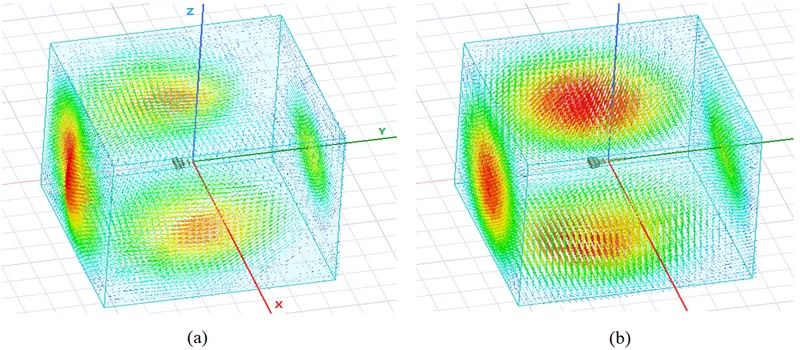
图3-4 0.4GHz处场分布。(a)电场；(b)磁场；

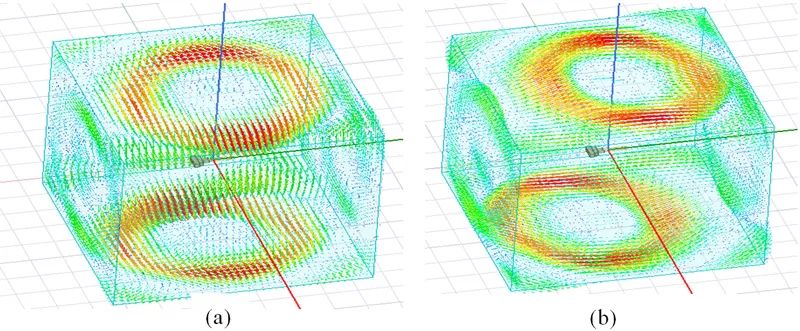
图3-5 2.1GHz处场分布。(a)电场；(b)磁场；

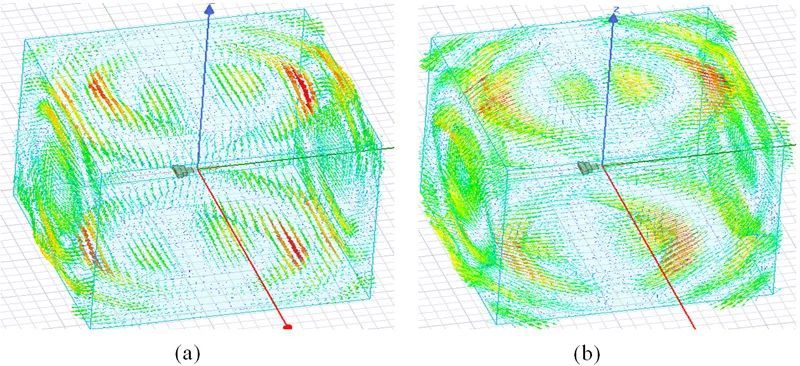
图3-6 4.1GHz处场分布。(a)电场；(b)磁场；

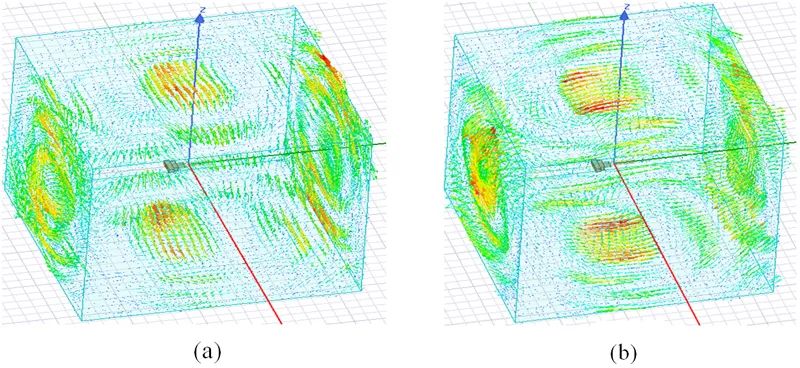
图3-7 6GHz处场分布。(a)电场；(b)磁场；

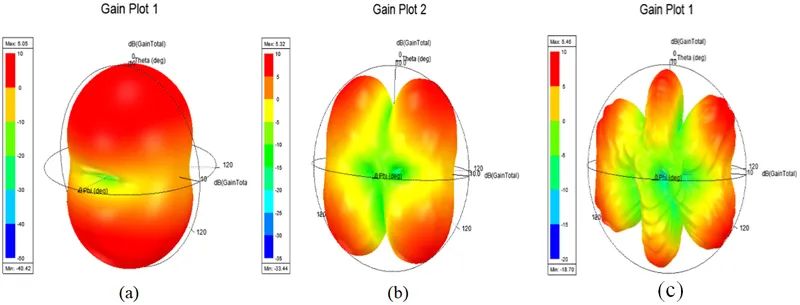
图3-8 增益方向图。(a)2.1 GHz；(b) 4.1 GHz；(c) 6 GHz

4. 技术及应用

基于此改进FDTD和等效计算区域分解的计算电磁技术能够有效反演还原大型复杂雷达系统的周边电磁场场强，分析出系统工作时对周围环境的影响，从而做出精确的反干扰或者其他规避措施，也可以用于分析被探测目标物体的电磁散射，计算出电磁场场强，建立分布模型的赋形场，从而还原出物体的电磁特性，进而进行物体的成像还原或者跟踪等上层应用。

 

原文标题：大型相控阵雷达周边复杂区域的电磁反演技术

文章出处：【微信公众号：微波射频网】欢迎添加关注！文章转载请注明出处。

责任编辑：haq