

独立分量分析在心电信号处理中的应用
嵌入式操作系统
描述
独立分量分析在心电信号处理中的应用
独立分量分析ICA(Independent Component Analysis)是近来发展起来的一种新的盲源分离方法BSS(Blind Source Separation)[1]。ICA处理的对象是一组相互统计独立的信源经线性组合而产生的混合信号,其最终目的是在源信号和混合方式都未知的情况下,从混合信号中恢复出源信号各个独立成分的过程。ICA这种能够提取独立成份的特性已被广泛应用于生物医学信号处理、混合语音信号分离、图象的消噪等方面。
人体的心电信号在采集过程中,由于仪器、人体等内外环境的影响,不可避免地混杂了各种干扰信号,如工频干扰、人工伪迹、基线漂移和肌电干扰等。这些噪声干扰与心电信号混杂,会引起心电信号的畸变,使心电波形模糊不清, 从而影响信号特征点的识别,难以分析和诊断,因此有效分离各种干扰信号对心电信号处理有着重要的意义[2]。在论文中,将采用ICA方法对心电信号进行分析处理,消除干扰信号。
1 ICA基本理论
1.1 ICA 模型
假设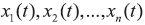 是一组N维的观测信号,
是一组N维的观测信号,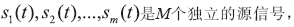 源信号通过混合以后得到观测信号,如式(1)所示:
源信号通过混合以后得到观测信号,如式(1)所示:
 素表示源信号之间的线性混合情况。
素表示源信号之间的线性混合情况。
独立分量分析就是在源信号S及混合矩阵A未知的情况下,通过求得一M×N的解混矩阵W,使得通过它可以仅从观测信号X来恢复出源信号S。其中y为源信号的估计矢量:

ICA原理如图1所示。
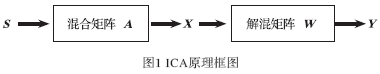
对于以上描述的ICA模型,由于源信号S和线性组合方式A均未知,如果没有任何先验知识,要想仅从观测信号恢复出源信号是不可能的。为使问题可解,一般做如下假设:
(1)各源信号之间相互统计独立;(2)源信号间的混合方式是线性的;(3)信号中最多只允许有一个高斯信号,因为多个高斯信号的线性混合仍然服从高斯分布,从而导致信号不可区分;(4)观测信号的数目不能小于独立信号源的数目,一般讨论两者相等的情况;(5)源信号的各分量均值均为零。
而且,y只是在满足上述条件下对S的逼近。换句话说,ICA算法任务的实质是优化问题。因此ICA方法的具体实现主要包括两个方面,确定优化判据即目标函数以及选择优化算法。
目标函数通常也称为对比函数或代价函数。目标函数的定义主要是确定分析的目标和建立判断是否独立的判据。ICA方法的判别依据根据度量各分量之间独立程度的判据不同, 有多种形式。如信息最大化(info-max)方法、最大熵(ME)和最小互信息(MMI)方法、极大似然(ML)法及快速ICA(fastICA)方法等。其中FastICA算法使用方便,程序编写也比较成熟,应用较多[3]。对于同一个目标函数亦可以有不同的优化算法。常见的优化算法主要有梯度法和牛顿迭代法。
1.2 FasICA算法
FasICA又称为固定点(Fixed-Point)算法,是一种基于负熵或极大似然估计等独立性判决准则的分离算法。与普通的神经网络算法不同的是,这种算法采用了批处理的方式,即在每一步迭代中都存在大量的样本参与运算。另外,该算法采用了定点迭代(Fixed-Point Iteration)的优化方式,使得收敛速度快且稳健[4-5]。
使用FasICA算法分离单个独立分量时,首先进行白化处理,使X的相关矩阵E[XXT]=1,即令X=BS,其中B是混合矩阵,其列向量是正交的。再考虑用kurtosis作为对比函数,从而使得kurtosis达到最大化得到W(W=BT)。其对比函数如下:
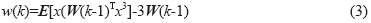
其中,w?=Wi(为W一行),且||?W||=1
具体实现过程如下:
(1)初始化权值向量W(0),令||W(0)||?=1,k=1;
(2)迭代运算:w(k)=E[x(W(k-1)Tx3]-3W(k-1),W=(bj)且||W||?=1,bj为B的第j列,其中数学期望可以用X的大量样本点的均值代替;
(3)将W(k)标准化,即W(k)/||?W(k)||;
(4)如果W(k)TW(k-1)不是足够地接近1,令k=k+1,返回步骤2,否则输出向量W(k)。算法最后给出的向量W(k)意味着分离了混合信号x(k)中的一个非高斯信号W(k)Tx(k),其中k=1,2…等于其中的一个源信号[6-7]。
对于多个独立分量,可重复使用上述过程进行分离,但每提取出一个独立分量后,要从观测信号中减去这一独立分量,如此重复,直到所有独立分量完全分离。
与其他ICA算法相比,FastICA有以下优点:(1)立方收敛,相比普通的基于梯度下降方法的线性收敛,收敛速度更快;(2)不需要选择学习步长或其他参数,更易使用;(3)不管是具有超高斯分布还是亚高斯分布的分量都能被提取出来;(4)独立成分可以逐个估计,在仅需要估计几个(不是全部)独立分量的情况下,能减少计算量。(5)FastICA还有许多神经算法的优点,如并行、计算简单、要求的内存少等。
工频干扰是由电力系统引起的一种干扰,由50Hz及其谐波构成,是心电信号中最常见的干扰源之一。可以说消除工频干扰是心电信号检测与处理过程中最经典的话题。
由于心电信号和工频干扰信号可以被看成是由不同的相对独立的源产生的,因此可以认为它们之间是相互独立的,观测到的信号混合方式是线性的;严格地说心电信号及这些干扰信号都不是高斯信号,这样就满足了ICA的前3个条件,对于第4个条件,可以通过增加通道数目来满足。因此在实验中,可以利用ICA算法来分离源信号,消除工频干扰。
工频干扰的数学模型可表示为:

其中,A, f, θ分别为工频干扰的幅值、频率以及相位。f为50?Hz,而A, θ为未知的参数,且θ通常较难估计。利用sin(2π?f?)和cos(2π?f??)的线性组合可以得到任何相位的正弦信号,因此用一个正弦信号s1(t)=sin(2π?ft)和一个余弦信号s2(t)=cos(2π?ft)正交来构造工频干扰源。
图2为原始心电信号(数据来源于MIT-BIH Arrhythmia Database,采样个数为3?000)以及所构造的工频干扰信号。将这三路信号混合后的观测信号作为FastICA算法的输入,即可分离出相应的工频干扰,分离结果如图3所示。
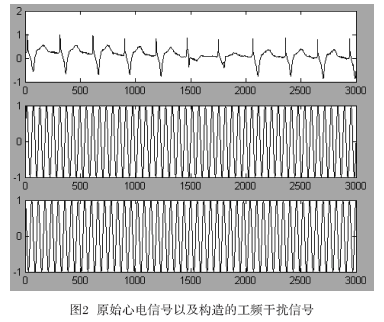
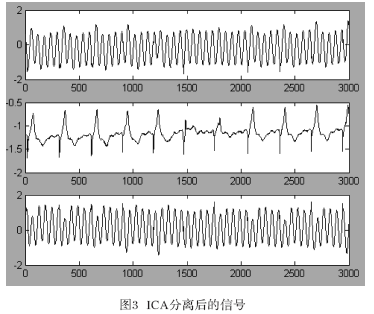
比较源信号以及经过ICA分离后的信号图,可以看到,分离出的信号除了波形的次序、极性和波幅发生变化之外,源信号的波形被很好地分解出来,能比较真实地反映源信号。可见,利用ICA方法能成功地将工频干扰消除,在没有破坏原有有用信息的基础上,还能使某些特征由于干扰的消除变的更明显。
本文将ICA方法应用于心电信号干扰消除过程,成功分离出干扰信号,较好地保留了原始心电信号中的细节信息,且不受信号频谱混迭的限制,具有良好的效果。实验证明独立分量分析方法是一种有效可行的信号分离方式,必将得到生物医学信号处理领域的广泛应用。
但作为一种新的信号处理技术,ICA理论体系并不完善,一些实际问题还有待于进一步解决。如分析各独立分量时在很大程度上依赖于人的经验,各分量的输出次序不确定,观测数目如果小于信号源数目的情况以及信号源非线性混合等情况都还需要继续研究。
- 相关推荐
- 热点推荐
- 心电信号
-
TF卡在心电监测仪中的多功能应用2024-01-29 1143
-
《心电信号采集及小波分析处理系统设计》pdf2022-02-09 1126
-
如何使用自适应滤波器解决心电信号中噪声干扰的问题2019-11-28 2315
-
心电信号检测2016-04-18 6588
-
基于FPGA的心电信号处理研究与实现2015-10-30 617
-
心电信号心电信号心电信号心电信号心电信号心电信号2014-04-18 2073
-
基于SOPC心电信号的采集与处理2012-01-16 1179
-
基于SIMULINK的心电信号源系统设计分析2010-12-16 4213
-
独立分量分析在心电信号处理中的应用2010-11-13 514
-
动态心电信号自动分析技术的研究2010-01-09 709
-
利用ARMA模型系数对心电信号的分析2009-11-30 6434
-
利用ARM的心电信号处理系统的设计2009-11-28 4997
-
心电信号采集记录系统的设计2009-07-06 1120
全部0条评论

快来发表一下你的评论吧 !

