对一种斩波运算放大器输入电流噪声的理论分析和测量

　　摘要

　　本文介绍了对一种斩波运算放大器输入电流噪声的理论分析和测量，该放大器具有 10 pF输入电容、5.6 nV/√Hz电压噪声PSD和4 MHz单位增益带宽。当配置的闭环增益更高时，输入电流噪声以输入斩波器处动态电导的热噪声为主。此外，理论分析确定了输入电流噪声的另一个来源—由输入斩波器处动态电导采样的放大器电压噪声所引起。

　　而且，在采样时，宽带电压噪声谱密度会折回到低频，使得相应的电流噪声谱密度实际上随着闭环带宽的加宽而增加，因而配置的闭环增益越小，电流噪声谱密度越大。当闭环增益为10时，测得的电流噪声为0.28pA/√Hz，但在单位增益配置时，电流噪声增加到 0.77 pA/√Hz。

　　I.引言

　　斩波技术周期性地校正放大器的失调电压，故能实现微伏级失调 电压和非常小的1/f噪声（其转折频率低于亚赫兹）。因此，许多斩波运算放大器和仪表放大器主要用于检测源阻抗和信号频率相对较低的小输入电压。其重要应用之一是放大反映光、温度、磁场、力的毫伏级传感器信号，此类信号的频率大多低于千赫兹2 然而，相比于没有斩波的传统CMOS放大器，输入斩波器的开关会引入高得多的输入偏置电流和输入电流噪声。当放大器的输入由高源阻抗驱动时，这种输入电流噪声会被转换为电压噪声，其在放大器整体噪声中可能占据主导地位。

　　文章“ 斩波放大器中输入电流噪声的测量和分析”解释了输入电 流噪声的各种可能来源，并且将与输入 MOS开关的电荷注入相关 的散粒噪声确定为主要噪声源。然而，文章“带开关输入的放大器中的额外电流噪声”将输入斩波器处的动态电导的热噪声确定为主要噪声源。在所有先前的测量中，放大器的输出电压噪声通过放大器输出到输入的反馈衰减与输入斩波器隔离。

　　虽然斩波运算放大器传统上用于高闭环增益配置，但低闭环增益 和/或高源阻抗配置也需要其低失调电压和低1/f噪声特性。因此，了解其在这些配置中的电流噪声行为十分重要。这篇文章简单介 绍了高和低两种闭环增益配置下斩波运算放大器的输入电流噪声分析和测量，参见“采用自适应时钟增强技术的5.6 nV/√Hz斩波运算放大器在轨到轨输入范围内实现最大0.5μV失调”。

　　它确定了输入电流噪声的另一个来源，即由输入斩波器的动态电导采样的运 算放大器宽带电压噪声所引起。此外，在采样时，来自斩波的偶次谐波频率的电压噪声功率谱密度（PSD）会折回到低频，导致相应的电流噪声PSD增加。因此，当闭环增益较低时，此噪声源在总输入电流噪声中可能占主导地位，使得运算放大器的输出电压噪声以较小的衰减到达输入斩波器。

　　第II部分回顾了先前报告的输入电流噪声源，第III部分解释了由采样宽带电压噪声和相关的噪声谱折叠效应引起的输入电流噪声源的机制。第I V部分对运算放大器的各种电流噪声源进行了一些数值计算。第V部分将计算出的电流噪声与仿真和测量结果进行比较，以验证分析。第VI部分提出了关于降低输入电流噪声的一些建议，文章最后在第VII部分中给出了一些结论。

　　II. 先前报告的输入电流噪声源

　　“斩波放大器中输入电流噪声的测量和分析”一文中解释了如下三种电流噪声源。第一，输入开关的通道电荷注入可以近似为平均电流Iq_ave，从而导致散粒噪声：

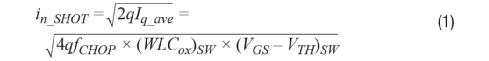
其中fCHOPP为斩波频率，而(WLCox)SW 和(VGS – VTH)SW分别为开关的栅极氧化层电容和过驱电压。   第二，时钟驱动器产生kTCC噪声电荷，其被采样到开关的栅极氧化层电容上，然后噪声电荷在每次斩波时流入放大器的输入：  

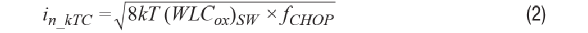
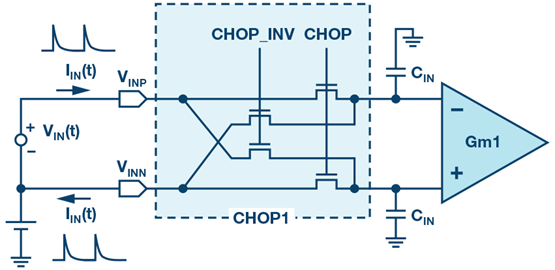
图1. 斩波和输入电容引起的动态输入电流。   第三，如图1所示，每当输入斩波器CHOP1切换时，动态输入电流IIN(t)就会流入放大器的输入电容CIN。当施加直流电压源 VIN(t) = VIN_DC时，平均输入电流IIN_ave 由下式给出：  

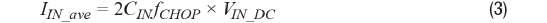
       然后，相关的动态输入电导 GIN_ave和热噪声in_GIN由下式给出：  

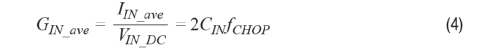
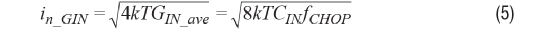
　　注意，三个噪声方程式1、2、5中的任何一个都包含一组独特的电路和开关参数，根据参数值不同，任何一种噪声都可能在整体噪声中占主导地位。在所有三个测量的放大器中（一个开环斩波仪表放大器和两个斩波运算放大器，闭环增益为100），方程式1所示的散粒噪声均在总电流噪声中占主导地位。该开环仪表放大器仅有125 fF输入电容，因此方程式5所示的动态电导的热噪声无关紧要。

　　在文章“带开关输入的放大器中的额外电流噪声”中，测量了由分立FET构成的斩波器，当添加10pF至100pF的分立电容时，方程式5所示的热噪声在总电流噪声中占主导地位。请注意，电流噪声随电容值增加而增加。 III.采样电压噪声和噪声谱折叠效应引起的电流噪声 如方程式5所暗示的，动态电导本身会产生热电流噪声，而且其采样操作还会将输入斩波器上的电压噪声转换为电流噪声。

　　采样交流输入电压引起的动态输入电流 直流输入电压下的动态输入电流由方程式3给出。现在考虑一种具有交流正弦差分输入电压VIN（t）和频率 2 × fCHOPP的情况，如图2所示。可以看出，当斩波时钟CHOP和CHOP_INV切换时，VIN（t）达到其峰值VIN_AC。因此，就像直流差分输入电压一样，该交流差分输入电压产生动态输入电流IIN（t），其平均电流IIN_ave由下式给出：

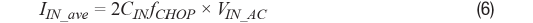
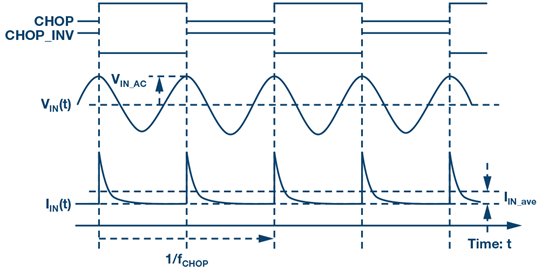
图2. 交流差分输入电压下的动态输入电流波形。  

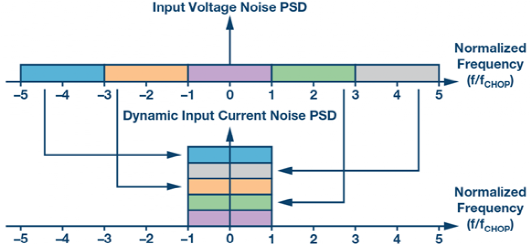
  图3. 电压噪声PSD被采样并转换为电流噪声PSD时的噪声谱折叠效应   当输入电压和斩波时钟之间的相位差是随机的时候，方程式可以使用输入电压VIN_RMS的有效值和相应的输入电流IIN_ave_RMS来重写：  

 

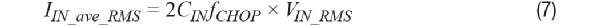
　　当以较高的斩波偶次谐波频率（例如4 × fCHOP 或6 × fCHOP）施加交流输入差分电压时，输入电流也会以相同方式出现。 采样电压噪声PSD和噪声谱折叠效应引起的输入电流噪声PSD 当输入电压的频谱包括斩波的多个偶次谐波频率时，它们全部折回到低频，这被称为噪声谱折叠效应。斩波被认为是一种调制技术，而不是采样技术。然而，此动态输入电流基于采样的输入电压而出现，不是基于连续输入电压而出现，因此会发生噪声谱折叠。

换句话说，平均动态电流量仅由斩波情况下的差分输入电压决定，而不是由任何其他时间的差分输入电压决定。 图3显示了噪声谱折叠效应，其中输入电压噪声PSD在DC到5 × fCHOP之间为enn，但在5 × fCHOPP以上为零。这就产生了DC到±fCHOP（即奈奎斯特频率）之间的输入电流噪声PSD。±fCHOP之间的输入电压噪声PSDen（fen）会贡献无频移的输入电流噪声PSDin_en_GIN_0。  

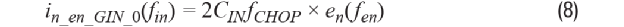
其中，fen和fin分别是输入电压噪声PSD和相应的输入电流噪声PSD 的频率。高于fCHOP且低于3 × fCHOP的输入电压噪声PSD会贡献频移 为–2 × fCHOP的输入电流噪声PSD：  

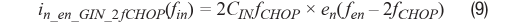
       总输入电流噪声PSDin_en_GIN_RSS(f)是通过对运算放大器闭环带宽内的所有频率折叠的PSD进行求和得到的，包括方程式8和9中的那些PSD，采用和方根(RSS)计算：  

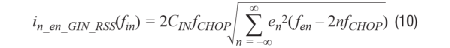
       当电压噪声PSD在en处是平坦的，并且带限频率为fen_BW,相应的低频电流噪声PSD由下式给出:  

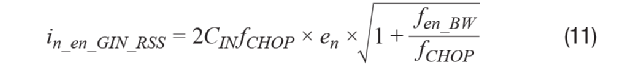
  当fen_BW/fCHOP >> 1时,方程式可近似为：  

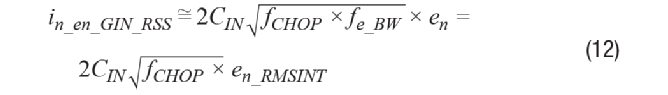
  其中，en × √fen_BW由积分有效值电压噪声en_RMSINT代替。该输入电流噪声源大致与差分输入端的有效值电压噪声、输入电容大小和斩波频率的平方根成比例。  斩波运算放大器的输入电流噪声估计  斩波运算放大器框图   本部分及后面的部分分析、仿真并测量“采用自适应时钟增强技术的5.6 nV/√H z斩波运算放大器在轨到轨输入范围内实现最大0.5µ V失调”中介绍的斩波运算放大器。

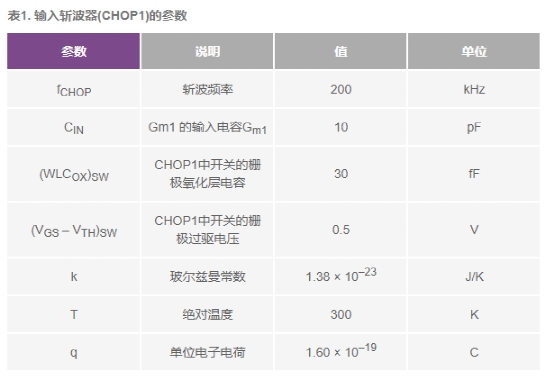
       该运算放大器采用0.35μm CMOS工艺实现，辅之以5V晶体管，实现了5.6 nV/√Hz的电压噪声PSD和4 MHz的单位增益带宽。其框图如图4所示，表1总结了输入斩波器(CHOP1)的参数。为实现轨到轨输入共模范围，输入跨导放大器级Gm11由n沟道和p沟道差分对组成，二者都会贡献输入电容CIN。此外需要较大尺寸的输入MOS器件，从而以高功效比增加Gm1的跨导。输入斩波器CHOP1中有四个开关，每个开关都是由NMOS实现，并且其栅极电压基于输入电压而自适应偏置，使得在输入电压变化时，其过驱电压恒定在0.5 V。  

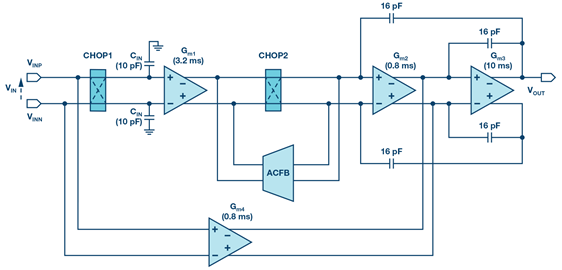
图4. 斩波运算放大器框图  

　　差分输入端上的电压噪声 为计算方程式12中所示的电流噪声PSD，需要知道积分有效值电压噪声vin_RMSINT。使用闭环增益=1、2、5、10仿真斩波运算放大器。图5（a）和（b）分别显示了运算放大器差分输入端的电压噪声PSD及其积分有效值噪声。本文中的所有仿真均由SpectreRF周期性噪声仿真（PNOISE）进行，以考虑斩波的开关效应。由于斩波，噪声PSD在100 kHz以下是平坦的，但在200 kHz的斩波频率处达到峰值。

　　请注意，这些数字表示运算放大器差分输入端的噪声，而不是输出端噪声，因此低于100kHz的噪声PSD在不同闭环增益下是恒定的。在1MHz以上，噪声PSD也会增加，并以Gm2， Gm3，和Gm4的热噪声为主，原因是Gm1的增益下降。因此，其积分有效值噪声在1 MHz以上也会增加，特别是在闭环增益较低的情况下，主要原因是闭环带宽较高。增益 = 10时，差分输入端的积分有效值电压噪声为11 μVrms，但增益 = 1时为68 μVrms。

 

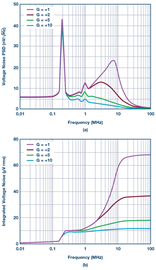
　　图5. 斩波运算放大器的仿真差分输入电压噪声 每个输入电流噪声源的估算 接下来将仿真得到的积分有效值电压噪声应用于方程式12以计算电流噪声PSD。另外，其他噪声源4引起的电流噪声PSD是通过将表1中的参数应用于方程式1、2、5来计算的。图6显示了闭环增益从1到10时计算出的四个噪声源的电流噪声PSD。当闭环增益为1和2时，采样宽带电压噪声PSD引起的电流噪声PSD（方程式12）在总电流噪声PSD中占主导地位。

它随着闭环增益提高而减小，当闭环增益为10时，其仅使总输入电流噪声PSD增加7%。相反，当闭环增益高于5时，总电流噪声PSD以动态电导本身的热噪声（方程式5）为主，故而几乎保持恒定。因此，对于该运算放大器，使用最高10倍的闭环增益来评估电流噪声即足够。 V. 仿真和测量结果 为了验证分析，将图6所示的总电流噪声PSD计算结果与仿真和测量结果进行比较。PNOISE仿真和测量均利用图7所示电路设置进行。电压噪声PSDen_OUT是通过短路RS来测量，总噪声PSDen_OUT_RS是在RS = 100 kΩ下进行测量。电流噪声PSD in_IN则由下式给出： 

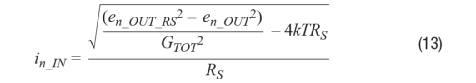
其中，(1 + RF/RG)是运算放大器周围的闭环增益，GPOST =100是后置增益，用以简化动态信号分析仪HP 35670A的测量。注意在方程式13中，en_OUT_RS和en_OUT以RSS形式减去，因为电流噪声PSD主要由较高频率的折叠噪声引起，因而与电压噪声PSD不相关。  

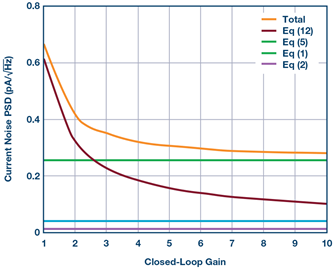
图6. 不同来源的输入电流噪声贡献计算结果  

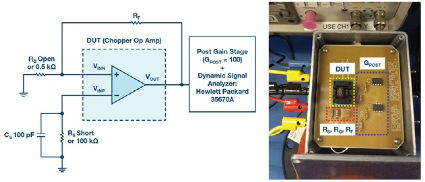
　　图7. 用于输入电流噪声仿真和测量的电路设置

　　外部电容 CS = 100 pF 将RS的噪声带宽限制在截止频率16 kHz。在这种情况下，RS的热噪声在斩波的第一偶次谐波频率（400kHz）处得到充分衰减，因此不会通过噪声谱折叠效应贡献电流噪声。另一方面，运算放大器宽带输出电压噪声达到负输入VINN， ，由输入斩波器处的动态电导采样，可能会贡献相当多的电流噪声。随后，低频中的电流噪声PSD再次被RS转换为电压噪声，此噪声可以在后置增益级的输出端进行测量。

　　图8显示了增益 = 1配置（RG开路且RF短路，如图7所示）下仿真和测量得到的全频率范围输入电流噪声PSD。在0.01 kHz时，仿真和测量得到的噪声PSD分别为0.69 pA/√Hz和0.78 pA/√Hz。然后，噪声PSD在由 RS和CS产生的16 kHz截止频率处开始下降。图9显示了不同闭环增益下0.01 kHz时的输入电流噪声PSD，以将图6中的计算 值与仿真和测量结果进行比较。仿真和测量得到的电流噪声PSD均随着闭环增益的降低而增加，与计算结果有良好的相关性。增益=10时测得的输入电流噪声PSD为0.28 pA/√Hz，但增益 = 1时提高到最大0.77 pA/√Hz。

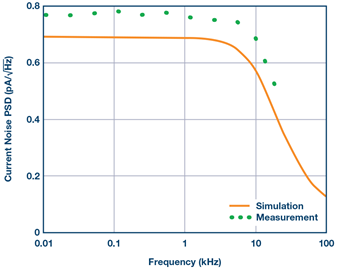
图8. 输入电流噪声PSD与频率的关系  

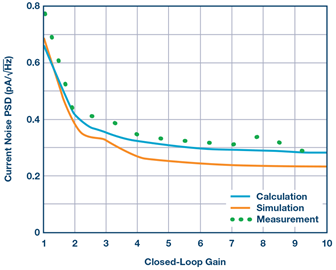
　　图9. 10 Hz时的输入电流噪声PSD与闭环增益的关系 VI. 减少输入电流噪声的建议 方程式1、2、5、12给出的所有电流噪声源都与斩波频率的平方根成比例增加。此外，与输入斩波器处动态电导相关的电流噪声源（方程式5和12）随着放大器的输入电容增加而增加。这意味着针对较低电压噪声PSD而设计的斩波运算放大器往往具有较高的输入电流噪声PSD，因为需要增加其输入器件的大小。

　　在给定源阻抗下，必须理解这种权衡才能实现最佳电压噪声和电流噪声PSD。如果可能，应避免在弱反转区下使用互补输入对或输入晶体管，以便减小输入电容。 方程式12表明，电流噪声PSD随着放大器差分输入上的积分有效值电压噪声增加而增加，因而会随着噪声带宽增加而增加。与开环斩波仪表放大器相比，斩波运算放大器更容易受到这种噪声源的影响，因为其输出噪声可以通过反馈网络到达输入端。如果可能，可以使用较高闭环增益来降低噪声带宽。降低噪声带宽的另一种办法是将电容与RG， RS和/或放大器差分输入并联，如图7所示。

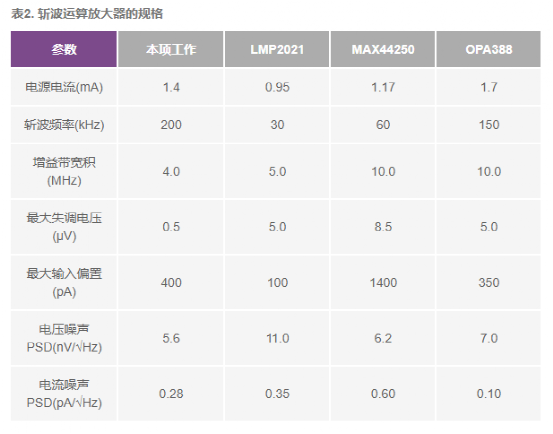
　　VII. 结论 本文确定了另一种输入电流噪声源，它是由输入斩波器处动态电导采样的放大器宽带电压噪声所引起的。本文还发现，与先前告的其他噪声源不同，该电流噪声PSD随着闭环带宽的加宽而增加，原因在于与输入斩波器相关的噪声谱折叠效应。测量结果证实了本文的分析：增益=10时，电流噪声为0.28pA/√Hz；增益=1时，由于闭环带宽增加，电流噪声提高到0.77pA/√Hz。本文为放大器设计人员和用户提供了一些关于降低斩波放大器输入电流噪声的建议。表2比较了本文评估的斩波运算放大器6与其他具有类似电压噪声PSD的新近斩波运算放大器8， 9， 10的整体性能。

责任编辑：xj

原文标题：斩波运算放大器中输入电流噪声和 偶次谐波折叠效应的分析

文章出处：【微信公众号：电子发烧友网】欢迎添加关注！文章转载请注明出处。