图解NumPy的核心概念：向量、矩阵、3维及更高维数组

译者：AI研习社（季一帆）

双语原文链接：NumPy Illustrated： The Visual Guide to NumPy

是一个广泛适用的Python数据处理库，， 等库都基于numpy。同时，在、、等深度许欸小框架中，了解numpy将显著提高数据共享和处理能力，甚至无需过多更改就可以在运行计算。

n维数组是NumPy的核心概念，这样的好处，尽管一维和而为数组的处理方式有些差异，但多数不同维数组的操作是一样的。本文将对以下三个部分展开介绍：

向量——一维数组

矩阵——二维数组

3维及更高维数组

本文受JayAlammar的文章“ A Visual Intro to NumPy”的启发，并对其做了更详细丰富的介绍。

numpy数组 vs. Python列表

乍看上去，NumPy数组与Python列表极其相似。它们都用来装载数据，都能够快速添加或获取元素，插入和移除元素则比较慢。

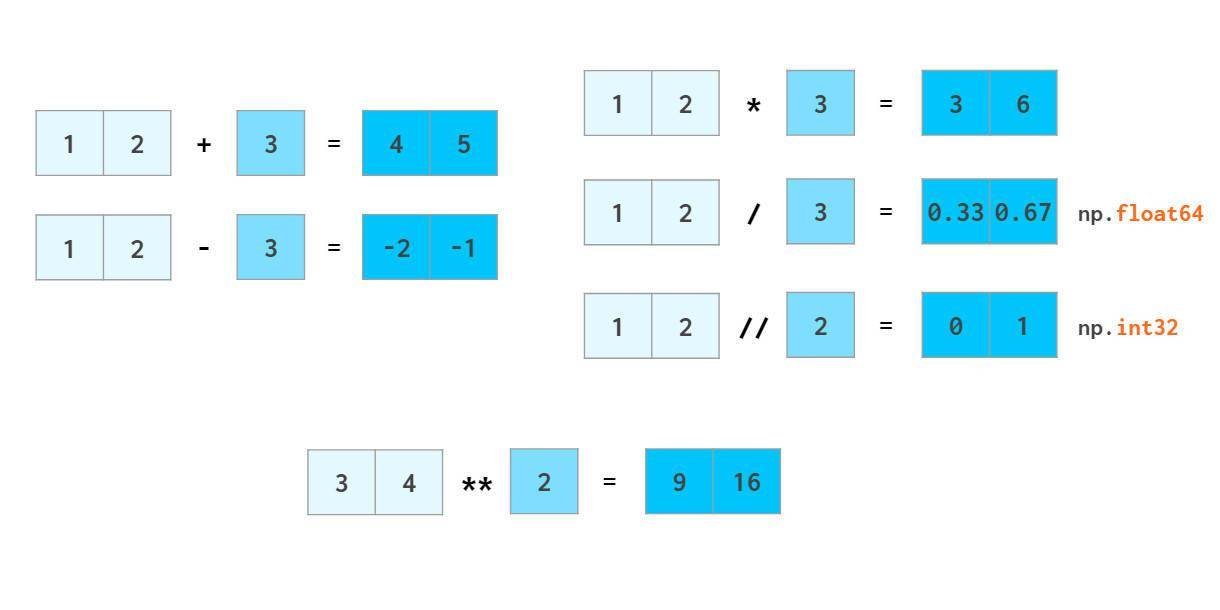
当然相比python列表，numpy数组可以直接进行算术运算：

除此之外，numpy数组还具有以下特点：

更紧凑，高维时尤为明显

向量化后运算速度比列表更快

在末尾添加元素时不如列表高效

元素类型一般比较固定

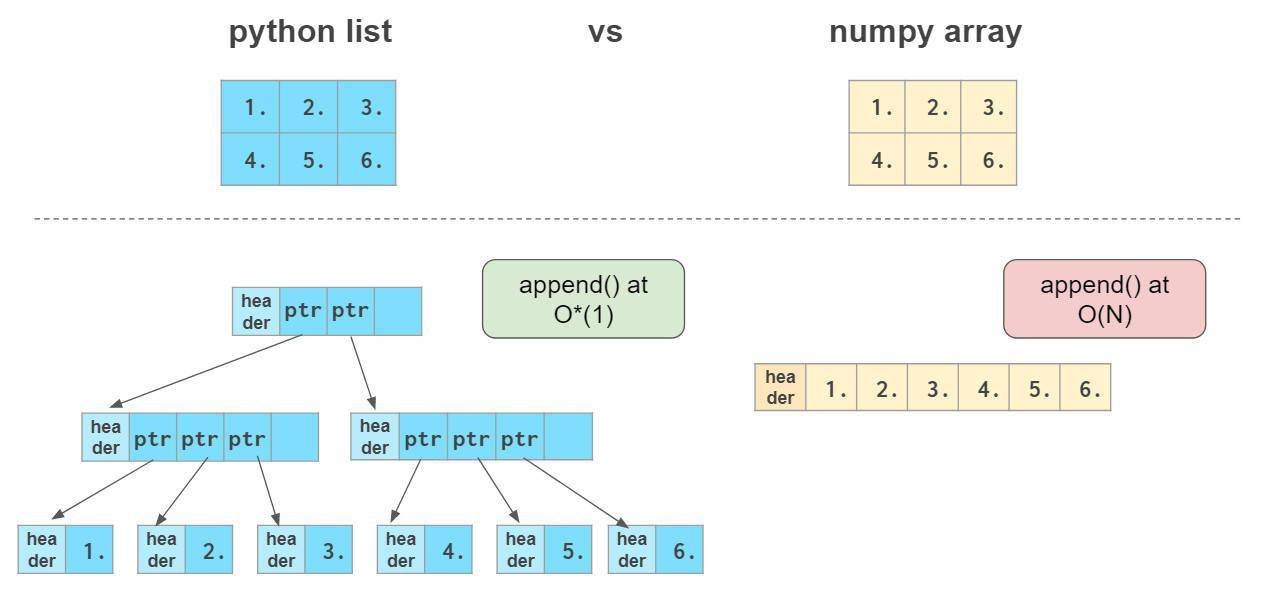
其中，O（N）表示完成操作所需的时间与数组大小成正比（请见），O（1）表示操作时间与数组大小无关（详见）。

1.向量与1维数组向量初始化

通过Python列表可以创建NumPy数组，如下将列表元素转化为一维数组：

注意，确保列表元素类型相同，否则dtype=’object‘，将影响运算甚至产生语法错误。

由于在数组末尾没有预留空间以快速添加新元素，NumPy数组无法像Python列表那样增长，因此，通常的做法是在变长Python列表中准备好数据，然后将其转换为NumPy数组，或是使用np.zeros或np.empty预先分配必要的空间：

通过以下方法可以创建一个与某一变量形状一致的空数组：

不止是空数组，通过上述方法还可以将数组填充为特定值：

在NumPy中，还可以通过单调序列初始化数组：

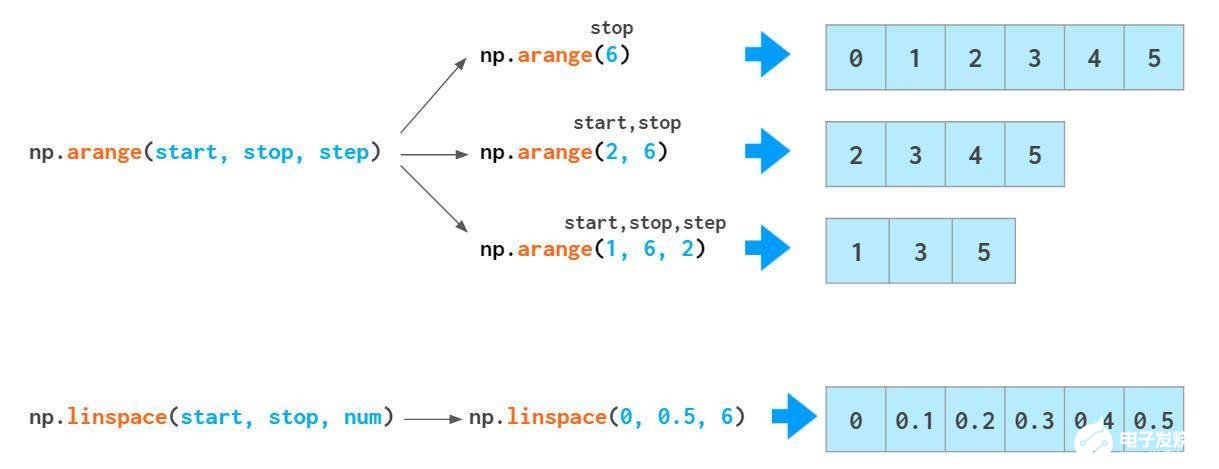
如果您需要［0.， 1.， 2.］这样的浮点数组，可以更改arange输出的类型，即arange（3）.astype（float），但有更好的方法：由于arange函数对类型敏感，因此参数为整数类型，它生成的也是整数类型，如果输入float类型arange（3.），则会生成浮点数。

arange浮点类型数据不是非常友好：

上图中，0.1对我们来说是一个有限的十进制数，但对计算机而言，它是一个二进制无穷小数，必须四舍五入为一个近似值。因此，将小数作为arange的步长可能导致一些错误。可以通过以下两种方式避免如上错误：一是使间隔末尾落入非整数步数，但这会降低可读性和可维护性；二是使用linspace，这样可以避免四舍五入的错误影响，并始终生成要求数量的元素。但使用linspace时尤其需要注意最后一个的数量参数设置，由于它计算点数量，而不是间隔数量，因此上图中数量参数是11，而不是10。

随机数组的生成如下：

向量索引

对于数组数据的访问，numpy提供了便捷的访问方式：

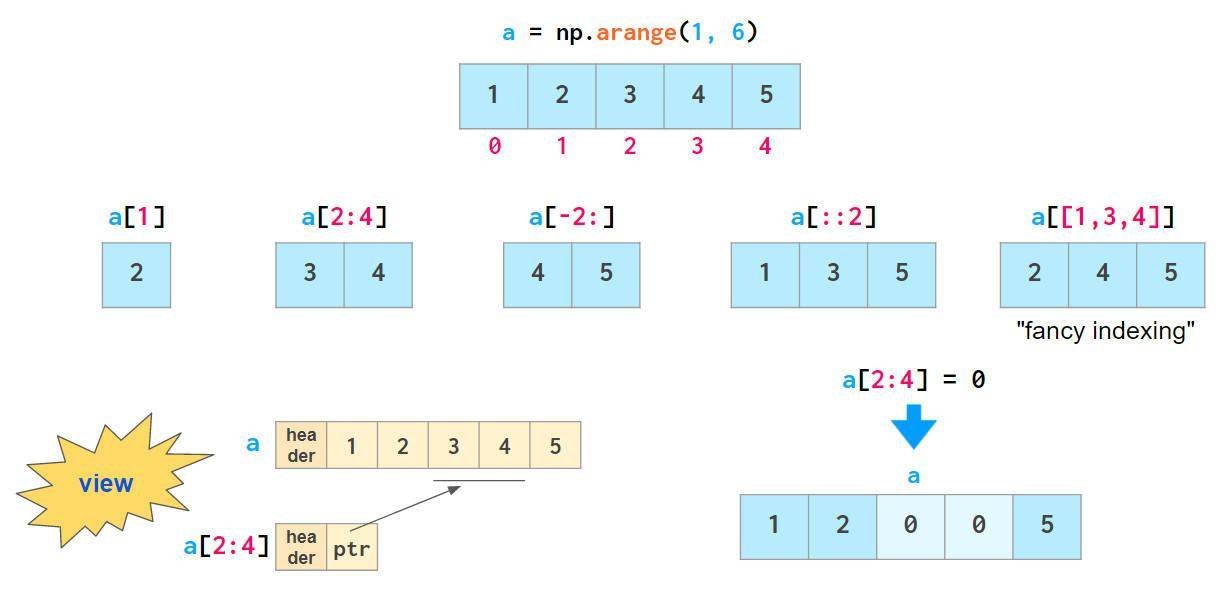
上图中，除“fancy indexing”外，其他所有索引方法本质上都是`views`：它们并不存储数据，如果原数组在被索引后发生更改，则会反映出原始数组中的更改。

上述所有这些方法都可以改变原始数组，即允许通过分配新值改变原数组的内容。这导致无法通过切片来复制数组：

此外，还可以通过布尔索引从NumPy数组中获取数据，这意味着可以使用各种逻辑运算符：

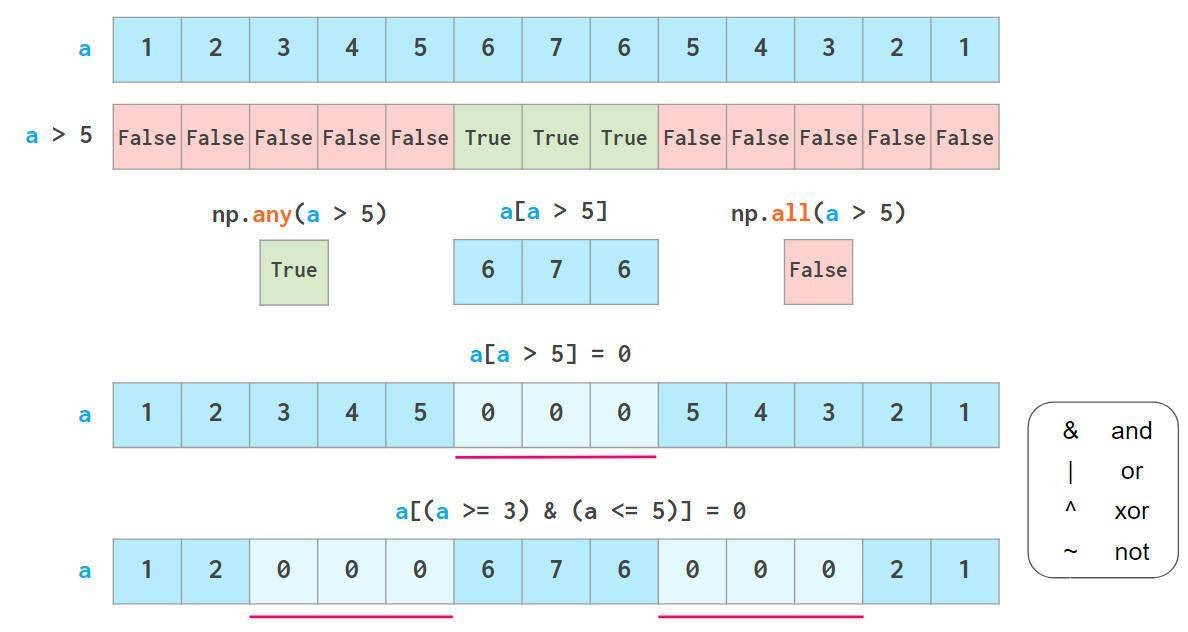
和与其他Python使用类似

注意，不可以使用`3 《= a 《= 5`这样的Python“三元”比较。

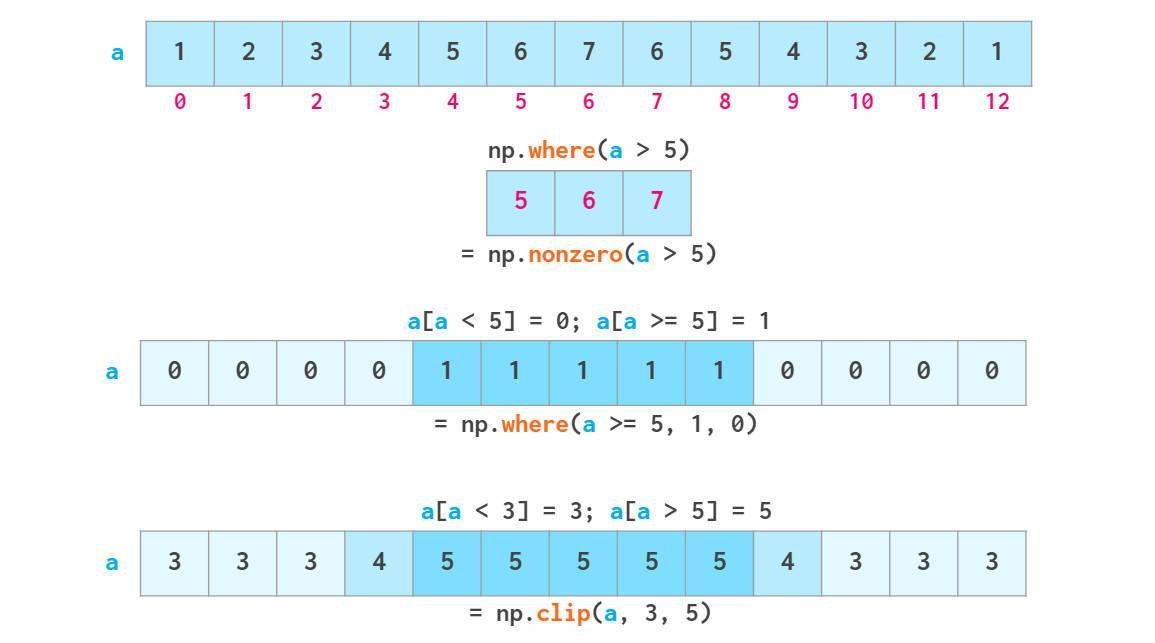
如上所述，布尔索引是可写的。如下图np.where和np.clip两个专有函数。

向量操作

NumPy的计算速度是其亮点之一，其向量运算操作接近C++级别，避免了Python循环耗时较多的问题。NumPy允许像普通数字一样操作整个数组：

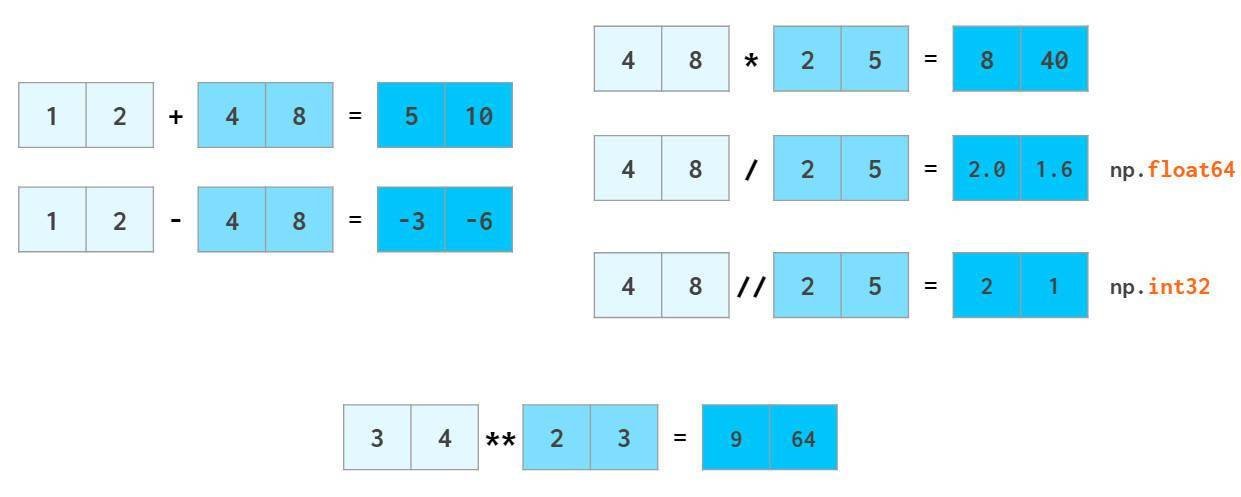
在python中，a//b表示a div b（除法的商），x**n表示 xⁿ

浮点数的计算也是如此，numpy能够将标量广播到数组：

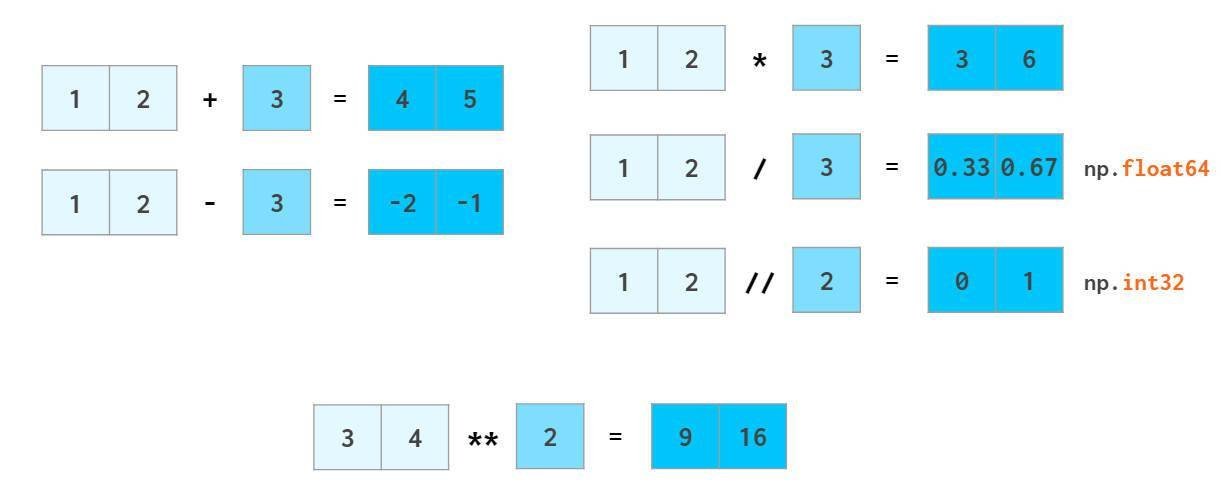
numpy提供了许多数学函数来处理矢量：

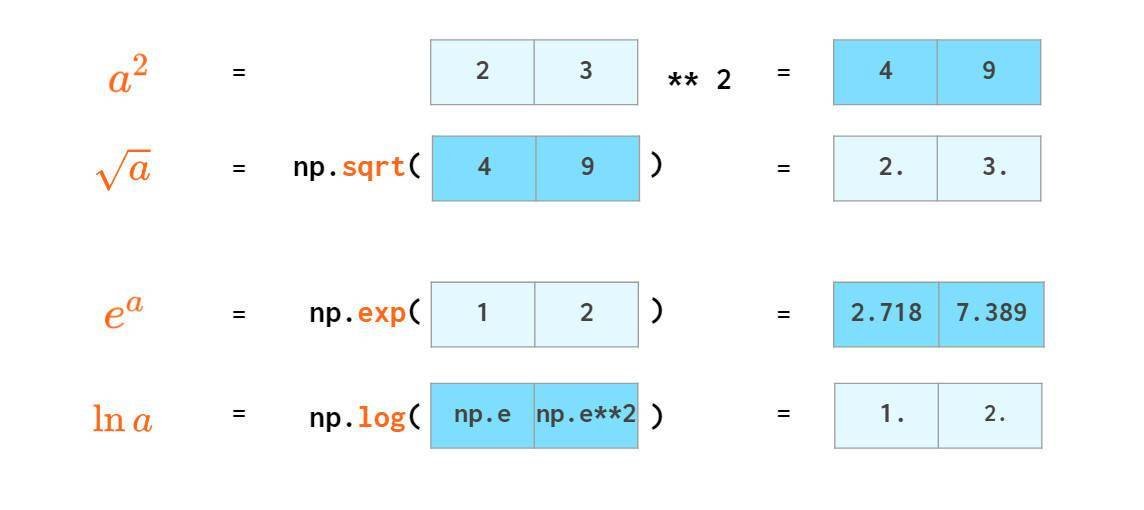
向量点乘（内积）和叉乘（外积、向量积）如下：

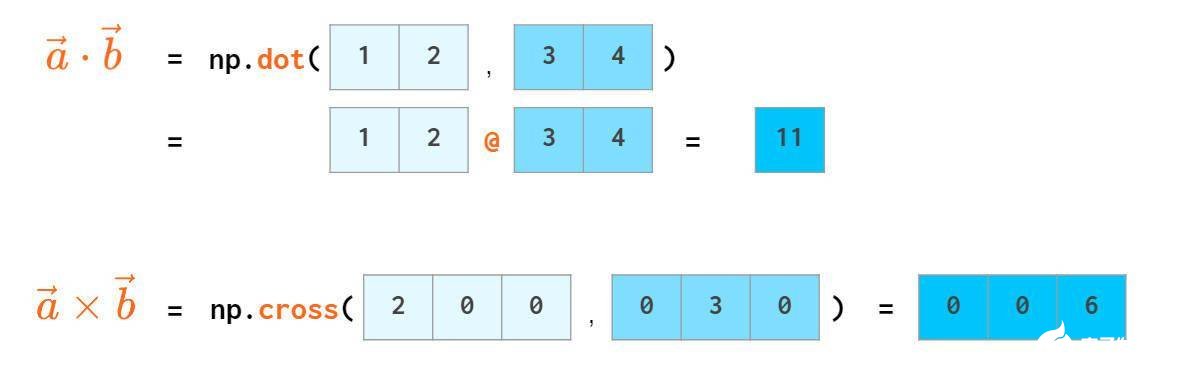
numpy也提供了如下三角函数运算：

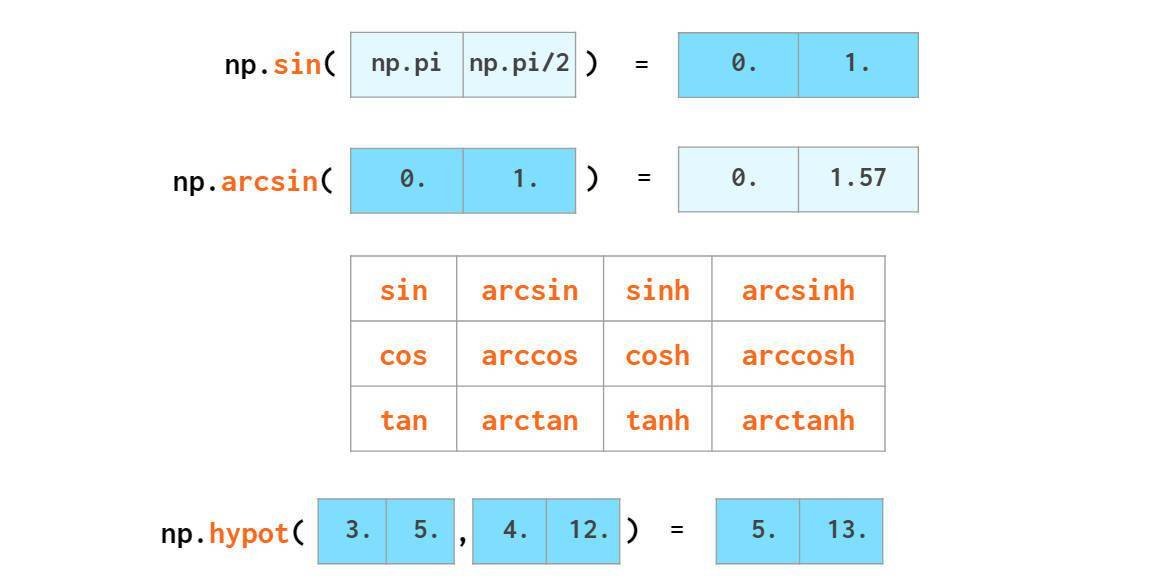
数组整体进行四舍五入：

floor向上取整，ceil向下取整，round四舍五入

np.around与np.round是等效的，这样做只是为了避免 from numpy import *时与Python aroun的冲突（但一般的使用方式是import numpy as np）。当然，你也可以使用a.round。

numpy还可以实现以下功能：

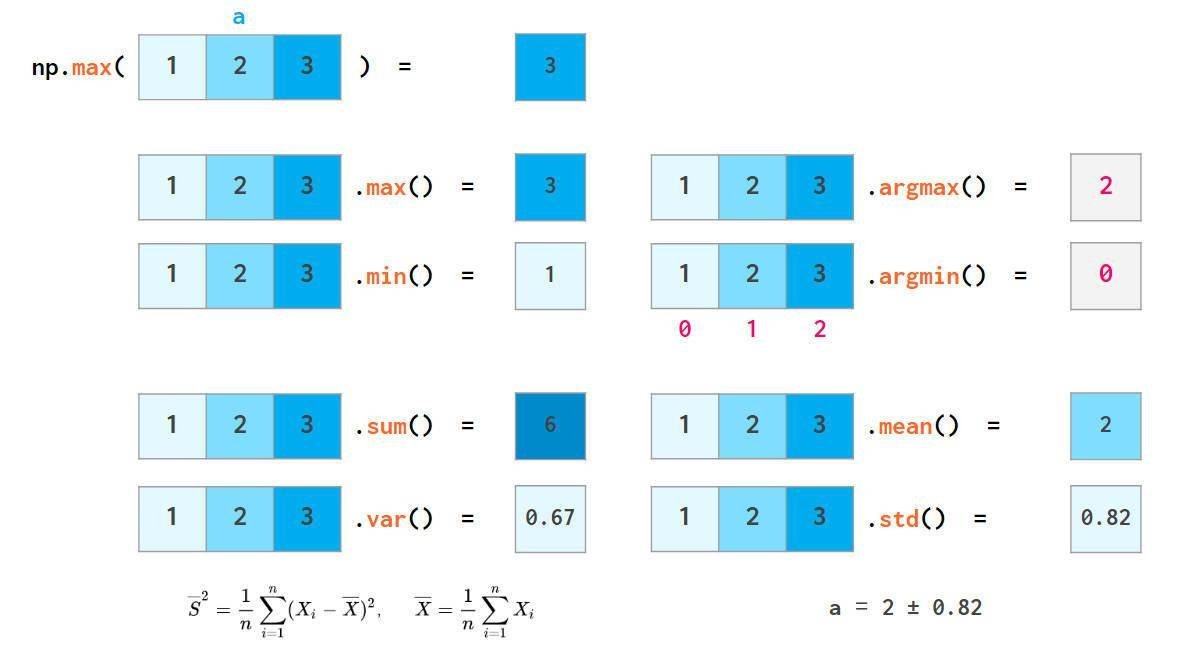
以上功能都存在相应的nan-resistant变体：例如，等

在numpy中，排序函数功能有所阉割：

对于一维数组，可以通过反转结果来解决reversed函数缺失的不足，但在2维数组中该问题变得棘手。

查找向量中的元素

不同于Python列表，NumPy数组没有索引方法。

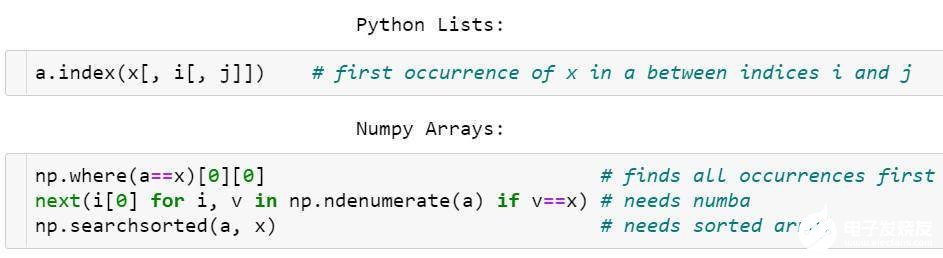
index中的方括号表示j或i&j可以省略

可以通过np.where（a==x）［0］ ［0］查找元素，但这种方法很不pythonic，哪怕需要查找的项在数组开头，该方法也需要遍历整个数组。

使用Numba实现加速查找，next（（i［0］ for i， v in np.ndenumerate（a） if v==x）， -1），在最坏的情况下，它的速度要比where慢。

如果数组是排好序的，使用v = np.（a， x）; return v if a［v］==x else -1时间复杂度为O（log N），但在这之前，排序的时间复杂度为O（N log N）。

实际上，通过C实现加速搜索并不是困难，问题是浮点数据比较。

浮点数比较

np.allclose（a， b）用于容忍误差之内的浮点数比较。

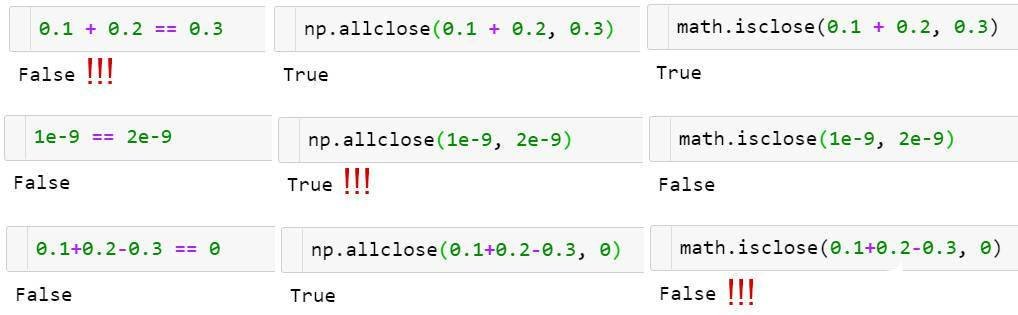
np.allclose假定所有比较数字的尺度为1。如果在纳秒级别上，则需要将默认atol参数除以1e9：np.allclose（1e-9，2e-9， atol=1e-17）==False。

math.isclose不对要比较的数字做任何假设，而是需要用户提供一个合理的abs_tol值（np.allclose默认的atol值1e-8足以满足小数位数为1的浮点数比较，即math.isclose（0.1+0.2–0.3， abs_tol=1e-8）==True。

此外，对于绝队偏差和相对偏差，np.allclose依然存在一些问题。例如，对于某些值a、b， allclose（a，b）！=allclose（b，a），而在math.isclose中则不存在这些问题。查看GitHub上的和相应的了解更多信息。

2.矩阵和二维数组

过去，NumPy中曾有一个专用的matrix类，但现在已被弃用，因此在下文中矩阵和2维数组表示同一含义。

矩阵的初始化语法与向量类似：

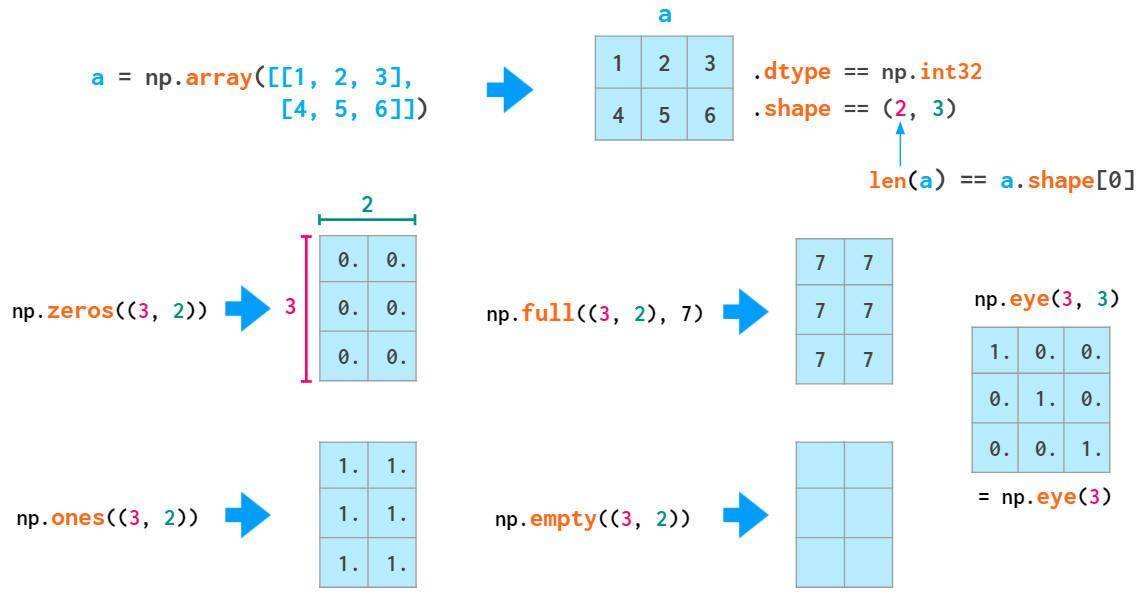
如上要使用双括号，因为第二个位置参数（可选）是为dtype（也接受整数）保留的。

随机矩阵的生成也与向量类似：

二维数组的索引语法要比嵌套列表更方便：

“view”表示数组切片时并未进行任何复制，在修改数组后，相应更改也将反映在切片中。

轴参数

在求和等操作中，NumPy可以实现跨行或跨列的操作。为了适用任意维数的数组，NumPy引入了axis的概念。axis参数的值实际上就是维度数量，如第一个维是axis=0 ，第二维是axis=1，依此类推。因此，在2维数组中，axis=0指列方向，axis=1指行方向。

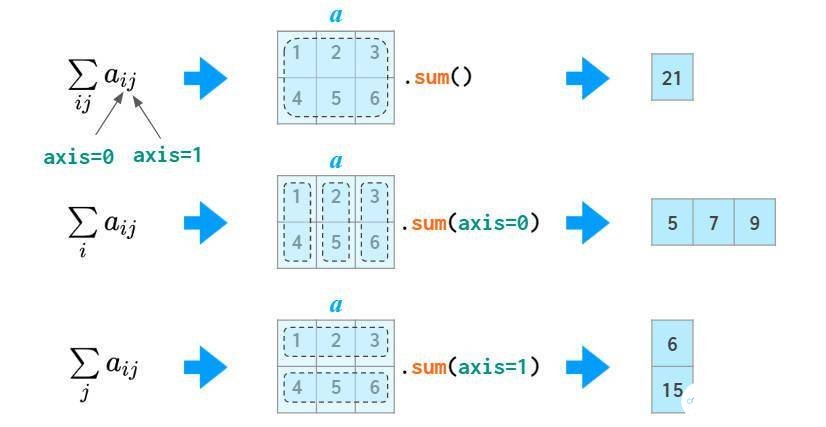
矩阵运算

除了+，-，*，/，//和**等数组元素的运算符外，numpy提供了@运算符计算矩阵乘积：

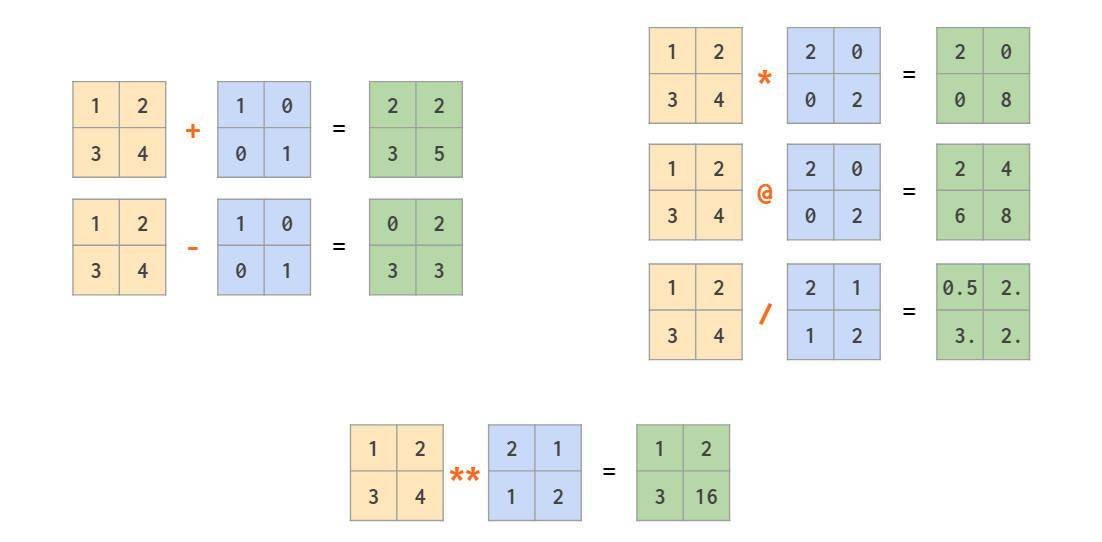
类似前文介绍的标量广播机制，numpy同样可以通过广播机制实现向量与矩阵，或两个向量之间的混合运算：

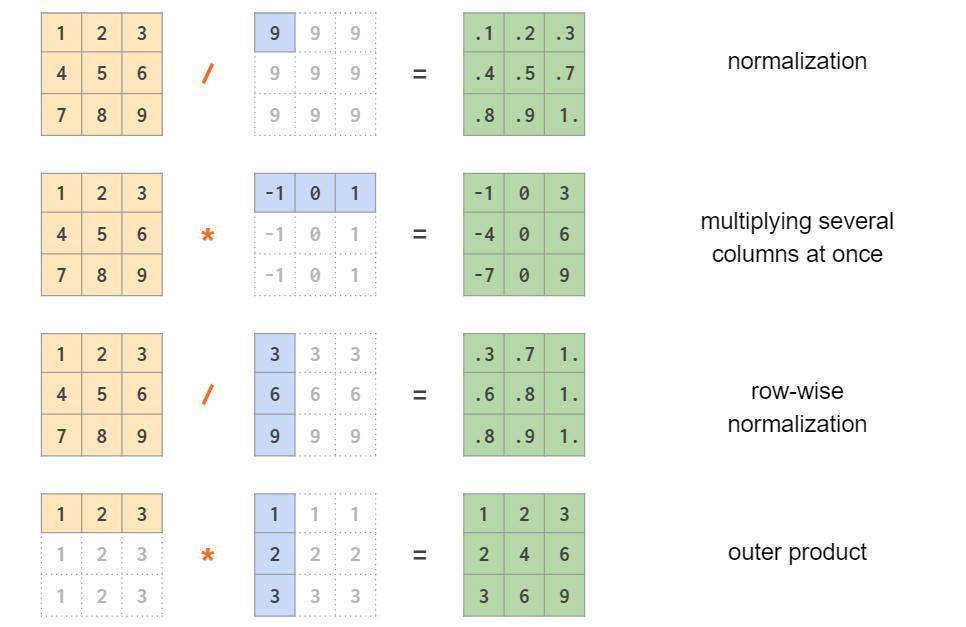
注意，上图最后一个示例是对称的逐元素乘法。使用矩阵乘法@可以计算非对称线性代数外积，两个矩阵互换位置后计算内积：

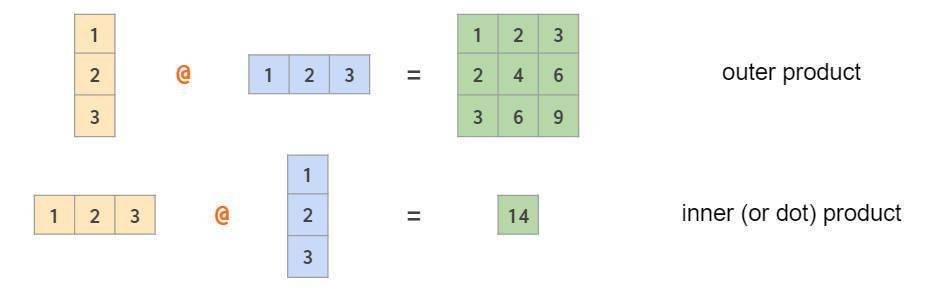
行向量与列向量

根据前文可知，在2维数组中，行向量和列向量被区别对待。通常NumPy会尽可能使用单一类型的1维数组（例如，2维数组a的第j列a［：， j］是1维数组）。默认情况下，一维数组在2维操作中被视为行向量，因此，将矩阵乘行向量时，使用形状（n，）或（1，n）的向量结果一致。有多种方法可以从一维数组中得到列向量，但并不包括transpose：

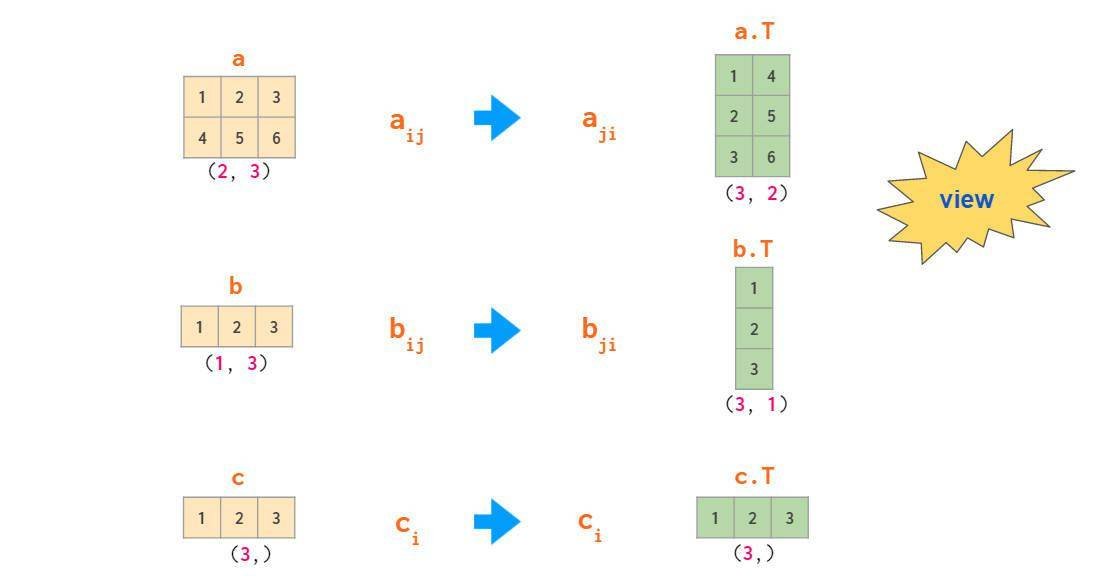
使用newaxis更新数组形状和索引可以将1维数组转化为2维列向量：

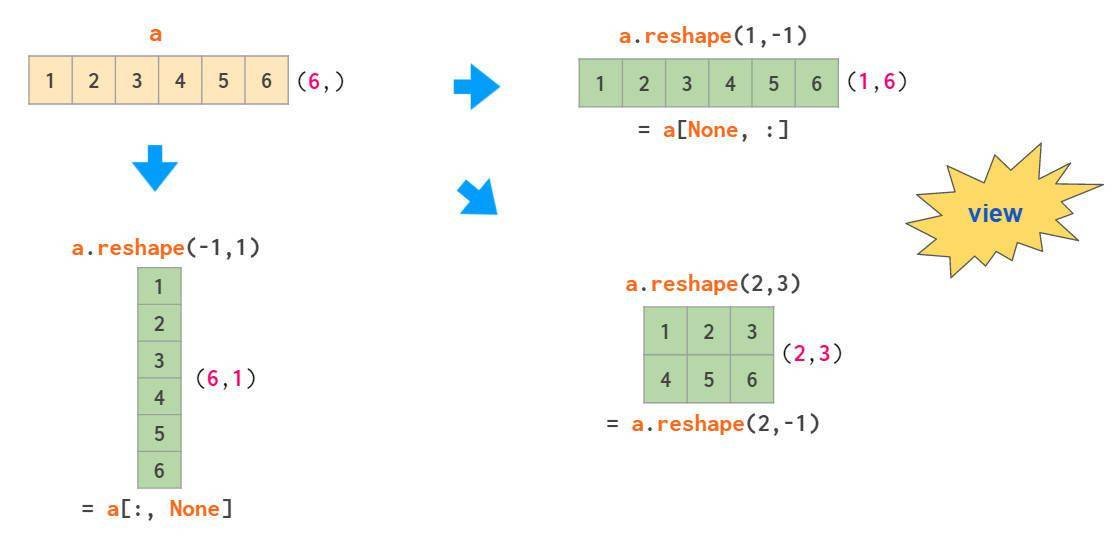
其中，-1表示在reshape是该维度自动决定，方括号中的None等同于np.newaxis，表示在指定位置添加一个空轴。

因此，NumPy中共有三种类型的向量：1维数组，2维行向量和2维列向量。以下是两两类型转换图：

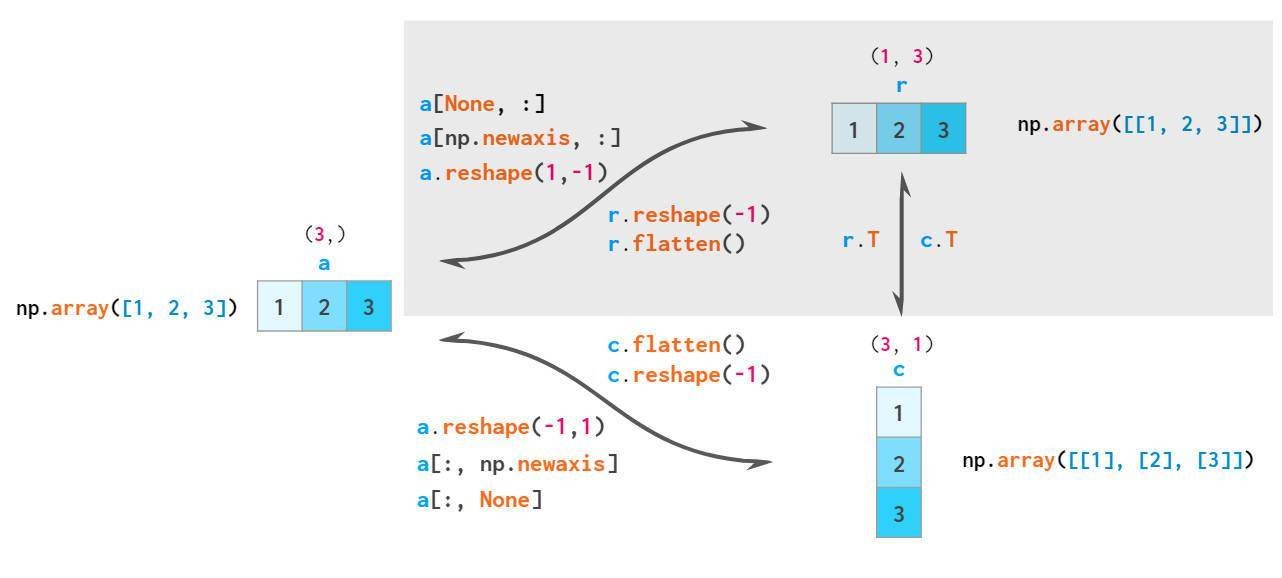
根据广播规则，一维数组被隐式解释为二维行向量，因此通常不必在这两个数组之间进行转换，对应图中阴影化区域。

严格来说，除一维外的所有数组的大小都是一个向量（如a.shape == ［1，1，1，5，1，1］），因此numpy的输入类型是任意的，但上述三种最为常用。可以使用np.reshape将一维矢量转换为这种形式，使用np.squeeze可将其恢复。这两个功能都通过view发挥作用。

矩阵操作

矩阵的拼接有以下两种方式：

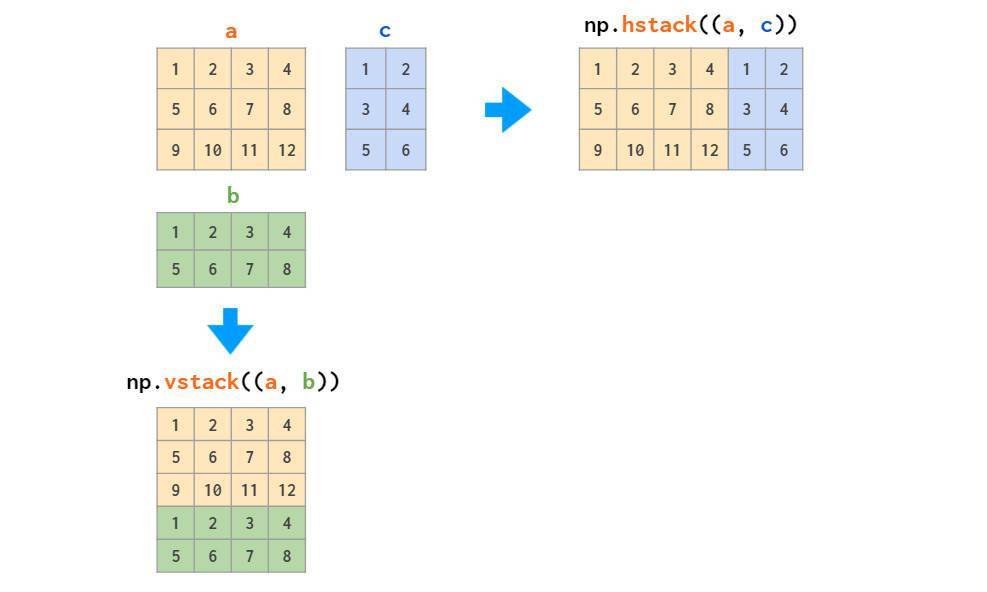
图示操作仅适用于矩阵堆叠或向量堆叠，而一维数组和矩阵的混合堆叠只有通过才可实现，会导致维度不匹配错误。因为前文提到将一维数组作为行向量，而不是列向量。为此，可以将其转换为行向量，或使用专门的函数执行此操作：

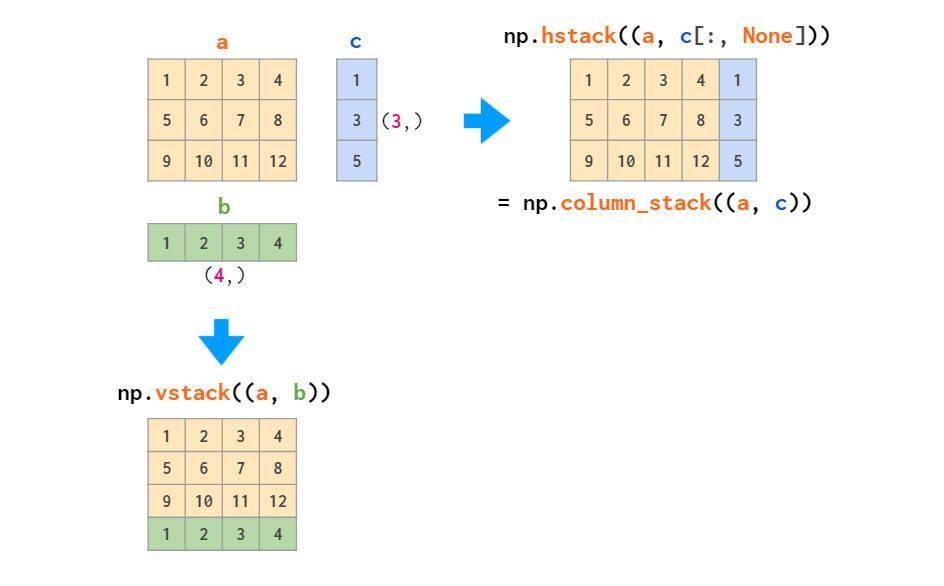
与stack对应的是split：

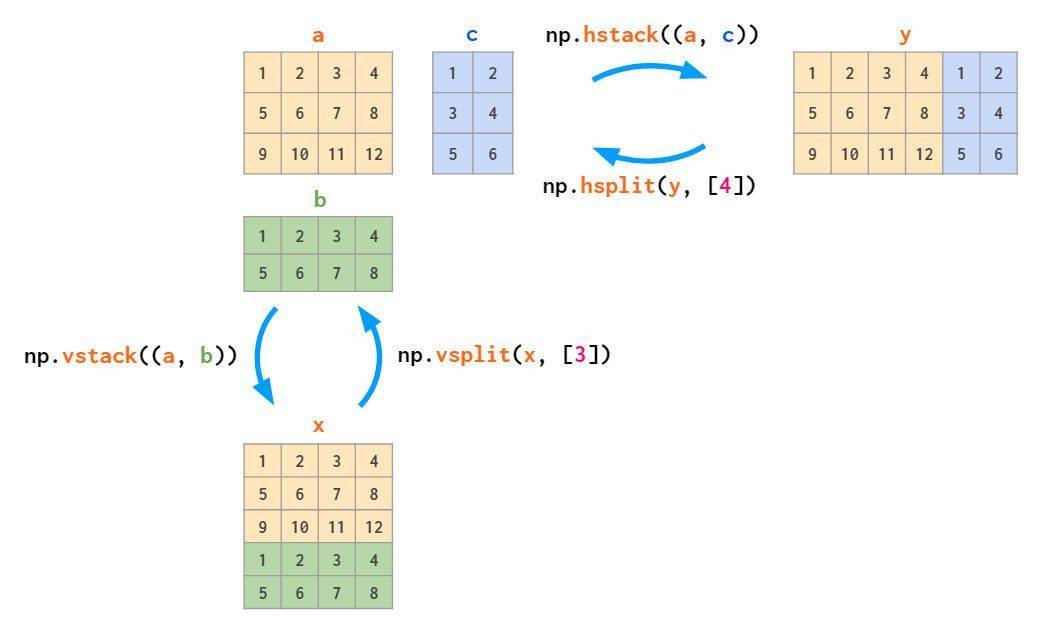
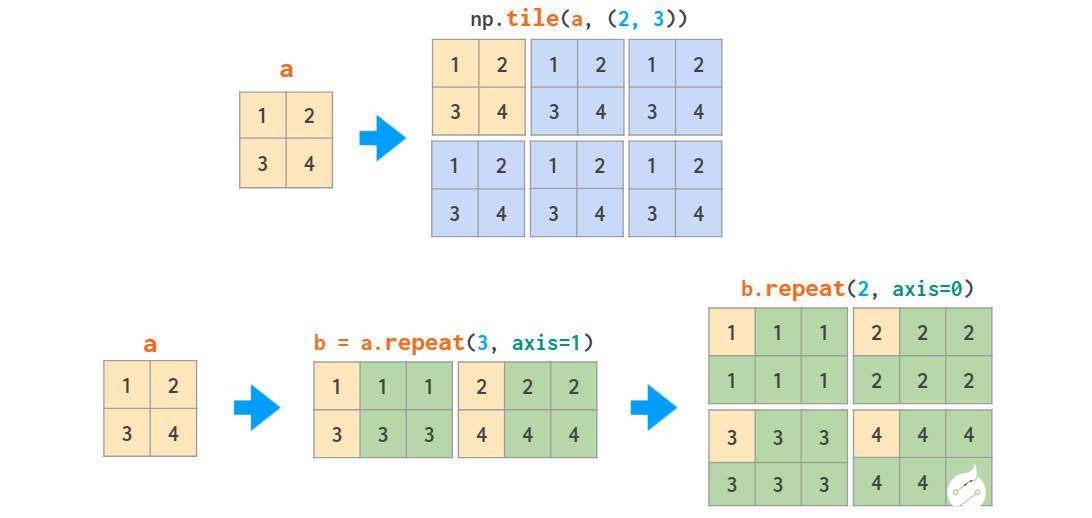
矩阵复制有两种方式：类似粘贴复制；相当于分页打印。

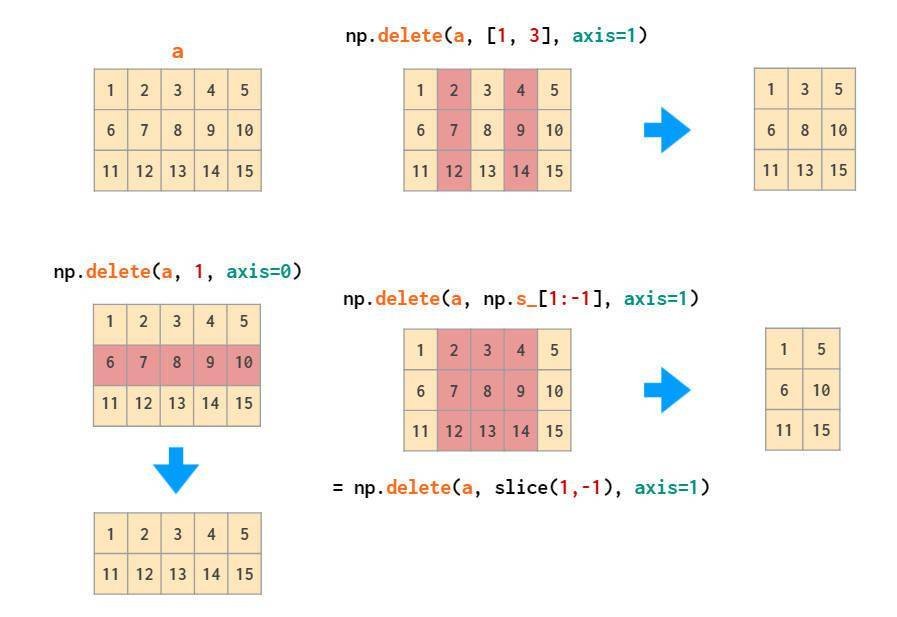
delete可以删除特定的行或列：

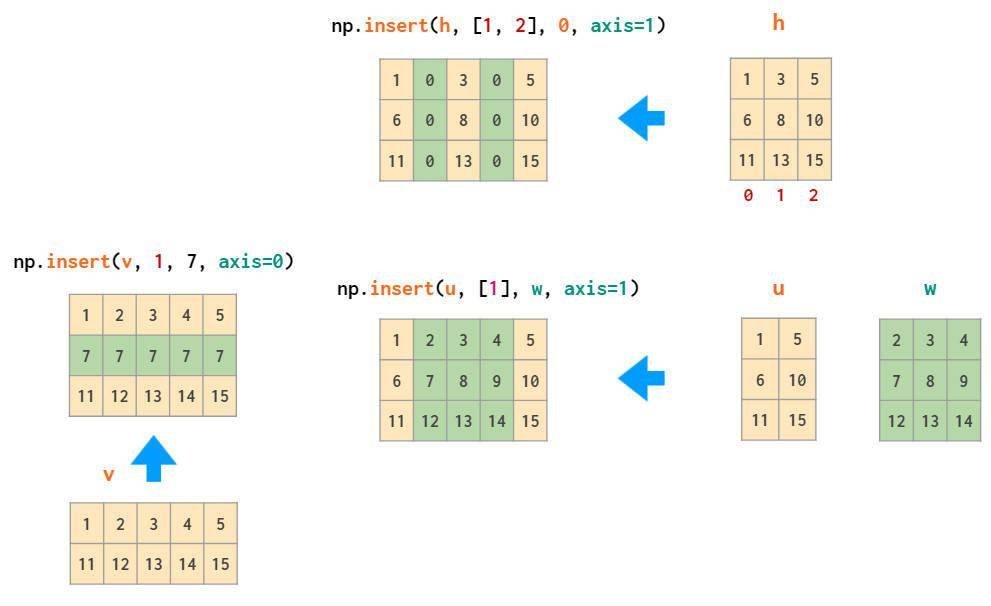
相应插入操作为insert：

与hstack一样，append函数无法自动转置1D数组，因此需要重新调整向量形状或添加维数，或者使用column_stack：

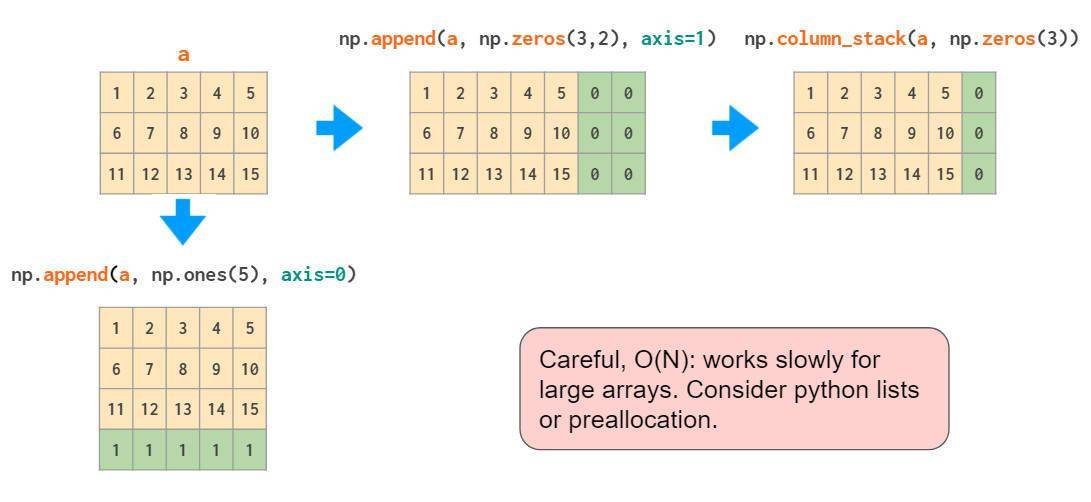
如果仅仅是向数组的边界添加常量值，pad函数是足够的：

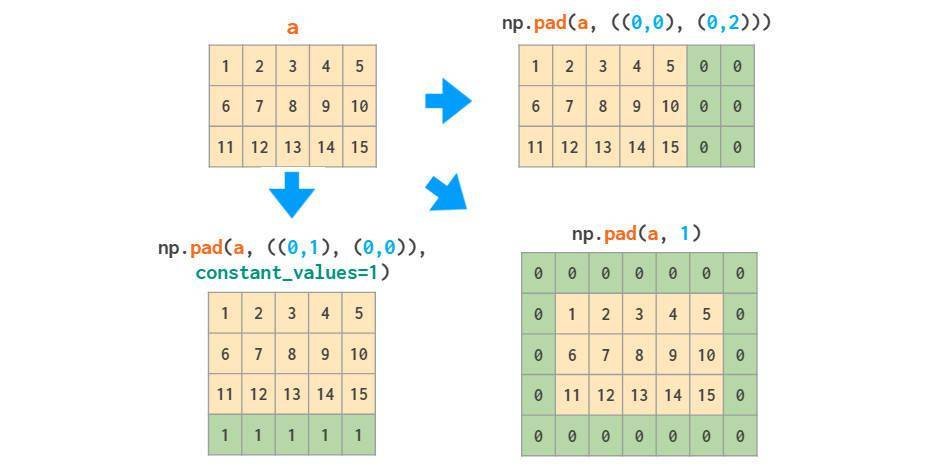
Meshgrids

广播机制使得meshgrids变得容易。例如需要下图所示（但尺寸大得多）的矩阵：

上述两种方法由于使用了循环，因此都比较慢。MATLAB通过构建meshgrid处理这种问题。

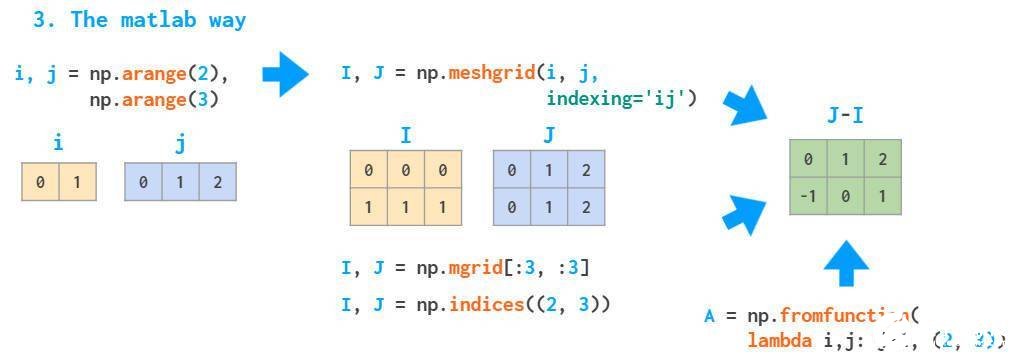
meshgrid函数接受任意一组索引，通过切片和索引生成完整的索引范围，然后，函数根据I和J实现运算。

在NumPy中有一种更好的方法，无需在内存中存储整个I和J矩阵（虽然meshgrid已足够优秀，仅存储对原始向量的引用），仅存储形状矢量，然后通过广播规实现其余内容的处理：

如果没有indexing =’ij‘参数，那么meshgrid将更改参数的顺序，即J，I=np.meshgrid（j，i）——一种用于可视化3D绘图的“xy”模式（祥见该文档）。

除了在二维或三维网格上初始化函数外，网格还可以用于索引数组：

以上方法在稀疏网格中同样适用。

矩阵统计

就像sum函数，numpy提供了矩阵不同轴上的， ， mean/median/percentile， 等函数。

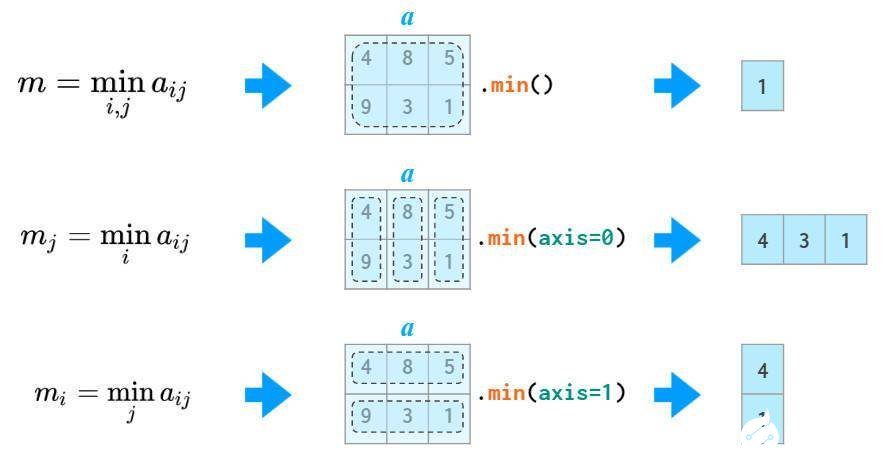
np.amin等同于np.min，这样做同样是为了避免from numpy import *可能的歧义。

2维及更高维中的argmin和argmax函数分别返回最小和最大值的索引，通过unravel_index函数可以将其转换为二维坐标：

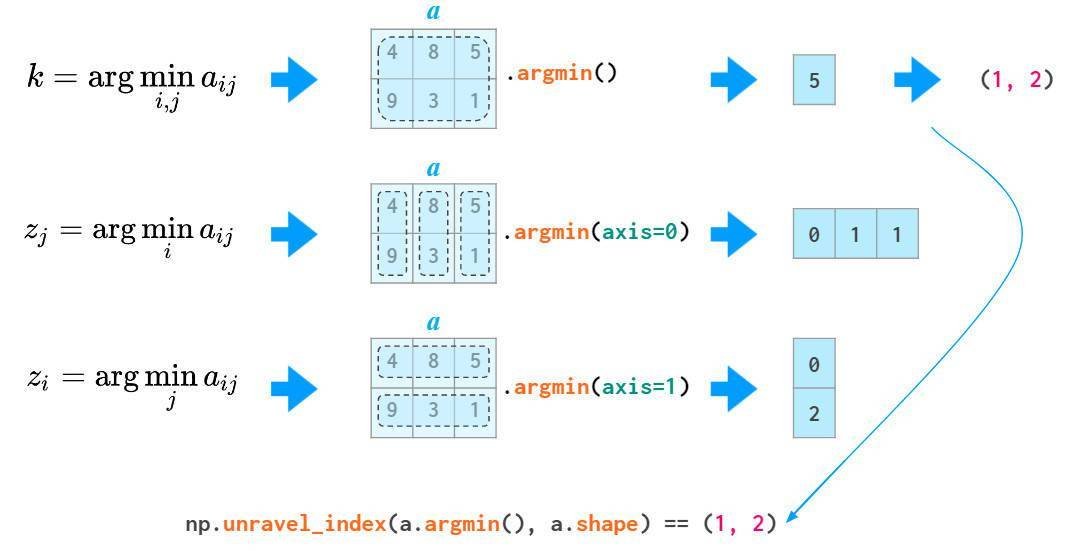
和同样也可作用于特定维度：

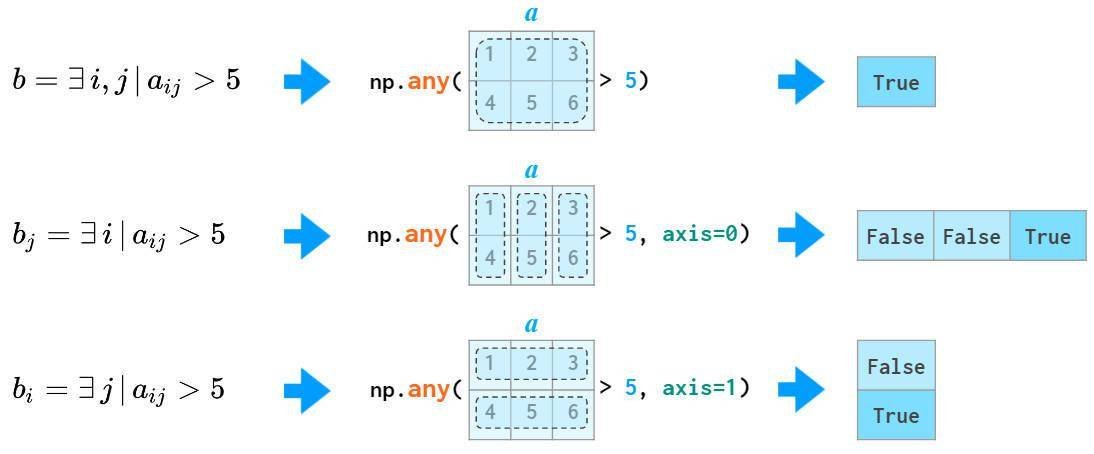
矩阵排序

虽然在前文中，axis参数适用于不同函数，但在二维数组排序中影响较小：

你通常不需要上述这样的排序矩阵，axis不是key参数的替代。但好在NumPy提供了其他功能，这些功能允许按一列或几列进行排序：

1、a［a ［：，0］ .argsort］表示按第一列对数组进行排序：

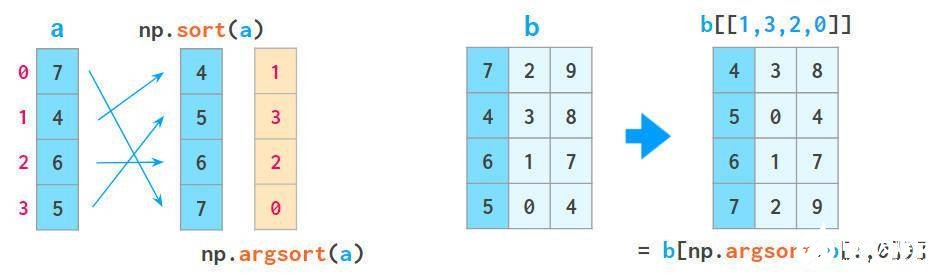
其中，argsort返回排序后的原始数组的索引数组。

可以重复使用该方法，但千万不要搞混：

a = a［a［：，2］.argsort］

a = a［a［：，1］.argsort（kind=’stable‘）］

a = a［a［：，0］.argsort（kind=’stable‘）］

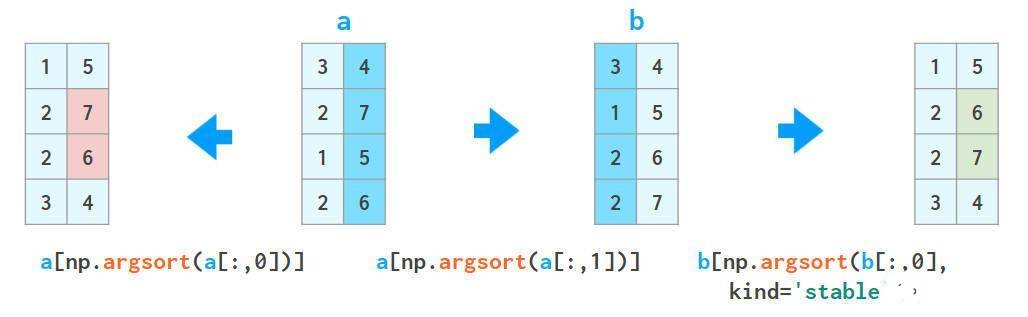
2、函数lexsort可以像上述这样对所有列进行排序，但是它总是按行执行，并且排序的行是颠倒的（即从下到上），其用法如下：

a［np.lexsort（np.flipud（a［2，5］.T））］，首先按第2列排序，然后按第5列排序；a［np.lexsort（np.flipud（a.T））］，从左到右依次排序各列。

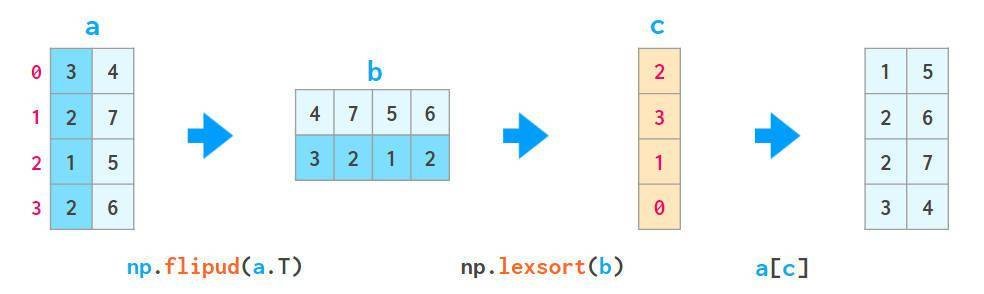
其中，沿上下方向翻转矩阵（沿axis = 0方向，与a ［：：-1，。。.］等效，其中。。.表示“其他所有维度”），注意区分它与，fliplr用于1维数组。

3、sort函数还有一个order参数，但该方法极不友好，不推荐学习。

4、在pandas中排序也是不错的选择，因为在pandas中操作位置确定，可读性好且不易出错：

- pd.DataFrame（a）.sort_values（by=［2，5］）.to_numpy，先按第2列排序，再按第5列排序。

-pd.DataFrame（a）.sort_values.to_numpy，按从左到右的顺序对所有列进行排序。

3、3维及更高维数组

通过重塑1维向量或转换嵌套Python列表来创建3维数组时，索引分别对应（z，y，x）。索引z是平面编号，（y，x）坐标在该平面上移动：

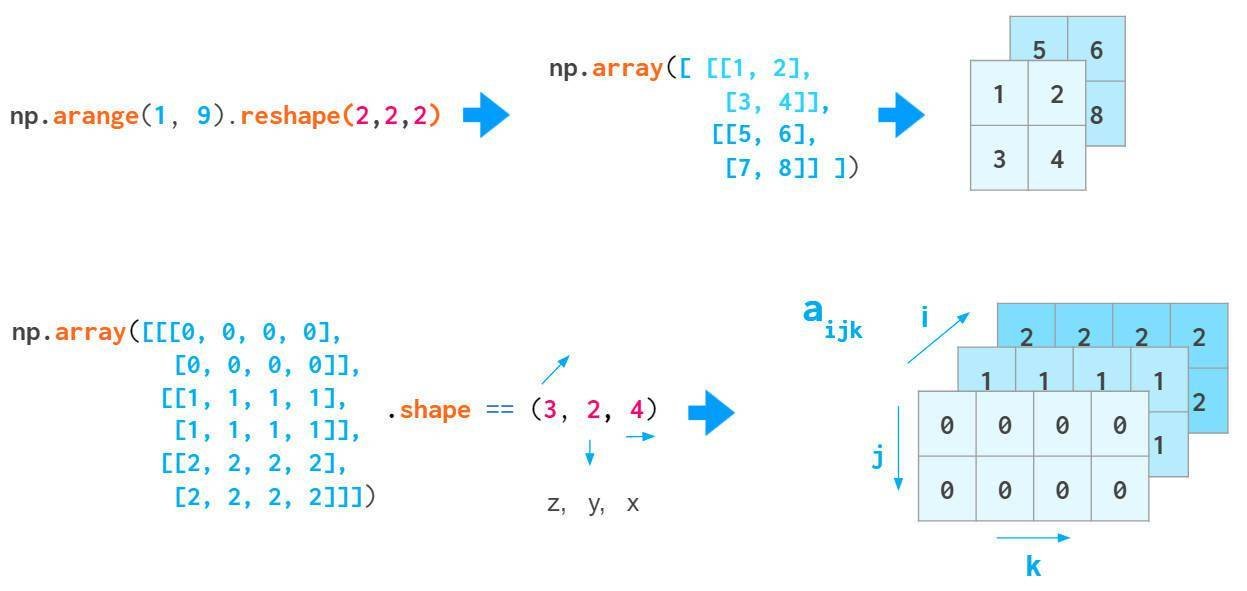
通过上述索引顺序，可以方便的保留灰度图像，a［i］表示第i个图像。

但这样的索引顺序并不具有广泛性，例如在处理RGB图像时，通常使用（y，x，z）顺序：首先是两个像素坐标，然后才是颜色坐标（中的RGB，中的BGR）：

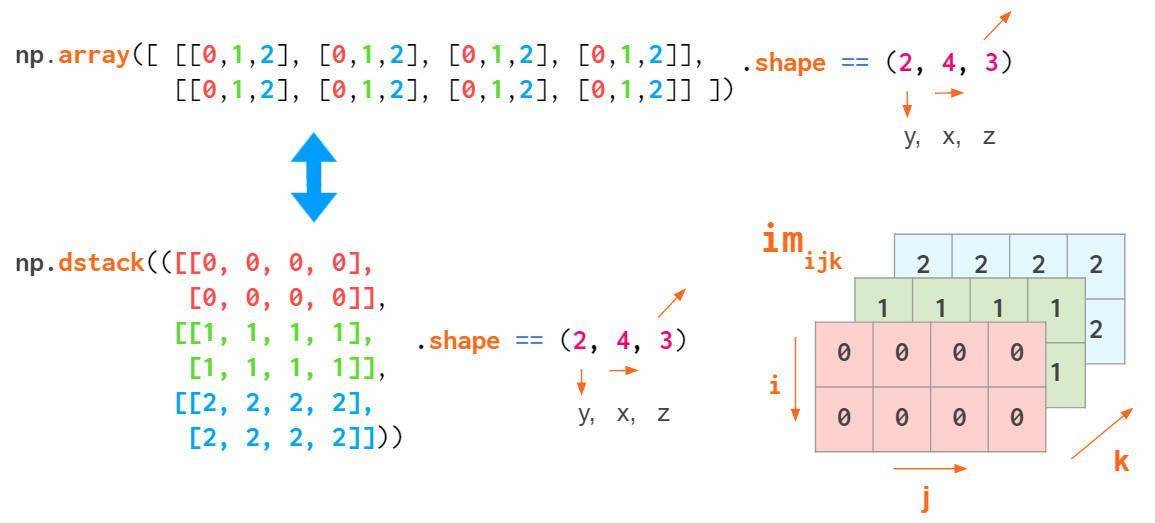
这样可以方便地定位特定像素，如a［i，j］给出像素（i，j）的RGB元组。

因此，几何形状的创建实际取决于你对域的约定：

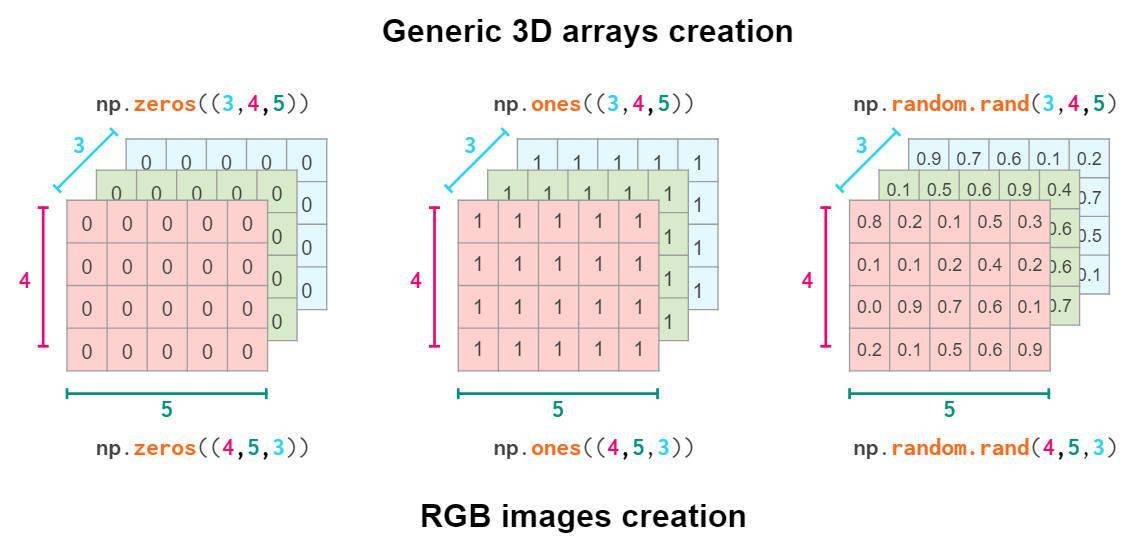
显然，hstack，vstack或dstack之类的NumPy函数并不一定满足这些约定，其默认的索引顺序是（y，x，z），RGB图像顺序如下：

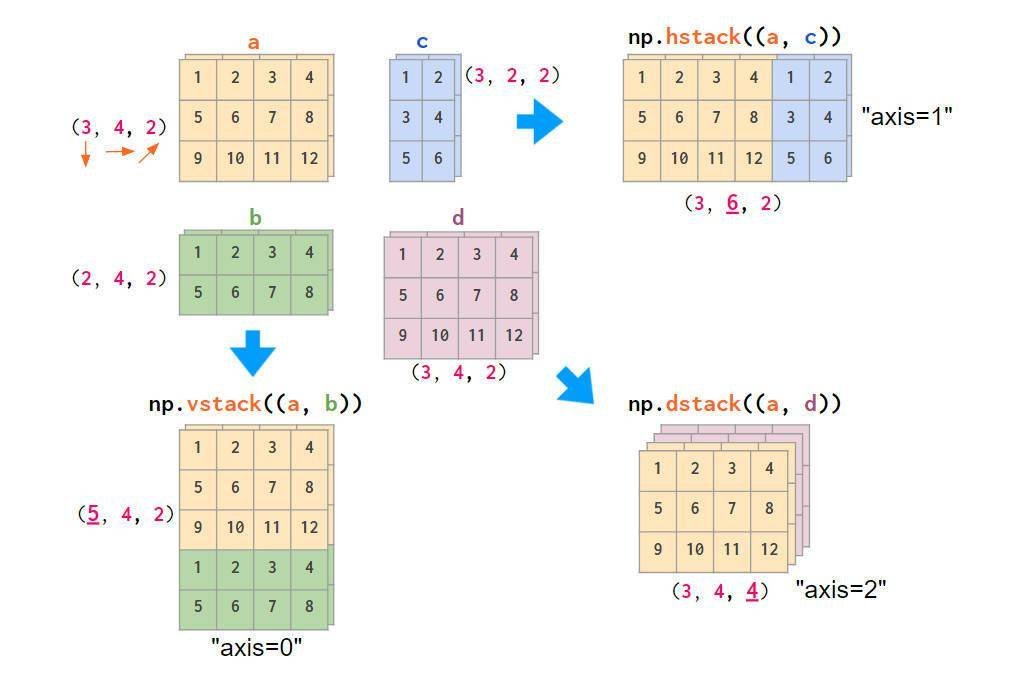
如果数据不是这样的布局，使用concatenate命令可以方便的堆叠图像，并通过axis参数提供索引号：

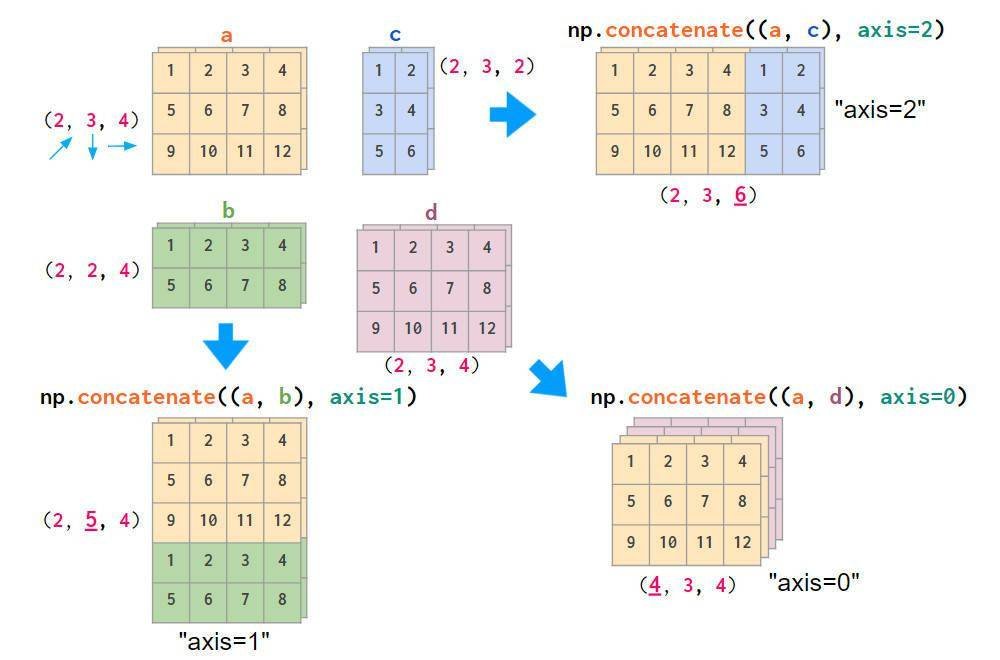
如果不考虑轴数，可以将数组转换hstack和相应形式：

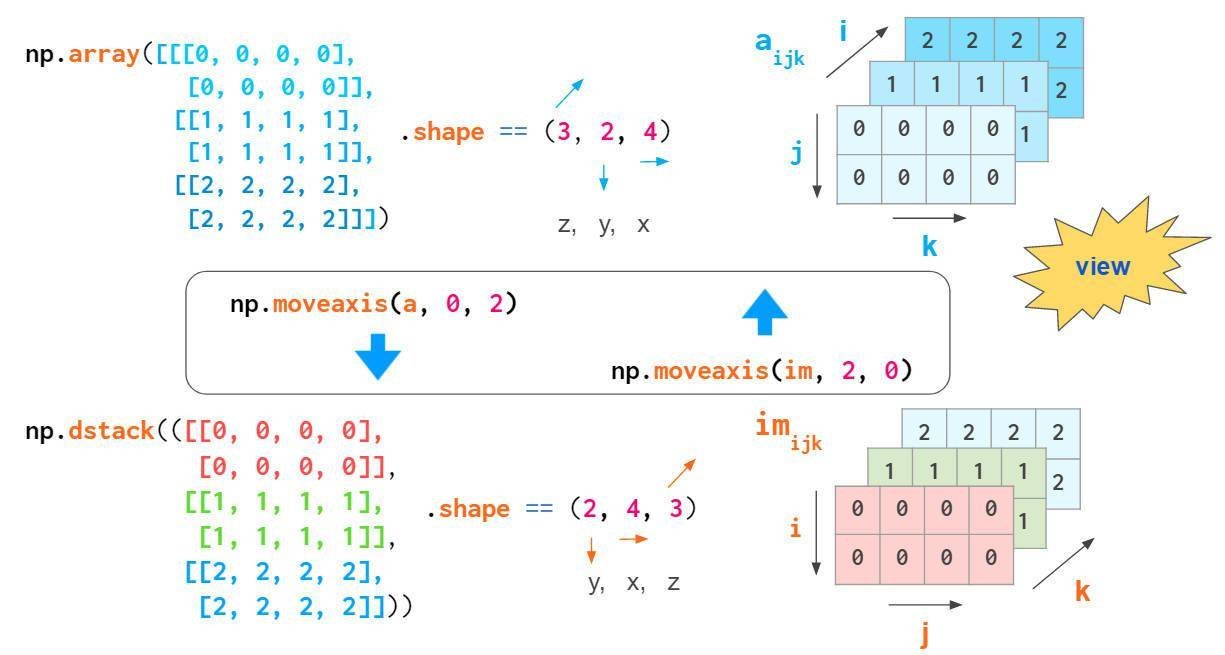
这种转换非常方便，该过程只是混合索引的顺序重排，并没有实际的复制操作。

通过混合索引顺序可实现数组转置，掌握该方法将加深你对3维数据的了解。根据确定的轴顺序，转置数组平面的命令有所不同：对于通用数组，交换索引1和2，对于RGB图像交换0和1：

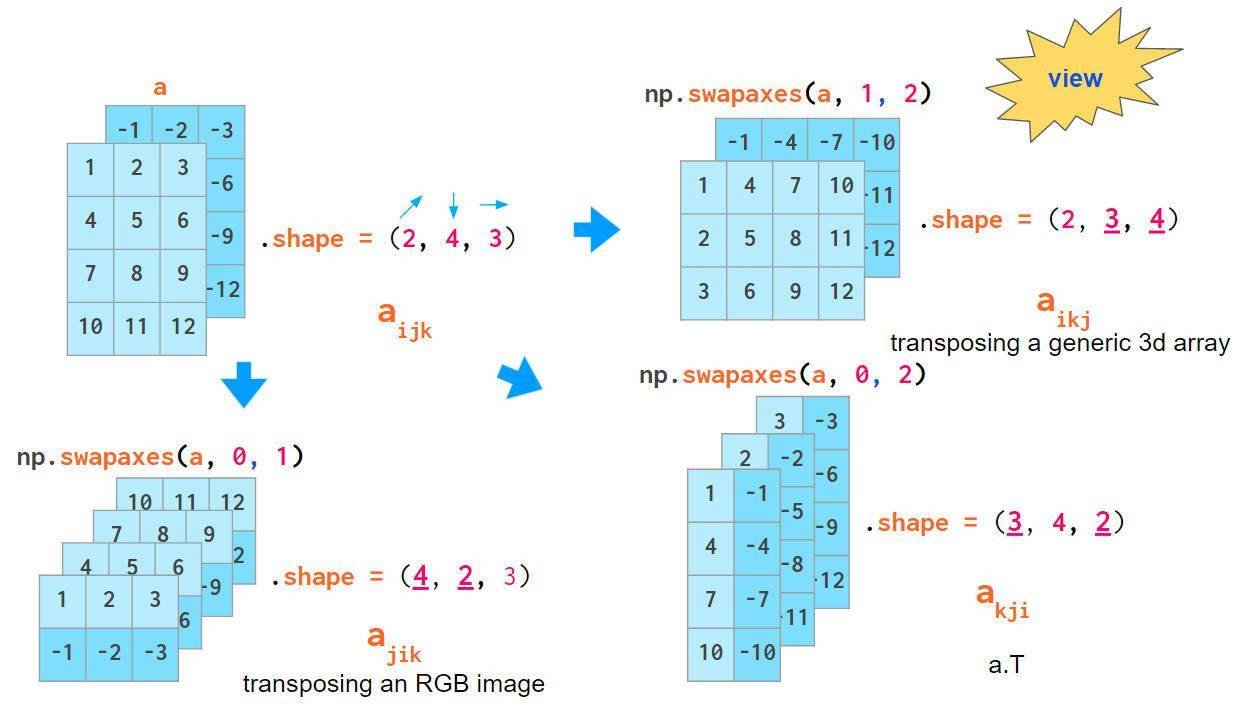
注意，（a.T）的默认轴参数会颠倒索引顺序，这不同于上述述两种索引顺序。

广播机制同样适用多维数组，更多详细信息可参阅笔记“ ”。

最后介绍（Einstein summation）函数，这将使你在处理多维数组时避免很多Python循环，代码更为简洁：

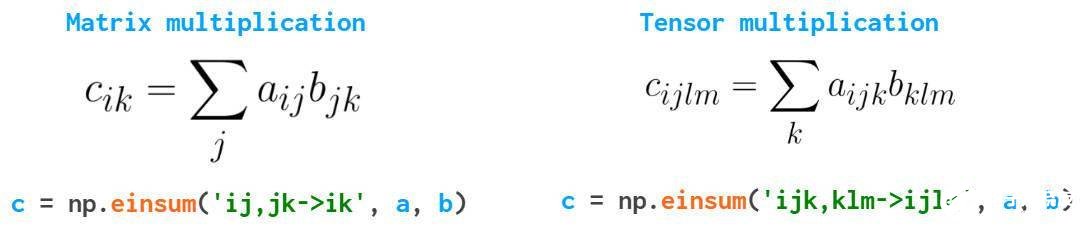
该函数对重复索引的数组求和。在一般情况下，使用np.tensordot（a，b，axis=1）就可以，但在更复杂的情况下，einsum速度更快，读写更容易。

如果你想看看自己的NumPy水平到底如何，可以在GitHub上进行练习——例如。

对于本文未介绍到的NumPy常用功能，欢迎各位读者通过、给我留言，我将进一步完善本文！