

存在互感的电感串并联的详细资料说明
电子说
描述
以电感为中心的RLC串联电路
电感器是电路中常见的重要元器件,常用在信号滤波、电能转换、信号耦合以及磁场检测等。它利用电磁感应原理对流过的电流的变化产生感应电动势,两端的电压与电流的变化率成正比,其中的比率就是电感的重要参数:电感量,通常记作L。
▌简单电感的串并联
与电阻、电容以上,电感也可以通过串联、并联形成新的电感。计算串联、并联电感的值与电阻的串并联的计算公式基本一致。多个电感串联的电感量等于各个电感的电感值相加;多个电感并联的电感量等于各并联电感的电感的的倒数之和再取倒数。
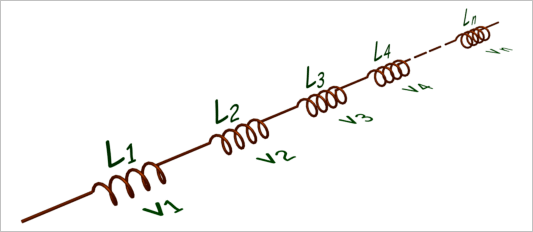
▲ 电感串联
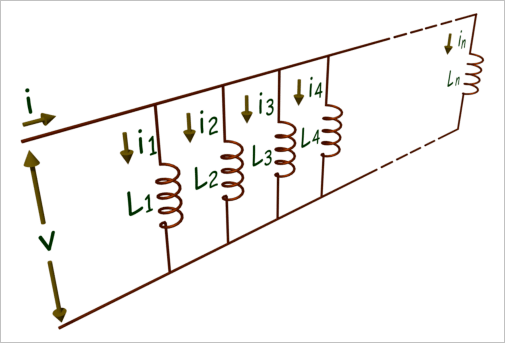
▲ 电感并联
与电阻不同的是,电感之间有可能会出现相互的电磁耦合的关系,特别是对于空心电感,磁场会存在电感周围很大的空间内。如果两个电感之间的距离很近,方向又一致,就很容易电磁耦合,度量两个线圈之间电磁耦合程度通常使用互感(Mutual Inductance)来度量,它表征了一个线圈中的电流变化在另外一个线圈中所产生感应电动势的大小。
对于有互感的M两个线圈L1,L2,可以列写出它们之间的等效电路:
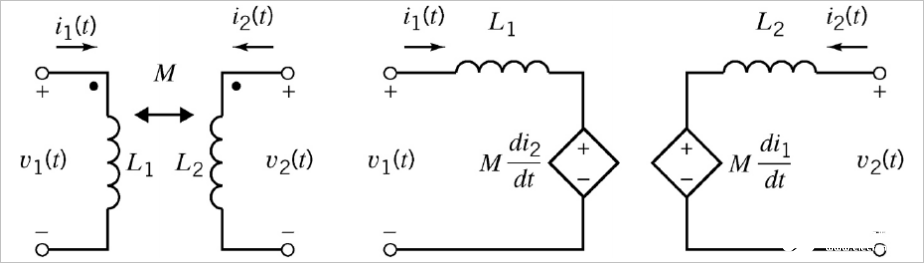
▲ 两个有互感的线圈等效电路
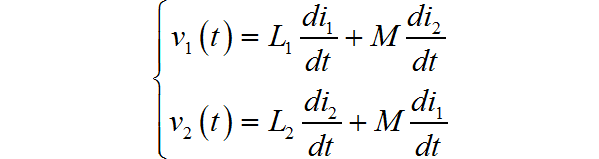
根据产生感应电动势的极性,可以定义出两个互感线圈之间的“ 同铭端”,根据极性与参考电压方向是否相同,可以分为同相互感和反相互感。
对于之间有互感的电感的串联、并联之后电感的计算就变得复杂了。在网络文章 Mutually coupled inductors. Coupling coefficient. Power and energyof mutually coupled inductors. Analysis of circuits with mutuallycoupled inductor.[1] 中,给出了互感线圈的串、并联计算基本方法。
▌有互感电感的串联
两个线圈 之间存在着互感 ,当它们同相串联的时候,对应的电感量为:
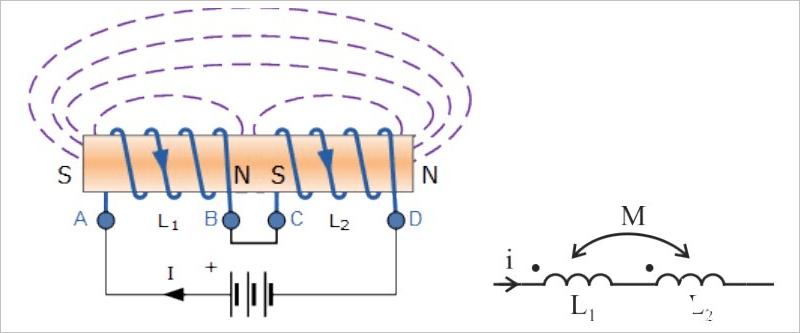
▲ 两个电感同相串联
可以可跟KVL定理,列写出串联支路电压方程,可以证明该公式:
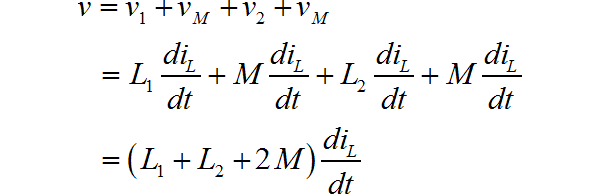
如果是反相串联的时候,按照相同的方式,可以证明对应的等效电感量为:
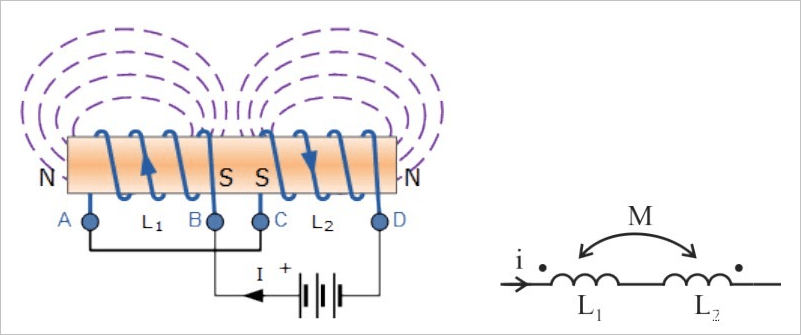
▲ 两个电感线圈反相串联
根据这个公式,可以来测量两个线圈之间的互感量M。也就是通过分别测量L1,L2,然后在分别测量他们同相和反相串联后的电感,便可以计算出它们之间的互感M。
▌有互感电感并联
当两个有互感M的线圈L1,L2并联时,对应的等效电感分别为:
(1) 同相并联
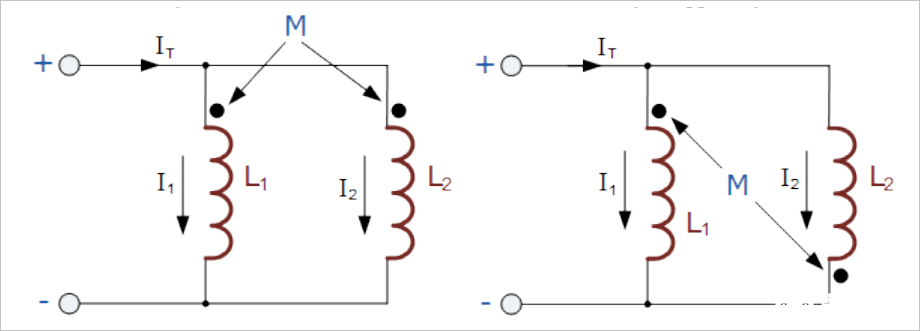
▲ 带有互感的线圈并联
左:同相并联;右:反相并联 (2) 反相并联
公式的证明过程稍微复杂,可以参见前面 论文中的求解过程。[1]
从上面公式可以看到,当互感量M等于0时,它们就退化成最初的简单电感的串并联计算公式了。
▌互感线圈等效变换
存在互感电路往往会使得电路分析变得复杂。将两个互感的线圈使用T型电路进行等效变换可以简化电路分析。下面给出了通过互感耦合在一起的电路等效变换。
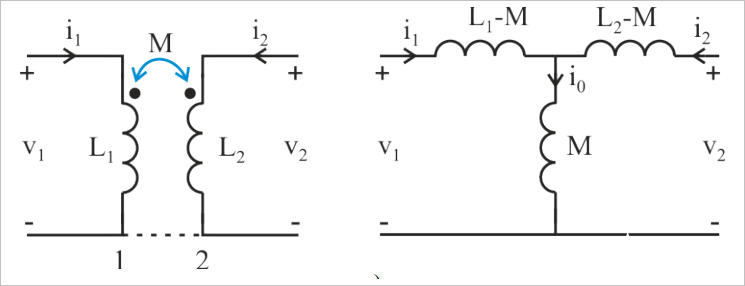
▲ 同相互感等效变换
等效转换后的电路消除了互感,之后的电路分析可以使用基尔霍夫电压、电流定理(KCL&KVL)进行分析。
-
互感电感的串并联计算方法2023-03-03 33937
-
怎样去计算有互感电感串并联的等效电感2021-08-31 10319
-
互感器详细资料2009-12-11 4243
-
CAD电气制图的详细资料说明2019-02-18 1640
-
ADC和DAC的设计经验详细资料说明2019-03-12 1880
-
电力电子教程之电感的详细资料说明2019-04-25 1171
-
电机驱动的详细资料说明2019-05-06 1597
-
使用LabVIEW设计扫雷游戏的详细资料说明2019-05-21 2728
-
电工口诀的详细资料说明2019-12-12 1976
-
AD快捷键的详细资料说明2020-03-17 1570
-
数字信号处理的详细的详细资料说明2020-03-04 1073
-
电网距离保护的详细资料说明2020-04-10 1057
-
LabVIEW的程序实例详细资料说明2021-02-05 2181
-
Bluetooth蓝牙的详细资料说明2021-02-26 3535
-
LED灯串并联电阻的选择2023-05-01 8518
全部0条评论

快来发表一下你的评论吧 !

