新型倍流整流电路拓扑在通信电源中的应用研究

倍流整流电路首先是由A．Cook在1924年出版的《E1ements of Electrical Engineering》书中加以描述，并于20世纪30年代在电子管电路中得到使用。1987年7月Ole S．Seiersen首次在丹麦申请专利，并在1991年FIFPC会议上发表相关的学术论文。

本文分析了一种新型的倍流整流电路拓扑，如果在通信电源中得到应用，可以提高大电流输出时副边整流电路的效率。

1 全波整流和倍流整流

传统上，通信电源变压器副边整流电路大多采用图1（a）所示带中心抽头的全波整流电路，该电路拓扑结构简单．器件总数少，二极管通态损耗小，但是变压器副边绕组的利用率较低。随着开关电源技术的迅速发展，通信电源要求更大的输出电流和更小的输出电压纹波。对低压大电流输出的变压器而言，中心抽头不仅给变压器的没计和制造带来很大困难，而且外部引线的安装和焊接也很难处理。

常用的倍流整流电路拓扑如图l（b）所示，与传统的变压器副边带中心抽头的全波整流电路相比，倍流整流电路有以下优点：减小了变压器副边绕组的电流有效值；变压器利用率较高，无需中心抽头，结构简单；输出电感纹波电流抵消可以减小输出电压纹波；双电感也更适合于分布式功率耗散的要求。

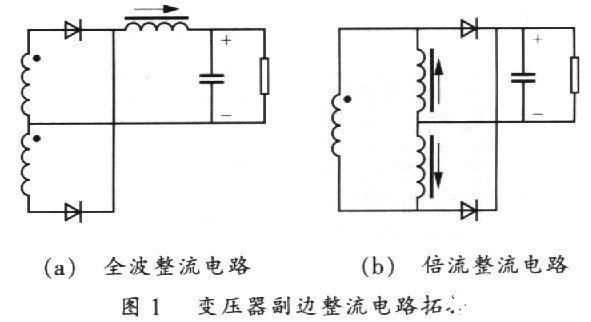
与全波整流电路相比，倍流整流器的高频变压器的副边绕组仅需一个单一绕组，不用中心抽头；与全桥整流电路相比，倍流整流电路使用的二极管数量少一半。因此，倍流整流电路结合了全波整流电路和全桥整流电路两者的优点。当然，倍流整流电路要多使用一个输出滤波电感，结构略显复杂。但此电感的工作频率及输送电流均为全波整流电路所用电感的一半，因此可做得较小。

2 工作原理

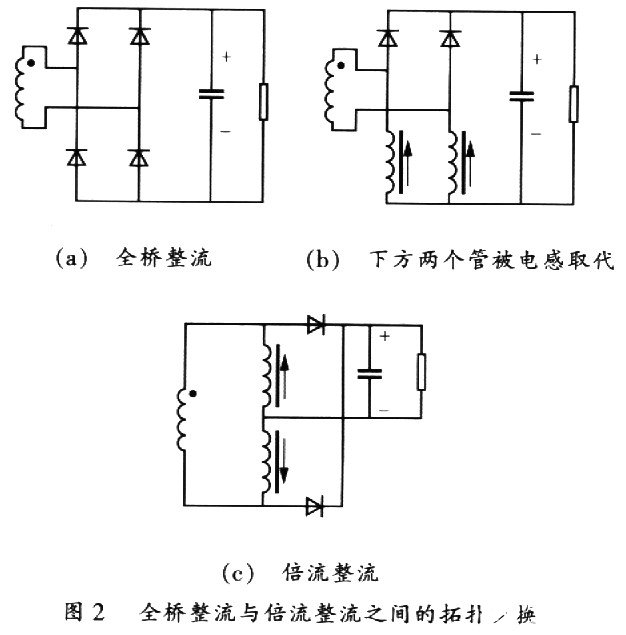
倍流整流电路可以被看成是由传统的全桥整流电路演变而来。如图2所示，将图2（a）中全桥整流电路中的两个下方二极管用两个电感取代，即可获得图2（b），经过整理后即可得到如图2（c）所示的倍流整流电路。

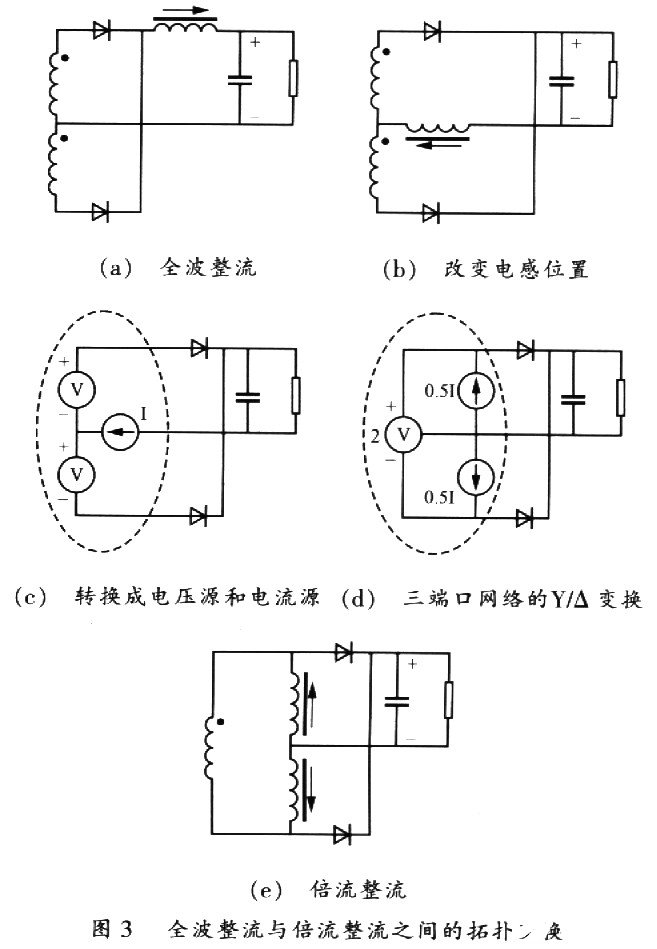
实际上倍流整流电路也可以由全波整流电路通过拓扑变换得来。在图3（a）中，输出电感与输出电容和负载电阻串联，而串联连接的兀件可以互换位置，因此将输出电感换到输出负母线，可得图3（b）；将变压器的副边绕组看成电压源，而把输出电感看成电流源，可得图3（c）；由虚线框内三端口网络的Y/△变换，可得图3（d）；再将电流源恢复成输出电感，将电压源恢复成变压器的副边绕组，可得图3（e）所示的倍流整流电路。

倍流整流电路的原理图如图4所示，对中、大功率的通信电源而言，移相全桥电路是较为常见的电路拓扑形式，在原边电路处于续流状态时，变压器的原边绕组和副边绕组都被短路。因此倍流整流电路在稳态运行时，每个开关周期有4种工作模式。为便于分析作如F假设：高频变压器原副边匝比为n=N1/N2，忽略高频变压器原副边漏感，所有器件均为理想器件。可得关键波形如图5所示。

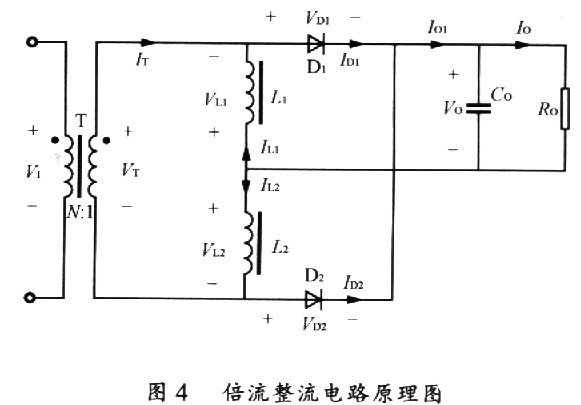
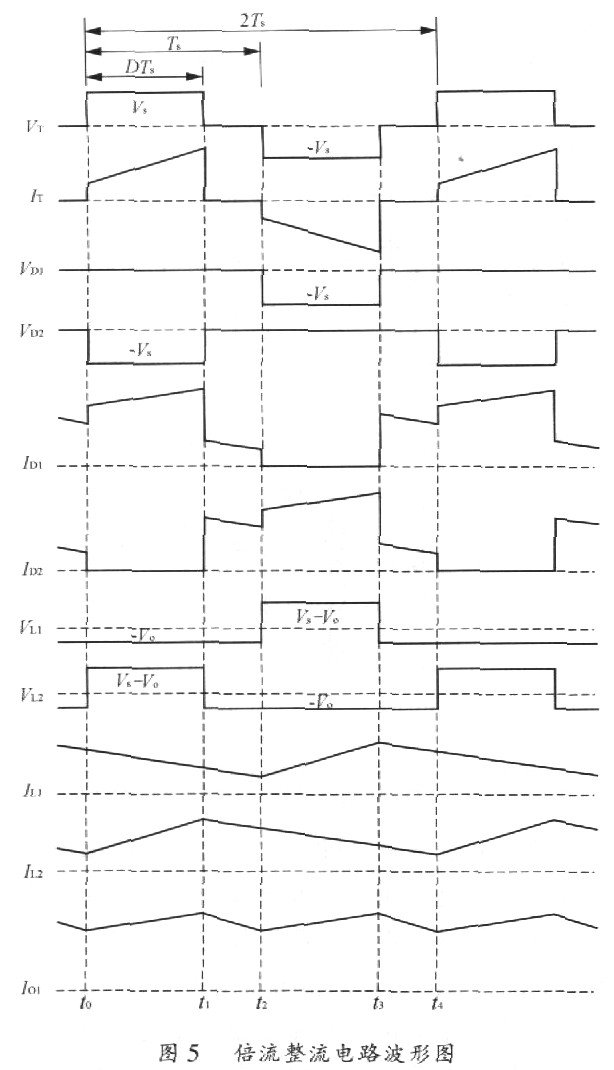
模式l［t0～t1］ 变压器副边电压VT为VS，电压极性为正，两个滤波电感的电流IL1和IL2极性都为正，二极管D1正向偏置导通，而D2反向截止。电感L1的电流IL1经二极管D1和输出电容C0续流，电感L1上的电压VL1为一Vo，极性为负，因此电流IL1线性减小，下降斜率由输出电压Vo和电感L1的比值决定。变压器副边电压VT通过二极管D1和输出电容Co加到电感L2上，因此电感L2上的电压VL2为VS-Vo，极性为正，电流IL2线性增加，上升斜率由变压器副边电压与输出电压的差VS一V0和电感L2的比值决定。变压器的副边电流IT等于IL2，电流I01为两个滤波电感电流的和IL1+IL2，由于输出大电容Co的滤波作用，输出电流I0为I01的直流分量。变压器的副边电流IT等于IL2。

模式2［t1～t2］ 变压器副边电压VT为0，两个滤波电感的电流IL1和IL2极性都为正，二极管D1和D2均为正向偏置导通。电感L1的电流IL1经二极管D1和输出电容Co续流，电感L1上的电压VL1为一Vo，极性为负，因此电流IL1线性减小，下降斜率由输出电压Vo和电感L1的比值决定。电感L2的电流IL2经二极管D2和输出电容Vo续流，电感L2上的电压VL2为一Vo，极性为负，因此电流IL2线性减小，下降斜率由输出电压Vo和电感L2的比值决定。变压器的副边电流IT等于O。

模式3［t2～t3］ 变压器副边电压VT为一VS，电压极性为负，两个滤波电感的屯流IL1和IL2极性都为正，二极管D1反向截止，而D2正向偏置导通。变压器剐边电压VT通过二极管D2和输出电容Co加到电感L1上，因此电感L1上的电压VL1为VS—V0，极性为正，电流IL1线性增加，上升斜率由变压器副边电压与输出电压的差VS一V0和电感L1的比值决定。电感L2的电流IL2经二极管D2和输出电容Co续流，电感L2上的电压VL2为一Vo，极性为负，因此电流IL2线性减小，下降斜率由输出电压Vo和电感L2的比值决定。变压器的副边电流IT等于一IL1。

模式4［t3～t4］ 与模式2的工作状态相同，变压器副边电压VT为O，两个滤波电感的电流IL1和IL2极性都为正，二极管D1和D2均为正向偏置导通。电感L1的电流IL1经二极管D1和输出电容Co续流，电感L1上的电压VL1为一Vo，极性为负，因此电流IL1线性减小，下降斜率由输出电压Vo和电感L1的比值决定。电感L2的电流IL2经二极管D2和输出电容Co续流，电感L2上的电压VL2为一Vo，极性为负，因此电流IL2线性减小，下降斜率由输出电压Vo和电感L2的比值决定。变压器的副边电流IT等于0。

由此可见．倍流整流电路的变压器副边平均输送电流仅为输出负载电流的一半。当一个电感在高频变压器副边的电压驱动下通过副边输送一半负载电流时，另一个电感也输送着相对于输出负载电流相同方向的另一半续流电流．且此续流电流不通过副边绕组。滤波电感平均输送电流仅为输出负载电流的一半，输出负载电流由两个电感同时分担，每个滤波电感的工作频率都等于高频变压器的工作频率。

3 设计要点

3．1 输出电压增益

由于电感在稳态运行时应该满足伏秒平衡条件，即电感电压丌关周期平均值为O，故

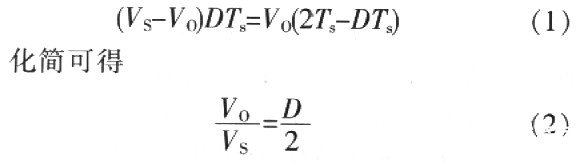
其中占空比D的取值范嗣为O≤D≤1。显然，与副边带中心抽头的全波整流器相比，倍流整流器的变压器具有相同的副边总匝数。

3．2 输出纹波电流对消

每个输出电感电流的峰峰值为

在占空比D的取值范围|0，1|区间内，随着占空比的增大，纹波电流对消因子越小。当D为0．667时，输出电流I01的纹波分量△I01为O．5△IL1；当D为1时，两个输出电感的纹波电流可以实现完全对消，输出电流I01的纹波分量△I01为0。

3.3 频域模型

采用状态李问平均法来推导倍流整流电路的数学模型，假设两个输出电感电流连续且极性都为正。考虑到动态中占空比是变动的，特用小写d来表示。

（1）在0≤t≤dTs期间

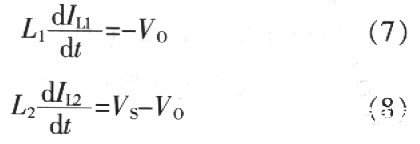
在倍流整流电路中，两个输出差模电感的值通常设计成相等，即L1=L2，因此上述方程组可以简化为

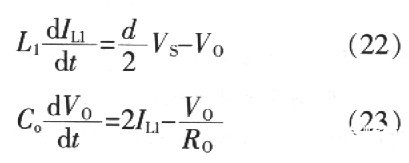
可以得到从占空比d到电感电流IL1的传递函数为

与全波整流电路相比，倍流整流电路的被控对象数学模型的零点相同而极点小同。如果引入等效输出电感Leg，看成是两个输出电感的并联，并且令

此时倍流整流电路被控对象数学模型的零点和极点都与全波整流电路相同。

根据七述频域数学模型，借助Matlah软件，可以比较容易地利用波特图等传统方法对控制器进行设计。

4 结语

本文对通信电源中使用的倍流整流电路的工作原理进行了详细描述，指出了倍流整流电路与全波整流电路和全桥整流电路之间的区别和联系，对倍流整流电路的输出电压增益和输出纹波电流对消给出了定量描述，应用状态空间平均法对倍流整流电路的被控对象数学模型进行了推导，为控制器的设计提供了理论基础。

责任编辑：gt