

小型化SIR同轴腔体滤波器的设计
EDA/IC设计
描述
小型化SIR同轴腔体滤波器的设计
微波带通滤波器是无线电通信系统中的一类关键无源器件。近年来,随着微波技术的迅速发展,无线电通信频率资源日益紧张,这就对滤波器的性能指标提出了更高的要求,因此研究新的高性能微波带通滤波器具有十分重要的实际意义。而同轴腔滤波器具有功率容量大、体积小、Q值高、易于实现的特点,能够符合带内插损小、带外抑制高的设计要求。λg/4型阶跃阻抗变换器(SIR)作为基本谐振单元在不减小无载Q值的情况下,可减小滤波器尺寸,并通过调节阻抗比来较好地控制杂散频率。同时采用梳状线的形式,由于一端的电容加载,进一步缩短了谐振器的尺寸。SIR滤波器在结构和设计上有很大的自由度,通过采用不同类型的传输线(同轴、带状线、微带、共平面)或介电材料而使其有很大的应用频率范围。
1 基本原理
SIR是由两个以上具有不用特征阻抗的传输线组合而成的横向电磁场或准横向电磁场模式的谐振器,包括λg/4型、λg/2型和λg型,都有开路面、短路面和它们之间的阻抗阶跃接合面。图1为λg/4型SIR结构。

传输线开路端和短路端之间的特征阻抗和等效电长度分别对应为Z1、θ1和Z2、θ2,输入端的阻抗和导纳分别定义为Zi和Yi。若忽略阶跃非连续性和开路端的边缘电容,那么Zi的表达式如下

当Yi=0时,可得谐振条件为
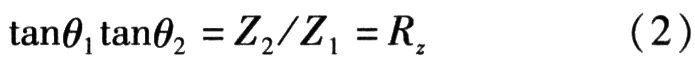
由此可得谐振条件取决于θ1、θ2和阻抗率Rz。一般均匀阻抗谐振器(UIR)的谐振条件唯一取决于传输线的长度,而对SIR同时要计人长度和阻抗比。因此SIR比UIR多了一个自由度。图2是同轴SIR的基本结构,内导体的半径和长度分别为a1、l1和a2、l2,外导体内半径为6,整个SIR总的电长度可表示为θr,则阻抗比Rz可以表示为


以θ2=θ2-θr代人式(2)并求解,得

为了实现小型化设计,要求0

上述计算表明,θ1=θ2=θ0是一个特殊条件,并且(θT)min是随着Rz的减小而减小,对谐振器的长度压缩就越大。滤波器的杂散频率由阻抗比由Rz决定。
(2 设计实例
该同轴腔梳状带通滤波器的技术指标要求为:中心频率f0=751 MHz,带宽BW=13 MHz,带内插损L0<1.0 dB,带外衰减>30 dB,在f0±20 MHz,腔体高度<40 mm。
由文献[3]查表可知:n:6,g1=2.154 6,g2=1.104 1,g3=3.063 4,g4=1.151 8,g5=2.993 67,g6=0.810 1。
2.1 单腔谐振单元的物理尺寸
中心频率为751 MHz,1/4波长大约为100 mm,普通梳状线电容加载的滤波器的单个谐振器的尺寸为1/8波长约为50 mm,而要求腔体高度小于40 mm。在本实例中,采用在SIR结构中加载电容的方式。设定谐振腔长度为34 mm,谐振器总长lT为32 mm,对于空气填充的λg/4型SIR谐振腔,在θ1=θ2=θ0的条件下,可以确定l1=21 mm,可得Rz=tan2βl1=tan22πl1/l0=0.11,其中l0为空气中波长。
通带中心插损 要求L0<1.0 dB,因此未加载Q值为:Q0>1 538.3,由知
要求L0<1.0 dB,因此未加载Q值为:Q0>1 538.3,由知 ,(b的单位为cm),得到b>0.85 cm,取b=9 mm。为了取得最大的Q值,Z1取值范围应该为75~90 Ω,因此可以将内导体半径分别确定为:a1=2.3 mm,a2=7.7 mm。由于阶跃结合面和开路端电容的不连续性与谐振器之间形成的耦合电容,以及电容加载的影响,故阶跃结合面与开路端的边缘电容和加载电容可以用一段等效的长度△li来代替。这样可以得到l2=l1-△lj,其中△lj≈Cfln(b/a1)/2πε0,Cf=Cfe+Cb,Cfe为端壁边缘电容,计算式见文献[2],Cfs为边壁边缘电容计算式同文献[5]中梳状线带通滤波器的集总电容的计算。得到△lj=12 mm,则l2=9 mm。通过HFSS单腔本征模的仿真,可以得到最终尺寸a1=2 mm,a2=8 mm,l1=24 mm,l2=8 mm,如图3所示。
,(b的单位为cm),得到b>0.85 cm,取b=9 mm。为了取得最大的Q值,Z1取值范围应该为75~90 Ω,因此可以将内导体半径分别确定为:a1=2.3 mm,a2=7.7 mm。由于阶跃结合面和开路端电容的不连续性与谐振器之间形成的耦合电容,以及电容加载的影响,故阶跃结合面与开路端的边缘电容和加载电容可以用一段等效的长度△li来代替。这样可以得到l2=l1-△lj,其中△lj≈Cfln(b/a1)/2πε0,Cf=Cfe+Cb,Cfe为端壁边缘电容,计算式见文献[2],Cfs为边壁边缘电容计算式同文献[5]中梳状线带通滤波器的集总电容的计算。得到△lj=12 mm,则l2=9 mm。通过HFSS单腔本征模的仿真,可以得到最终尺寸a1=2 mm,a2=8 mm,l1=24 mm,l2=8 mm,如图3所示。

2.2 终端Q值
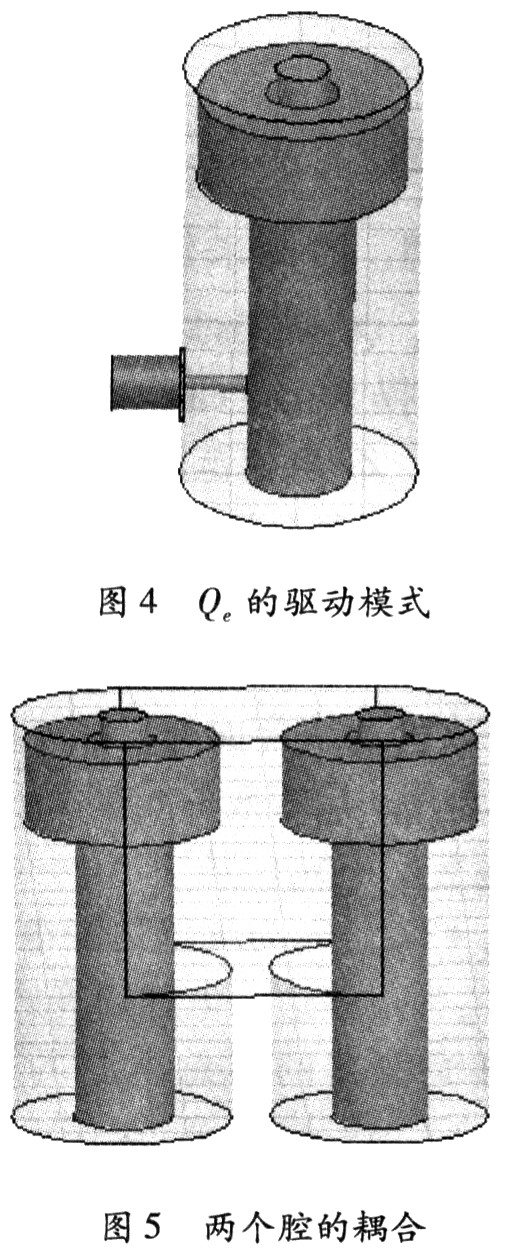
终端外界Q值就是终端电阻反射到第一个谐振器中所得到的Q值。Qe值在理论上可以从低通原型参数和滤波器指标中获得,第一个谐振器的Qe=gog1Ω/BW=53.865。同时Qe还可以通过S11在谐振频率处的群时延来提取。通过单腔驱动模式的仿真计算得到S参数,根据公式Qe=ω0τs11(ω0)/4,由此可得激励的高度为7.4 mm,如图4所示。另外,从耦合矩阵中得出耦合系数,通过改变耦合孔的高度来改变耦合量的大小,达到所要求的耦合系数,如图5所示。
最后经HFSS仿真优化,结果如图6和图7所示。


3 结束语
文中以同轴SIR谐振器为单元,谐振器间采用开窗口的形式形成电容和电感耦合构成滤波器结构,设计了一款小型化的梳状带通滤波器,并在谐振器的开路端加载电容。由于加载电容及阶跃电容的存在,使其尺寸《1/4波长,与1/4波长100 mm相比,长度压缩了66%,软件仿真结果验证了该方法的可行性和有效性。
-
同轴腔体窄带带通滤波器快速设计方法2023-12-14 4372
-
一种新型小型化窄带腔体滤波器的设计2023-12-16 3545
-
P波段腔体滤波器的小型化设计2024-01-02 3225
-
怎么设计小型化宽阻带微带带通滤波器?2019-08-22 2033
-
WLP-BAW滤波器的热建模功率容量与小型化,不看肯定后悔2021-06-08 2623
-
EPCOS推出性能出色的小型化蓝牙和GPS用2合1滤波器2009-08-11 654
-
小型化电容加载腔体滤波器设计2013-01-10 1235
-
腔体滤波器生产厂家2017-10-25 10658
-
小型化LTCC宽带带滤波器2018-01-24 1112
-
同轴滤波器详解2018-02-08 5788
-
采用DC-SIR结构实现双同轴腔体滤波器的应用方案2021-05-31 3524
-
腔体交叉同轴滤波器设计2021-06-07 1075
-
滤波器小型化设计概述 不同类型的滤波器设计2023-02-17 1671
-
腔体滤波器和介质滤波器的区别2023-02-27 5107
-
低频段高抗振大功率滤波器的小型化设计2023-12-10 3000
全部0条评论

快来发表一下你的评论吧 !

