

基于频域处理法实现数字音频的变调功能
描述
1 引言
改变声音信号的音调是许多商用设备的一种功能,最典型的应属卡拉OK机了。由于发音音调高低因人而异,人们希望伴奏音乐的音调适合自己的嗓音,因此卡拉OK机中设计了专门的硬件来实现这一功能。例如雅马哈公司的用于数字变调的大规摸集成电路 YSS222D和YSS216B,内部集成了A/D,D/A和数字信号处理器,利用采样和重放数据时速度的不同来实现变调。功能,重放比采样速度快则升调,反之则降调。另外,为了使播放时间不变,还需对数据段进行复制或删除。由于商业保密的需要,具体算法未公开,据可询资料实现的系统,不能有效解决因复制或删除数据带来的相位不连续问题。
当前,声卡已成为计算机的基本配置,但无变调功能,为弥补这一缺憾,可以采用件的方法对声音文件重新编码,使声卡回放时音调改变。另外,数字音频工作站也需要软件实现变调功能。因此讨论了3种软件实现算法,围绕着如何变调而不变时间,以及如何解决相位不连接问题,从变调原理着手,讨论了时域实现的理论依据,最后找到了一种有效的变调方法-- 频域处理法,实验证实效果良好。
2 变调的乐理基础
声音是由物体振动产生的,声音的基本要素有:音调、音强和音色。乐音体系根据振动频率即音调的不同,将乐音分成音级,基本音级广泛采用CDEFGAB这8个字母命名,某音级与往上数8个音级之间的距离称为“纯八度”,世界上普遍采用的12平均律将一个纯八度分成12个均等的半音,相邻两个半音间的物理振动频率相差21/12倍,也就是说各半音间的振动频率成等比关系,一个纯八度频率相差2倍。
如果将信号中的所有频率成分升高或降低21/12倍,就能使音调升高或降低一个半音。假设原信号频率为f,变调后频率为f,二者的关系应该满足
f=fx2d/12, d=±1 ,±2,±3 (1)
当d》0时,升调,反之,降调;d每变化1,音调升高或降低一个半音。
3 时域实现的依据及存在的问题
一种实现变调的作法,是采用硬件实现相似的办法,即改变WAV文件头中有关采样率的信息。如果采样率提高,则声卡回放速度加快,产生升调的效果,同时回放时间变短;反之,产生降调的效果,回放时间变长。为保持时间不变,以帧为单位,利用信号的短时周期性,升调时将帧内后部数据段复制,降调时将帧内后部数据段删除,图1画出了一帧的数据处理情况。可以看到,若是升调,帧间数据是连续的,但由于数据段的复制,帧内数据段间相位不连续;若是降调,帧内数据连续,但帧间数据相位不连续,因此声音质量必然受到影响,产生喀嚓声。
另一种方法是,采用时域抽选和内插[4]。下面分析抽选和内插的频谱,看如何实现变调。抽选表示成下式
Xd[n]=[nM] (2)
表示每M个采样值选1个,其余M-1个舍弃,则信号长度缩短为1/M。抽选后信号频谱和原信号频谱间的关系为
1 M-1
Xd(ejω)=-Σ X[ej(ω/M-2πi/M (3)
M i=0
图2所示粗线为M=2的抽选信号频谱,粗实线为M=2的抽选信号频谱,可以看出,抽选后信号的频率成分均为原来的2倍,所以能实现升调。为防止抽选后频谱混叠,抽选前必须作抗混叠数字低通滤波,截止频率为π/M。
再看看内插的频谱变化。内插时域表示成
Xi[n]={x[n/L,n=O,±L,+2L,+3L, 。.. (4)
0, 其它
表示每两个采样值中插入L-1个零,整个信号长度增加为L倍。内插后信号频谱和原信号频谱间的关系为
Xi(ejω)=X(ejLω) (5)
图2虚线所示为L=2的内插信号频谱,可以看出,所有频率成分均为原信号的1/2,所以能实现降调。为不产生镜像频率成分,内插后必须作反镜像数字低通滤波,截止频率π/L,也可用线性内插取代插零,而无须反镜像滤波。
抽选和内插后的数据量同样会变短或变长,下面来推导保持数据量不变的具体实现方法。根据上述抽选和内插的频谱变化情况,反推时域变化过程:若将信号作快速离散傅里叶变换(FFT),将谱线沿频率轴扩张或收缩,再作反变换(IFFT),得到的信号应该是被升调或降调,并且数据量保持不变。
非整数倍的变调可由抽选和内插结合实现,同样可以采用数据段的复制或删除的办法保持数据量即回放时间不变,其系统结构如图3所示。但对于复制或删除数据后段间相位的不连续性问题,有些资料[3]提出找出信号的基音周期,以基音周期为复制或删除单位,并帧间重叠处理,也不能从根本上解决相位问题。
4 频域实现的算法研究
现在考虑采用频域实现来解决相位问题。
首先采用频谱伸展的办法得到升调的信号,如图4所示,(a)为原始信号波形及FFT的幅度和相位图,(b)为将原始信号的FFT谱线向高频伸展一倍,中间内插零,再IFFT得到信号波形及FFT幅度和相位图,情况和时域抽选一样。然后考虑将频谱伸展过程中的谱线内插零改成线性内插,如(c)所示,可见信号波形段间能很好地吻合,但波形失真较大。最终发现结合插零和线性内插,低频插零,高频线性内插,既能保证波形失真较小又能在两段相连处较好地过滤,如(d)所示。
对于降调,图5(a)是2帧原始信号波形及后一帧的FFT幅度图,图5(b)采用FFT谱线向低频收缩,再IFFI,得到的波形和时域内插法一样,改进措施见图5(c),被处理的连续两帧信号间有一部分重叠,得到的两帧信号波形便能很好地过渡。
因此,要实现式(1)任意倍频率的变调,令α=2d/A2,采用以下公式。为简单起见,低频高频均线性内插:
X[K]=FFT[x(n)], k=0,1,。..N-1 (6)
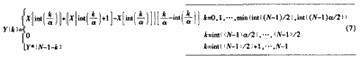
y[n]=IFFT[Y(K)],n=0,1,。..N-1 (8)
其中N是帧长,int()表示取整,min()表示取较小值。注意,仅仅对于降调a
另外帧长,即被处理的数据长度也必须适当,如果太短,会造成数据的复制和删除太过频繁;过长,又不符合短时周期性,明显地感到声音的多次重复或被打断。经过实验表明,帧长取4000点左右比较合适,对于采样率44.1 kHz的音频信号是0.1 s的数据量,4 000点的FFT使频谱取样间隔为10Hz左右。
5 结束语
实现变调的基本原理是改变信号的频率成分,可以通过时域抽选或内插实现,但为保持时间不变,每帧要复制或删除部分数据段,由此带来相位不连续从而影响声音质量。文中提出的频域法,根据变调的原理,将FFT谱线向高频或低频搬移,再作IFFT得到时域信号,若升调谱线搬移过程中采用线性内插,降调采用时域帧间重叠,能消除数据段的不连续问题,改善变调后的声音质量。频域实现无须低通抗混叠滤波或低通反镜像滤波,且FFT是快速算法,假设采用如ADSP2181或TMS320C54X,乘法运算占用单指令周期的DSP芯片,运算量小于1 MIps,实时运算不成问题。可见,频域法是一种有效可行的办法。
责任编辑:gt
-
数字音频输入接口电路2009-08-01 0
-
数字音频接口的优势是什么2021-03-09 0
-
面向高清电视的全数字音频系统的设计2009-12-02 616
-
数字音频监测系统设计及应用2010-07-07 499
-
数字音频编码技术2010-08-31 784
-
一种基于SOLA的数字音频变调算法及其在TMS320C6712010-09-01 686
-
数字音频编辑技术2010-09-13 531
-
数字音频监视器2010-12-19 656
-
什么是DAB/数字音频广播2010-01-28 2238
-
什么是数字音频2010-02-02 4177
-
什么是数字音频会议系统?2010-02-21 1064
-
面向高清电视的全数字音频系统2012-07-16 1554
-
数字音频应用解析2017-11-01 6841
-
数字音频技术的应用与发展2024-07-13 2164
-
电视数字音频输出是什么接口2024-09-24 2426
全部0条评论

快来发表一下你的评论吧 !

