

ARIMA时间序列模型的建立及在半导体行业领域的应用
描述
作者:钮轶君,钱省三,任建华
1 引言
当今半导体产业面临全球化的巨大挑战,不但存在行业内部企业之间的竞争,行业与行业之间的竞争也日益激烈,直接导致市场需求不确定因素急剧增加;另外,近年来半导体产品的生命周期日趋缩短,这又直接增大了该产业市场需求预测的难度,因此,需求预测管理成了半导体制造企业运营过程中重要的环节。
据iSupply的研究统计,目前有高达70%的晶圆厂不能进行较为准确的需求预测。这将引发企业交期延误、资产周转率减缓、库存过剩及成本增加
等危机。半导体产业分工细微,上中下游程序息息相关,建立有效的订单预测管理体系可降低需求预测误差带来的风险,使得企业获得更多的市场份额,并提升自身的订单交货率和顾客满意度。
本研究拟建立ARIMA (autoregressiveintegratedmovingaveragemodels)时间序列模型,并针对我国某半导体晶圆厂进行实例研究,旨在帮助晶圆代工厂准确而弹性地满足顾客需求并实现最大化利润。
2 ARIMA模型简介
Box和Jenkins(1977)首次提出了一种时间序列预测分析方法,自回归求和滑动平均过程,简称ARIMA(p,d,q)。其中,p为自回归项数,q为滑动平均项数,d为使之成为平稳序列所做的差分次数(阶数)。ARIMA模型主要应用于需求预测。
2.1 自回归求和滑动平均模型(ARIMA)
ARIMA包含了三种模型:autoregressive(AR)、movingaverage(MA)和ARMA。运用ARMA模型的前提条件是,用作预测的时间序列是由零均数的平稳随机过程产生的。
所谓由平稳随机过程产生的时间序列具有以下性质:(1)概率分布函数不随时间变化;(2)期望值、方差和自协方差是不依赖于时间的常数。
随机时间序列模型必须以时间序列的平稳性为基础建立。时间平稳性反映在图形上就是时间序列数据的自相关系数在某一固定水平线附近摆动,且按周期性逐渐衰减。所以对于某些不平稳的时间序列必须经过差分变换,使其转化成平稳的时间序列。
如果经过差分变换后的时间序列再应用ARMA模型,习惯上称该序列为ARIMA模型,该模型定义为
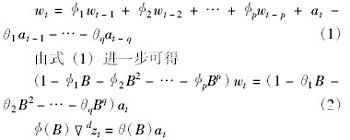
式中,B为后移算子,▽为差分算子。记为Bkzt=zt-k。这样,一个非平稳时间序列经过d次差分后转化成一个平稳的时间序列,然后就可以用平稳的时间序列模型ARIMA来表示。
2.2 ARIMA乘积模型
对于一些以月、季度为时间单位的序列来说其时间序列分析是有季节变化的。季节模型和连续模型一样,只是连续模型的时间单位是1,而季节模型的时间单位是相应的周期s。
在实际情况中,往往一个季节性时间序列不仅仅有季节性成分还会含有非季节性成分;或者说既包含不同周期间的变化情况,还包含同一周期中不同观察值的变化情况。这时可用ARIMA乘积模型进行预测可以获得较为满意的结果。
ARIMA乘积模型的数学表达式为
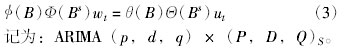
记为:ARIMA(p, d, q) × (P,D,Q)S。
2.3 ARIMA乘积模型的模型识别方法
ARIMA乘积模型的自相关函数(ACF))和偏自相关函数(PACF)性质见表1,可以据此判断该模型中各参数的选取。

3 实例研究
本实例主要利用SPSS13.0对产品C建立ARIMA模型。以2001年1月~2006年6月某半导体制造厂A公司的产品C实际销售数据为基础。其中2001年1月~2005年12月的历史订单数据将被用以建立预测模型,而2006年1月至2006年6月的实际销售数据则作为判断对该模型预测效果好坏的评判标准。
3.1 判断模型时间序列的平稳性
设定参数d,D。绘制产品C历史需求量的序列图。产品C的历史需求数据呈周期状波动,周期为1年,这是由于半导体产业的景气循环造成的。因此考虑采用ARIMA (p,d,q)×(P,D,Q)S季节模型进行预测,通过一次差分和一次季节差分将原产品C的销售量时间序列转化成平稳序列,即d取1,D取1。
3.2 判断时间序列的ACF和PACF特征
设定参数p,q,P,D;从所得的候选模型中判断选出最合适的预测模型。利用表1所示的ARIMA模型识别方法,选出产品C的9个需求预测候选模型。AIC和BIC是信息选择值。
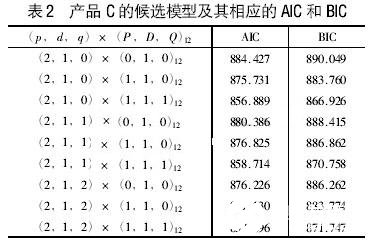
根据表2所示,选出AIC和BIC值皆最小的候选模型组合(2,1,0) ×(1,1,1)12,作为产品C的需求预测模型。从所选模型的残差自相关函数图和残差偏自相关函数图中可以看出,该候选模型下,自相关图和偏自相关图皆不显著,所以产品C的残差为“白噪声”序列。
3.3 对所选出的产品C预测候选模型进行参数估计、假设检验和模型诊断
ARIMA模型中,误差项序列必须正态且相互独立,因此必须对订单预测候选模型进行残差检验,以确定该模型的误差项是否为“白噪声”序列,如不是的话,则要对该候选模型进行修正。由前K个残差自相关系数^γ1,…,^γk组成的统计量Q,即

式中: ^γk为残差自相关系数;T为时间序列的观察值个数。统计量Q是均值为0方差为1/T的独立正态随机变量的平方和。Box和Pierce证明了其近似程度非常高,且统计量Q服从自由度为K-p-q的χ2分布。
对于产品C,有
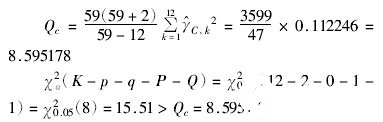
因此产品C取ARIMA (2,1,0) × (1,1,1)12模型可以通过χ2 检验。运行SPSS软件的ARIMA分析模块即可得到产品C的需求预测模型表达式为
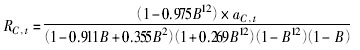
式中: aC,t为白噪声残差序列; B为后移算子。其中ΦC,1=0.911,ΦC,2=-0.355,ΦC,1=-0.269,ΘC,1=0.975。
3.4 判断产品的预测效果
判断产品产品C取ARIMA (2,1,0) × (1,1,1)12模型的预测效果比较,见图1。
从图1可以看出,产品C取ARIMA(2,1,0)×(1,1,1)12模型时,可以获得和实际销售量情况较一致的预测效果。所以产品C的需求预测模型即为ARIMA(2,1,0) × (1,1,1)12。
4 结论
半导体产品需求变化很大,因此对其进行较为准确的预测将帮助企业更好的进行各种生产决策和库存决策,有效地避免了库存积压和供需失衡现象出现给企业带来的损失。
利用ARIMA模型进行需求预测具有精度高、数据可靠、操作方便、运行迅速、应变能力强等优点,但从模型本身的构建原理来看,该时间序列模型只适合于作短期预测,不适合于作长期预测。如果企业能对半导体市场需求进行较为准确的预测,同时结合供应链环境制定出切实准确的生产决策,可以从很大程度上提高企业以及其合作伙伴的收益。
责任编辑:gt
-
【《时间序列与机器学习》阅读体验】+ 时间序列的信息提取2024-08-14 982
-
大模型在半导体行业的应用可行性分析2025-06-24 1669
-
创新是半导体行业新一轮增长的关键2011-03-22 2968
-
labview arima model的模型怎么建立2013-02-18 2011
-
安森美半导体宣布收购Fairchild半导体2018-10-31 4799
-
自回归滞后模型进行多变量时间序列预测案例分享2022-11-30 2607
-
ARIMA模型在期货交易预测中的应用研究2009-08-19 648
-
算法大全_时间序列模型2016-01-14 649
-
基于多尺度小波分解和时间序列解决风电场预测精度等问题2017-10-21 895
-
基于模糊时间序列定义论域方法2017-10-28 777
-
基于ARIMA-GARCH模型的超短期风速预测2017-12-26 1190
-
基于动态时间弯曲距离的长期直觉模糊时间序列预测2018-02-08 1066
-
利用ARIMA时间序列模型满足半导体市场需求并实现最大化利润2021-01-20 2874
-
做时间序列预测是否有必要用深度学习2022-03-24 2325
-
arimagarch模型怎么预测2024-07-09 1331
全部0条评论

快来发表一下你的评论吧 !

