

浅谈经典磁性系统中的拓扑绝缘体和半金属一文
电子说
描述
自上世纪八十年代发现量子霍尔效应以来,人们逐渐认识到了一种新物相---拓扑相的存在,这种奇异的物相能使系统免于材料缺陷和无序的干扰,它所具备的鲁棒特性使得拓扑态在信息传输与量子计算领域产生了巨大的潜在应用价值。对拓扑相的研究虽然始于电子系统,但是近年来这一概念已经被拓展到了几乎所有物理学分支,如光学、声学、力学、电路和自旋电子学等。
拓扑理论中存在着一种非常重要的对应关系,即所谓的体边对应:体能带的性质决定边界态(表面态)的属性。传统的n维拓扑绝缘体具有n-1维拓扑边界态(表面态),被称为一阶拓扑绝缘体,如图1(a)所示。有趣的是,近两三年来,拓扑绝缘体的定义被推广到了高阶情形,即所谓的高阶拓扑绝缘体。和普通(一阶)绝缘体所不同的是,高阶拓扑绝缘体允许n-2甚至n-3维拓扑边界态的存在,如图1(b)和1(c)所示。对高阶拓扑相的刻画需要借助于一些新的拓扑不变量,如体极化、格林函数零点和贝里相等。
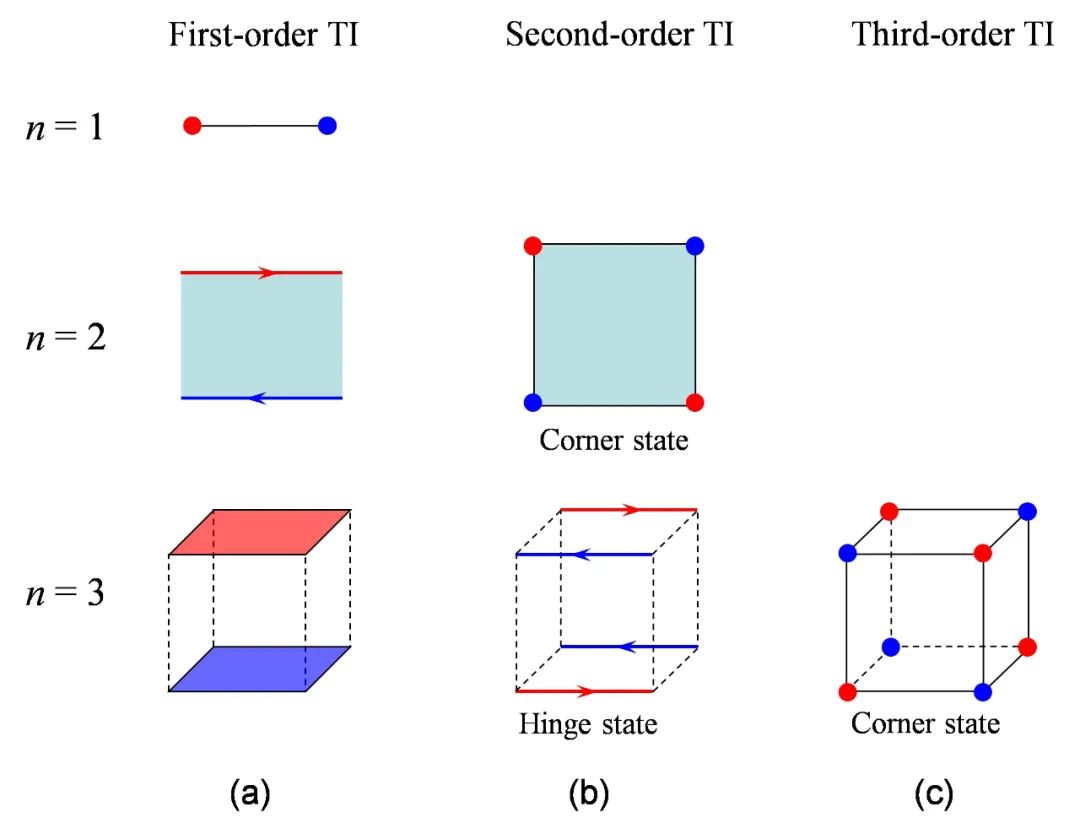
图1:不同类型的拓扑绝缘体。不同维度下,一阶(a)、二阶(b)和三阶(b)拓扑绝缘体及拓扑边界态特点。
在经典的磁性系统中,自旋波(或磁振子)和磁孤子(如畴壁、涡旋、斯格明子等)代表了两种重要的激发。类似于电子和光,磁振子和磁孤子也能作为载体实现对信息的操控、传输和处理,基于它们的器件具有高密度、低能耗和非易失等传统电子器件所无法企及的优势。但是一般的自旋电子器件容易受到材料中不可避免的缺陷和无序的影响,寻找磁性材料中的拓扑相有望成为解决这一问题的关键。2010年磁振子霍尔效应的发现揭开了人们研究磁振子拓扑相的序幕,最近人们又发现磁孤子阵列的集体振荡在一定的条件下也能表现出拓扑性质,基于磁振子和磁孤子晶体(或超材料)的拓扑绝缘体和半金属吸引了越来越多研究者的关注。
在此领域,电子科技大学电子学院、电子薄膜与集成器件国家重点实验室严鹏教授课题组已经取得了一系列前期重要成果[Phys. Rev. Lett. 124, 217204 (2020); Phys. Rev. Lett. 121, 197201 (2018); Phys. Rev. Res. 2, 022028(R) (2020); Phys. Rev. Applied 13, 064058 (2020); Phys. Rev. B 98, 180407(R) (2018); npj Comput. Mater. 5, 107 (2019); Nano Lett. 20, 7566 (2020)]。最近,严鹏教授课题组应邀在物理学综述期刊《物理报道》(Physics Reports)上在线发表长篇综述文章《经典磁性系统中的拓扑绝缘体和半金属》(“Topological insulators and semimetals in classical magnetic systems”)。李志雄博士为该论文的第一作者,严鹏教授为通讯作者,曹云姗副教授参与了指导。电子科大为该工作的唯一完成单位。该综述文章详细介绍了近十年来磁性系统中对磁振子和磁孤子拓扑相的研究现状,包括磁振子霍尔效应、拓扑磁振子绝缘体和半金属、拓扑磁振子器件、磁孤子系统中的(高阶)拓扑相等,同时也指出了本领域面临的挑战与机遇。
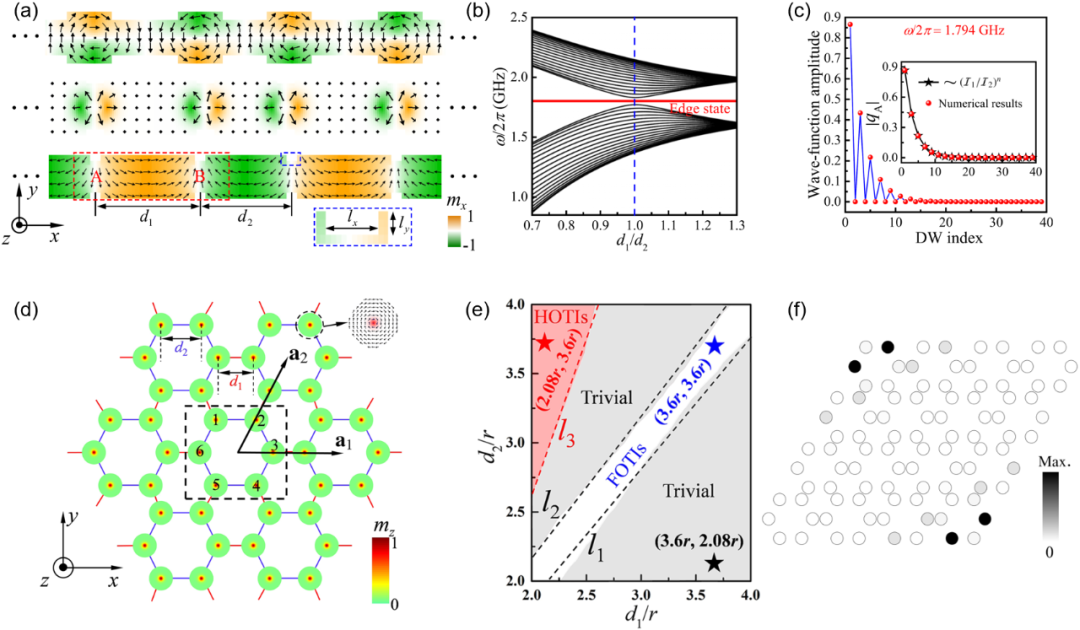
图2:(a)一维涡旋、斯格明子和畴壁晶体示意图。(b)一维畴壁晶体结构对应的能带。(c)边界态波函数强度的空间分布。(d)二维涡旋呼吸型蜂巢阵列。(e)系统的相图。(f)高阶拓扑边界态(角态)的波函数强度分布。
对磁振子的拓扑相的研究主要可以归结为如下方向:(1)基于不同晶格类型的拓扑磁振子绝缘体;(2)不同微观机制导致的磁振子非平庸拓扑相,如由于反演对称破缺导致的Dzyaloshinskii-Moriya 相互作用、磁偶极相互作用和磁性结构等;(3)狄拉克和外尔磁振子;(4)磁振子与声子耦合形成的拓扑磁振子极化子;(5)高阶拓扑磁振子;(6)基于磁振子的拓扑自旋器件,如磁振子二极管、磁振子分束器、磁振子干涉仪和磁振子逻辑门等。磁孤子作为磁性系统中的另一种重要激发,其拓扑相的研究还相对较少。对于一维磁孤子(以畴壁为例)系统 [如图2(a)所示],通过调节磁孤子之间的间距,系统可以实现一阶拓扑相,图2(b)给出了有限大小系统的能带结构,可以发现带隙中存在明显的简并模式,这些模式正是局域振荡的拓扑边界态,如图2(c)所示。如果考虑二维磁孤子(如涡旋)系统 [这里以呼吸型蜂巢结构为例,如图2(d)所示],通过调节两个几何参数d1和d2,系统可以在平凡相、一阶拓扑相和高阶拓扑相之间变换,相图如图2(e)所示。图2(f)画出了系统处于高阶拓扑相时对应的拓扑角态模式。总的来说,磁学系统中高阶拓扑相的研究还处在非常初级的阶段,很多相关的科学问题亟待解决。
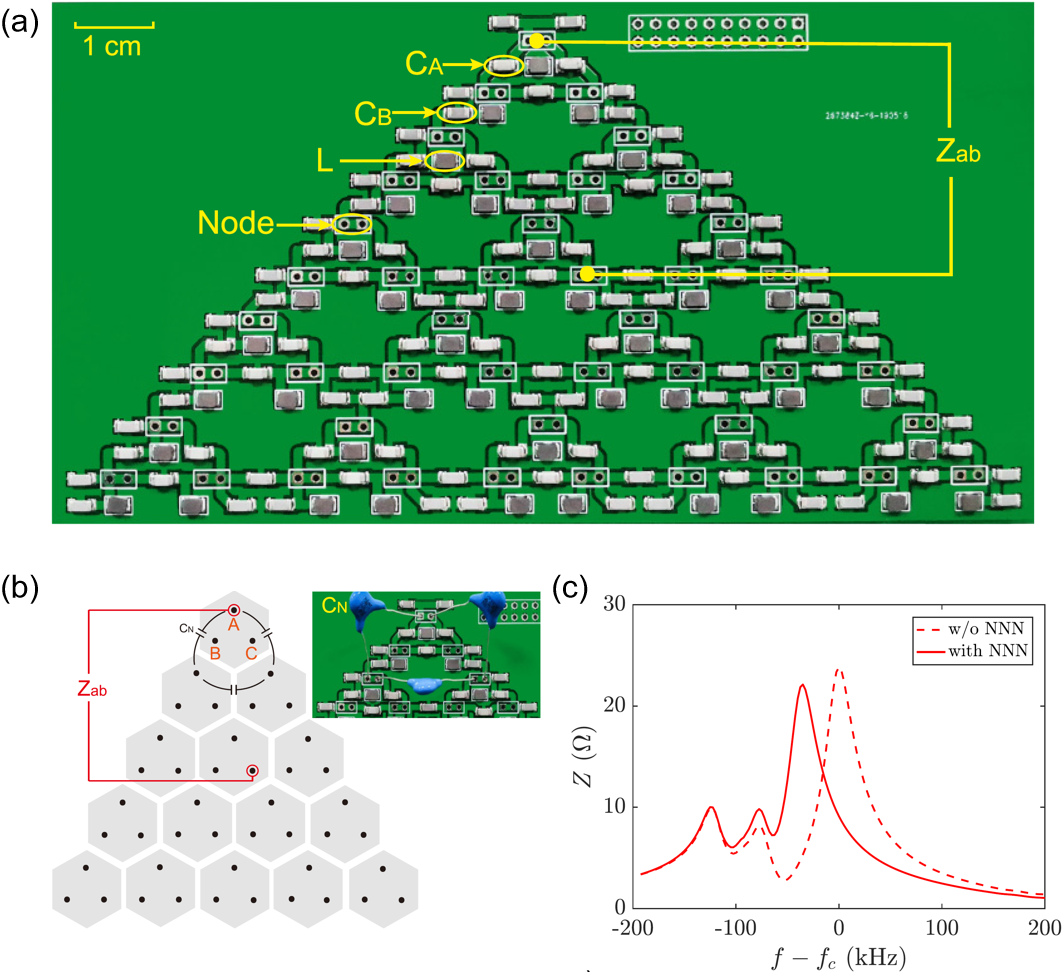
图3:(a)呼吸型kagome高阶拓扑电路。(b)在某个顶点引入次近邻相互作用,从而打破手征对称性。(c)实验测量结果(虚线和实线分别表示没有和有次近邻相互作用)。
值得一提的是,呼吸型晶体中出现的高阶拓扑相零能模一般受广义手征对称性的保护,这一性质可以通过实验上引入次近邻相互作用打破系统手征对称性,进而测量零能模是否有漂移来检验。但是,要在凝聚态系统中人为的引入次近邻相互作用是非常困难的,幸运的是近几年发展的拓扑电路系统能方便地解决这一问题(次近邻相互作用可以通过接入电容或电感来实现)。图3(a)画出了一种高阶拓扑电路模型(呼吸型kagome晶格),在某一个顶点上通过连接额外的电容从而破坏系统的手征对称性,如图3(b)所示。实验结果表明当系统手征对称性被打破时,高阶拓扑边界态的频率相比具有手征对称性时有了明显的偏移 [如图3(c)所示],这一实验结果很好的证实了手征对称性保护拓扑零能模的理论。
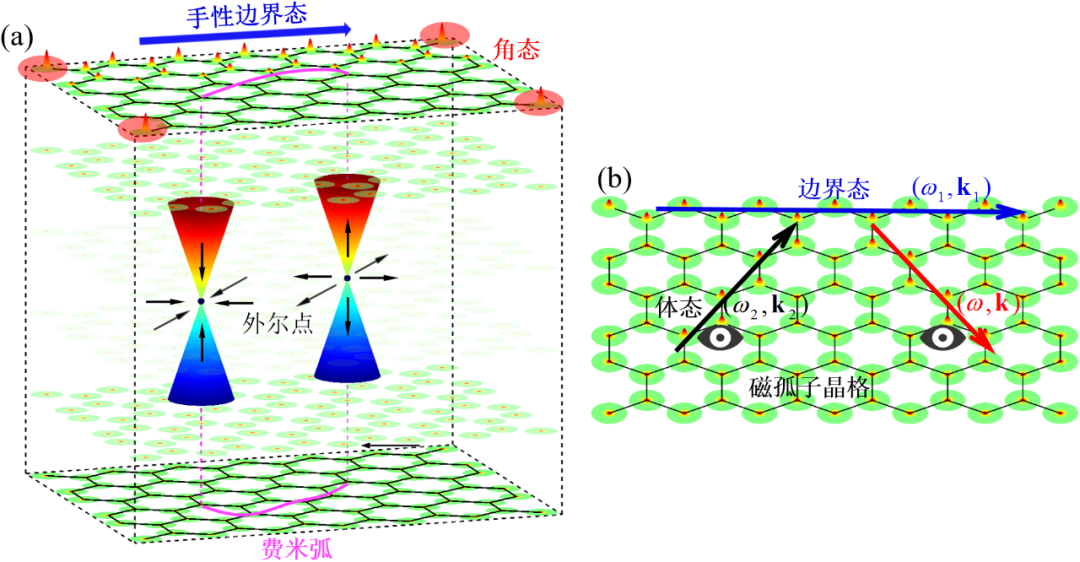
图4:磁孤子拓扑绝缘体和半金属。(a)磁孤子阵列中一阶和高阶拓扑绝缘相以及外尔半金属相的典型特点。(b)磁孤子系统中拓扑边界态的探测原理:通过测量入射和出射的磁振荡模式反推边界态频谱。
图4(a)画出了磁孤子系统中拓扑绝缘相(包括一阶和高阶)和外尔半金属相的典型特点,而磁孤子系统中拓扑边界态的探测可以通过如下方案实现:体态模式和边界态模式发生相互作用后,通过分析入射和出射的磁振荡模式来推断边界态的信息(基于能量-动量守恒原理),如图4(b)所示。对磁性系统中拓扑相的基础研究不但能揭示和理解这些有趣的拓扑物理,同时还能为将来设计受拓扑保护的自旋电子器件提供重要的参考和建议。该综述文章能为更好的设计基于磁振子和磁孤子的拓扑电子器件找准方向和理清思路。
该项工作得到了国家自然科学基金和中国博士后科学基金的资助。
编辑:lyn
-
导体和绝缘体实验及flash课件2010-01-27 1975
-
科学家在拓扑激子绝缘体相研究取得突破性进展2018-01-21 2602
-
2019年将迎拓扑材料“寒武纪”?NaNature同天3篇拓扑突破,中国团队“承包”2篇2019-03-12 5352
-
维尔茨堡大学获得首次成功地为拓扑绝缘体构建出量子点接触2019-10-30 3387
-
为什么在绝缘体中,光子会受到“拓扑保护”2020-06-04 6090
-
日本大阪大学的科学家利用光子拓扑绝缘体的概念制造了一种新型芯片?2020-08-13 2946
-
由拓扑绝缘体边界构成的“环形谐振器”及“波导-环形谐振器”耦合系统2021-01-14 4323
-
首次在零磁场下实现了量子反常霍尔绝缘体的陈数调控2021-01-15 2801
-
什么是拓扑绝缘体,它有没有可能替代硅2021-06-25 2296
-
拓扑绝缘体材料有望成为硅替代品?2021-06-27 3732
-
探讨一下2D和3D拓扑绝缘体2022-11-23 4292
-
基于外尔半金属的光场控制技术2023-01-31 384
-
微带线兼容的新型拓扑绝缘体结构:助力拓扑器件工程化2023-06-25 1534
-
一文详解绝缘体上硅技术2025-07-28 1953
-
高压放大器:弹性拓扑绝缘体弹性波技术研究的关键技术应用2025-08-12 570
全部0条评论

快来发表一下你的评论吧 !

