浅谈运算放大电路是如何表征噪声

即使是考虑到运放所有的已知及未知阻抗负载，运算放大器的输出中始终含有无法基于输入信号和完全已知的闭环传递函数进行预测的信号。这种不确定信号被称为噪声。

导致噪声产生的因素可能是放大器电路本身，可能是其反馈环路中使用的元件，也可能是电源；噪声也可能从附近（或较远的地方）的噪声源藕合或感应至输入、输出、地回路或测量电路之中的。

无疑，我们对噪声的关注程度取决于两点:

电路在目标频段所要达到的分辨率;

避免噪声转移至非直接相关频段。

由于运算放大器多用作前置放大器和高精度信号处理器，运算放大器电路的精度日益受到关注。所以今天我们就谈谈【噪声与运算放大器电路】。

从噪声角度来看，运算放大器具有独特的优势，完全适用于低压和高精度电路，因为:

可以选择特定的放大器传递函数，使其仅允许目标频段通过。

可以从具有不同噪声特性的众多型号中选择适应具体需要的放大器，以便在目标频段内获得近乎理想的特性。

如果噪声源已知且经过正确评估，则可预测各种放大器电路的噪声情况并达到足够的精度，从而为初步的手工设计提供依据，并具有一定的成功验证的可能性。

基本模型一一电压噪声与电流噪声

可将差分运算放大器视为理想的无噪声放大器，其噪声电流源位于各输入引脚与共模地之间，噪声电压源实际与某一侧输入引脚串联。该模型与失调分析2中用到的EOS一Ibias模型非常类似，这不足为奇，因为可将EOS和Ibias视为直流噪声源，可按时间、温度等参数进行调制。

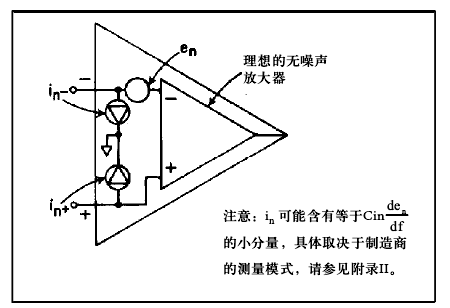
图1.电压与电流噪声模型

在多数实际应用中，可将噪声电压源和噪声电流源视为彼此独立的。如果暂时忽略电路和放大器的动态范围因素，就如EOS和Ibias一样，噪声的瞬时电压分量可通过低阻抗、高增益电路进行测量(图2)，而瞬时电流分量则可在一个很大(理想地“无噪声的”)电阻中进行测量。如果en与in之间无交互作用，则噪声电压测量输出将与(1 + R2/R1)成比例，而噪声电流测量输出则仅与R2成比例。

请注意，这两类噪声的瞬时和(出现于放大器输出端)为

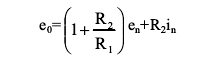
且在以下等式成立时，en和in的相对噪声贡献相等

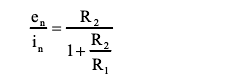
即条件为 : R2和R1的并联等于en与in之比。当阻抗水平高于en/in时，电流噪声占据主导。en和in均方根值之比有时被称为放大器在既定带宽下的“特征噪声电阻”，在选择与既定阻抗相匹配的放大器时可当作实用的品质因素，反之亦然。

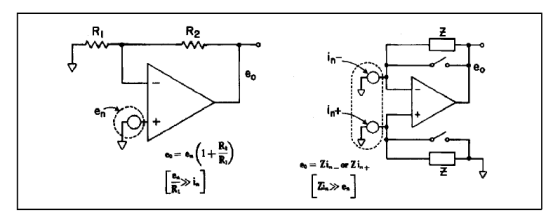
图2.  en和in的基本测量法

（窄带和点噪声测量中需使用滤波器）

在已知电压和阻抗的情况下，可将从外部源藕合至放大器输入引脚的噪声视为附加性的电压信号，或当这种信号的产生取决于放大器的某种测量方式时，也可视为附加性电流信号，简示为图3。

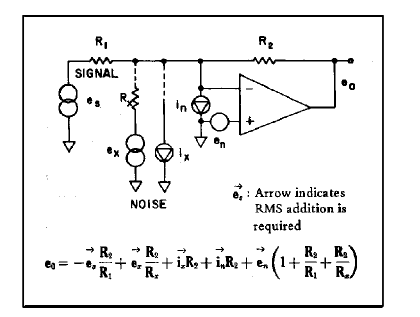
图3.内部和外部噪声源的贡献

噪声增益与信号增益

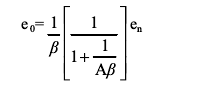
图4所示为一种反相放大器的基本反馈模型，其中含有数个阻性输入引脚。对于较大的环路增益值(Aβ），电压噪声的噪声增益实际为1/β。

图4.电压与电流噪声模型

如果Aβ不是远高于单位增益，则可使用以下更精确的表达式

相对应的电流噪声表达式为

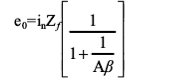
需要注意的是，对于无源反馈元件，1/β不会小于单位增益值，而且对于任意输入信号，该值也大于闭环增益。因此，即使信号增益小于单位增益，或者信号带宽较窄，但en的总频谱将出现在输出端，其值至少等于单位增益。

同时需要注意，一般情况下，当A和β均为动态表达式时，如果环路增益的相移一定程度上高于900，则放大器在接近Aβ=1时的频率范围处于欠阻尼状态，则该频率下的噪声增益的峰值可能高于单位增益很多，尽管信号增益在较低的频率时就会平滑滚降。图5为一种简单明了、易于理解的示例。

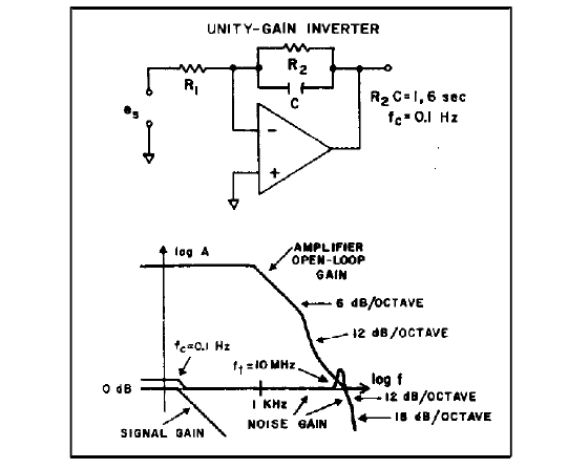
图 5.噪声带宽与信号带宽

如何表征噪声

周期性重复噪声可基于重现率、波形和幅度进行描写（如斩波器噪声）。不规则噪声则只能通过其波形和幅度进行描写，因为其变化无规律可言（在某种程度上来说，爆米花噪声属于此类）。无重复性波形的非周期性噪声一般通过其统计特性进行描述：均方根值、峰值和频率成分。

均方根值。多数随机噪声都存在以下特性:如果求平均值间隔较长，结果得到的均方根值具有较大的可重复性。因此，以均值法基于较长间隔求得的目标带宽均方根值，是确定这类随机噪声特性行之有效的方式。目前为止，这是厂商和客户都比较接受的估计噪声各因素的最简便方式。电压均方根值定义如下

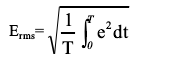
其中

Erms=均方根电压值

T=观测时间间隔

e=瞬时噪声电压

其中参数替换为瞬时电流值 i，则得到 Irms，即均方根电流值。进行均方根测量时，必须使用“真均方根”计量仪，也可将交流平均值(正弦波均方根校准型计量仪)的读数乘以因数1.13。

峰值。噪声也可表征为任意间隔观察到的最大正幅度与最大负幅度之差。在某些应用中，当峰峰值噪声可能限制系统性能时，可能需要采用峰峰测量法。

然而，从实用角度来看，由于噪声幅度分布呈高斯分布，因此最高噪声幅度的概率最低(但不为零)，难以重复测得峰峰值噪声。由于均方根值容易重复测得，而且是噪声数据公认的、最常用的表示方式，因此可利用下表估算在给定均方根的情况下，超过各种峰值的概率。

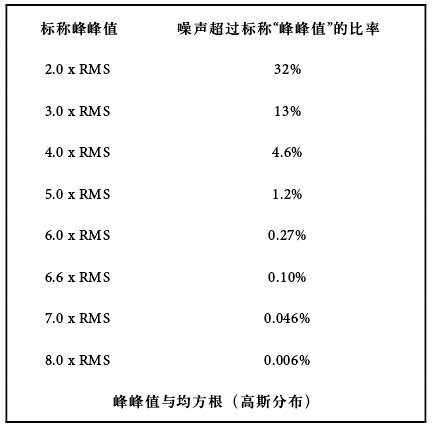
一般观测到的峰峰噪声值在3 x RMS与8 x RMS之间，取决于观测者的耐心及可用数据量。在较高的强度下才能观测到示波器的踪迹，然而由于大量平均求值运算是在低强度完成，此时将产生一个较为接近均方根值的结果。另外，市场上用于自动测量这类参数的峰值幅度分布分析仪也日益增多。

干扰噪声与固有噪声

既定电路的噪声可分为两个基本类别，即干扰噪声(指自电路外部拾取的噪声)和固有噪声(指电路内部产生的噪声)。

干扰噪声可能具有周期性，可能不规则重复，也可能完全随机，通过以下预防措施，往往可以大幅减少(或防止)这类噪声。比如，采取预防措施针对由电源线频率和谐波、无线电广播站、机械开关电弧以及阻性电路中开关带来的电流或电压尖峰等所引起的电磁干扰进行改善。这类预防措施包括滤波、去藕、对引线和元件进行静电和电磁屏蔽、使用防护电位、消除地环路、对引线和元件位置方向重新排布、在继电线圈中使用阻尼二极管、尽可能选用低电路阻抗、低噪型电源和基准源等。振动引发的干扰噪声可通过机械设计改善。图6中的表格列出了部分干扰噪声源、其典型值及处理方式。

图6.典型的干扰噪声源

然而，即使所有干扰噪声均得到消除，仍然存在固有噪声。固有噪声通常本质上属于随机噪声，多出现在电阻和半导体元件中，如晶体管和二极管等。（非随机固有噪声的一个例子是斩波器稳压型放大器中的斩波器噪声。）电阻元件中产生的随机噪声被称为约翰逊噪声（也称热噪声）。半导体元件中产生的随机噪声可能属于以下三类之一：肖特基噪声(或称散粒噪声)、闪烁噪声(1/f噪声)和爆米花噪声。

编辑：jq