硬件Kalman滤波器的航拍云台姿态如何获取

0 引言

航空摄影（Aerial Photography）又称航拍，是指在飞机或其他航空飞行器上利用航空摄影机摄取地面景物相片的技术。目前，航空摄影应用广泛，是获取地理信息的主要手段[1-2]。在航空摄影中，存在着一个难题需要解决：飞机在飞行摄影时会受到本机和气流等的影响，从而产生机体振动，相机的姿态角也会随着改变，相机姿态时刻改变就会给高精度拍摄带来困难。所以为提高航拍质量，必须对相机姿态进行校正[3]。

校正的前提是获取相机姿态，所以惯性测量元件必不可少，但是单一的惯性测量元件无法给出准确的姿态角，需要对多个惯性测量元件的数据进行数据融合。使用比较普遍的惯性测量元件的组合是加速度计和陀螺仪。它们输出的数据各有优缺点，可以使用Kalman滤波对其进行数据融合以得到准确的姿态角[4-5]。

现有的实现Kalman滤波的方式主要有两种：PC机和DSP，两者都存在着系统性能和成本不能兼顾的问题。而FPGA却可以很好地解决这个问题。本文主要讲述的便是用FPGA实现Kalman滤波来获取准确的相机姿态。

1 坐标模型

在进行航拍作业时，相机搭载在云台上，云台和飞机是一体的，当相机拍摄地面照片时，相机拍摄方向应与地面垂直，如图1所示。

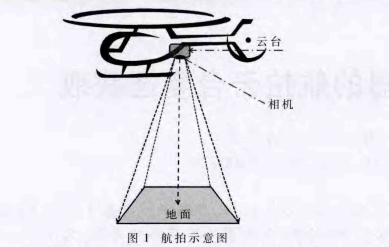
为获取相机姿态，首先以相机为原点，建立坐标系，如图2所示。其中，XY平面与地面平行，Z轴垂直于地面，Y轴方向为飞机飞行方向。

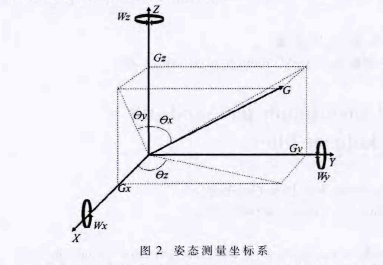
将加速度计固定在相机上，当相机姿态发生改变时，加速度的3个敏感轴便可以输出在其相应方向产生的重力分量信号，如图2中的Gx，Gy，Gz所示。陀螺仪是一种角速度传感器，它可以输出对应轴上的瞬时角速度，如图2中的Wx，Wy，Wz所示。

根据以上坐标系，可以得到姿态角θx，θy，θz（分别代表着俯仰角、横滚角、偏航角），如式1所示，其中ΔT为采样时间，Δθ为采样时间内的姿态角变化。

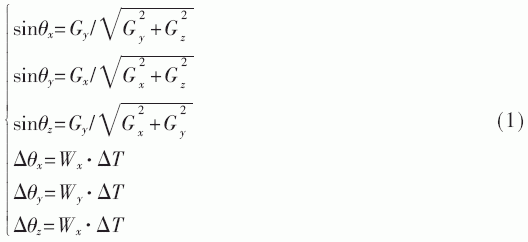
可见，由加速度计或者陀螺仪都可以初步得到姿态角，但是无论是加速度计还是陀螺仪，它们输出的原始数据都存在着固有缺陷：当相机处于变速运动状态时，加速度计的输出并不是重力加速度，而是重力加速度和其自身加速度的矢量和。陀螺仪是通过对角速度积分得到姿态角，随着时间的推移，姿态角的误差会越来越大。所以单一的加速度计或者陀螺仪都无法获得正确的姿态角，必须对两者进行数据融合。

2 Kalman滤波模型的建立

Kalman滤波是在时域内以信号的一、二阶统计特性已知为前提、以均方误差极小为判据，能自动跟踪信号统计性质的非平稳变化，具有递归性质的一种算法[5]。Kalman滤波的状态方程和预测方程如式(2)所示：

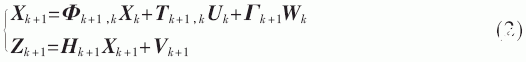
其中，Xk+1为系统的状态向量，Φk+1，k为状态转移矩阵，Tk+1，k为控制系数矩阵，Uk为系统控制输入，Γk+1为噪声系数矩阵，Wk为系统的过程噪声序列，Zk+1为系统的观测序列，Hk+1为观测矩阵，Vk+1为观测噪声序列。

使用陀螺仪数据建立线性模型，如式(3)所示：

其中，θk为飞行姿态角，βk为陀螺仪输出的误差，Uk是陀螺仪输出的角速度数据，ΔT是采样时间间隔。因为陀螺仪输出的误差整体来看变化不大，可认为βk+1=βk。因Wk对系统影响甚小，这里规定Wk=0。

由以上建立状态矩阵方程，如式(4)所示：

 

陀螺仪和加速度计测量姿态角时各有优缺点，为获得比较可靠的姿态角数据，必须对两者的数据优势互补。以上算法用加速度计数据得到不同阶段的测量噪声协方差，并带入解算过程中，大大减少了姿态角的测量误差。

3 Kalman硬件实现

目前Kalman滤波器的实现方式主要有PC机和DSP两种方式，PC机可以同时满足计算精度和实时性的要求，但是PC机体积大、质量重、成本高；DSP实现的Kalman滤波器虽然体积小，质量轻，但是因其指令顺序执行的CPU架构，在系统复杂时无法满足系统的实时性要求[6-7]。

因此，Kalman滤波器在工程应用中的实现遇到了系统体积、重量、成本与系统精度、速度等性能不能兼顾的问题。FPGA是解决这一问题的有效途径，FPGA具有极高并行度的信号处理能力、高度的灵活性、现场可以编程、较短的开发周期和较低的成本等优势，在数字信号处理领域已经得到广泛的应用[8]。

本系统使用的FPGA芯片是Altera公司Cyclone II系列中的EP2C35F672C6，它共有33 216个逻辑单元、483 840个存储单元、70个乘法器单元（9 bit）。虽然Altera公司提供了很多功能强大的IP核，其中就包括加减乘除单精度浮点数运算，但是提供的IP核占用资源过多，所以使用自己编写的运算模块。下面以除法模块为例说明浮点数运算的硬件实现。

3.1 浮点数除法模块

根据IEEE754标准，单精度浮点数的格式如图2所示。

通常可用式(11)表示一个单精度浮点数：

从式(12)中可以看到，符号位和阶码的运算比较简单，尾数的运算较为复杂。

设被除数为a，除数为b，第i次的商为qi，第i次得到的临时余数为mi，令m0=a，则有式(13)：

这样一直进行23次运算便可以获得全部的qi，23位qi按先后顺序组合起来便是尾数运算的结果。

除法模块资源使用情况如图3所示，只使用了1%的逻辑单元，相比较于IP核的实现方式，大大减少了使用资源。

再用ModelSim仿真观察除法模块运算速度，结果如图4所示。x1，x2是除数和被除数，y是商，isdone是标志信号，当完成一次除法运算后产生一个正脉冲。

由图4可以看到，除法模块运算一次共使用了25个CLK周期，完全可以满足运算要求。

3.2 Kalman硬件模块

以第2节中建立的卡尔曼滤波模型搭建硬件模块，硬件模块的结构如图5所示。其中，

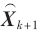
为整个Kalman滤波的结果矩阵，包括横滚角、俯仰角、偏航角。

Kalman硬件模块使用资源情况如图6所示。可见，一共使用了45%的逻辑单元。虽然占用资源非常多，但是45%的资源使用还是可以接受的。

利用Multisim仿真，查看此Kalman硬件模块的运行速度，结果如图7所示。

q1、q2、q3是Kalman滤波解算一次后的3个偏转角（横滚角、俯仰角、航向角），q1st、q2st、q3st是解算一次完成后产生的负脉冲信号。从仿真结果来看，在仿真频率为100 MHz情况下，Kalman解算一次需要的时间是1 ms，可见用FPGA来实现Kalman滤波速度是很快的。

4 实验结果

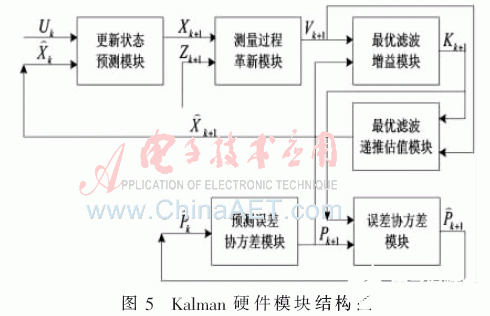
为检验Kalman滤波硬件模块实际效果，设计了一次模拟实验：将云台置于振动环境中，改变云台姿态角，观察未经滤波处理和经过滤波处理的姿态角。

实验中使用MPU6050作为系统的姿态传感器，MPU-6050是一款整合了3轴陀螺仪、3轴加速度计的6轴运动处理组件，相比较于多组件方案，免除了组合陀螺仪与加速度计时之轴间差的问题，减少了大量的包装空间。

设置采样频率为1 kHz，以横滚角为示例，实验结果如图8所示。

滤波前的横滚角由三轴加速度和式（1）得到，可以看到明显的噪声和毛刺。经过Kalman滤波后，大部分的噪声和毛刺都被去除掉了，而且通过滤波前后的横坐标对比可以看到此滤波模块有着很好的实时性能。

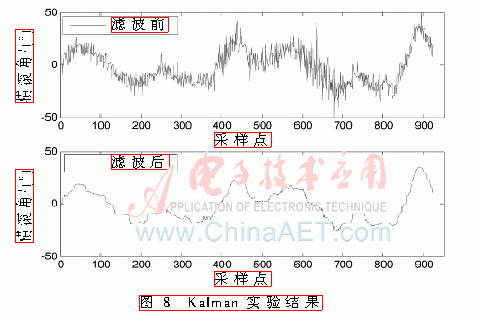
观察滤波结果与真实值之间的误差，如图9所示。从图中可以看到，滤波误差控制在-1.5°～1.5°范围内。可以满足航拍系统的精度要求。

5 结论

实验证明，本文所介绍的硬件Kalman滤波器适用于航拍相机平台的姿态获取。基于FPGA的硬件架构具有灵活的可移植特性和优良的抗干扰能力，相比较于DSP和PC机的实现方式，它在保证航拍系统的精度要求的前提下解决了性能和成本不能兼顾的问题，因此它具有更广泛的应用性和实际工程意义。

参考文献

[1] 刘先林，段福洲，宫辉力.航空摄影科技发展成就与未来展望[J].前沿科学，2007，3(3)：10-14.

[2] 张祖勋.数字摄影测量发展与展望[J].地理信息世界，2004，2(3)：1-5.

[3] 高同跃，丁卫，高新闻，等.机载惯性稳定云台系统的研究[J].2010，18(2)：344-347.

[4] 卞鸿巍,李安,覃方君，等.现代信息融合技术在组合导航中的应用[M].北京：国防工业出版社，2010.

[5] 付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用(第二版)[M].北京：科学出版社，2010.

[6] 谢鑫，郭美凤，周斌.基于双DSP和FPGA的高性能导航计算机设计[J].微计算机信息，2009(3)：1-2，60.

[7] 张冲，吴秋平.基于PC104和DSP的分布式导航计算机设计[J].微计算机信息，2010(8)：27-29.

[8] 米月琴，黄军荣.基于FPGA的Kalman滤波器的设计[J].电子科技，2010，23(2)：52-55.

编辑：jq