浅谈参数约束关系的工业相机的线性标定法

摘  要： 提出了一种基于参数约束关系的工业相机的线性标定法，该方法充分考虑了摄像机标定参数之间的约束关系，利用单位正交矩阵的6个约束关系，使标定误差按参数之间的约束关系进行分配。该方法既避免了摄像机非线性标定所需优化算法的繁琐和不稳定，亦解决了其他线性标定法中摄像机内外部参数分解误差大的问题，是一种简单、高效、实用的摄像机标定算法。

视觉检测由于具有非接触、测量速度快、信息量大等优点而被广泛应用于质量检测[1-2]、尺寸检测[3-5]以及方位检测[6-8]等诸多工业检测领域[9]。其中，视觉检测的一个基本任务就是通过工业相机获取的二维图像信息精确地计算出空间物体的三维几何信息，而实现这一过程的前提和基础是摄像机标定[10-12]。

摄像机标定就是确定摄像机的位置、属性参数（称为摄像机内外部参数），以便于确定世界坐标系中物理点与其在图像坐标系中所成的像点之间的对应关系[13]。精确标定摄像机内外部参数不仅可以提高视觉检测任务的可靠性，而且还可以提高视觉检测任务的精度；同时，标定的实时性可以更好地满足工业现场检测应用的需要。

目前摄像机标定方法很多，按其求解算法大致可以分为线性标定法、非线性标定法以及两步法[14]。本文提出了一种用于工业视觉检测应用的简单的摄像机标定方法。该方法是一种全线性标定方法，只利用线性方程和矩阵计算，分解出摄像机内外部参数，由于在进行参数分解时充分考虑了摄像机标定参数之间的约束关系，实现了标定误差按参数之间的约束关系进行分配，因而该算法精度高、速度快。

1 摄像机模型及标定参数

1.1 针孔成像模型

理想的摄像机成像模型是针孔模型，由于摄像机光学系统的加工误差和装配误差，摄像机实际成像并不完全满足针孔成像，即摄像机实际成像与理想成像之间存在着光学畸变误差[15]。由于针孔成像原理简单，再加之现代光电技术的发展，摄像机成像的畸变误差越来越小，成像质量越来越高，因此在针孔成像模型的基础上，只要适当地考虑一些镜头的畸变因素，就能满足多数的应用需求。因此，本文的成像模型采用针孔模型，如图1所示。

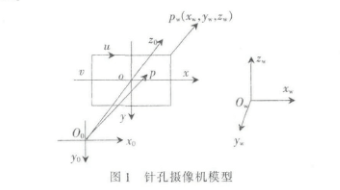
该模型共有4个坐标系，分别为：

（1）世界坐标系owxwywzw：是由用户任意定义的三维空间坐标系，（xw，yw，zw）表示物点P在世界坐标系下的三维坐标。

（2）摄像机坐标系o0x0y0z0：是以镜头光学中心为原点，z0轴平行于摄像机光轴的坐标系。世界坐标系与摄像机坐标系的变换可以用旋转矩阵R和平移向量T来描述：

x0y0z0=Rxwywzw+T（1）

其中，R=r11  r12  r13r21  r22  r23r31  r32  r33，T=txtytz。

（3）图像物理坐标系oxy：原点位于摄像机光轴与图像平面的交点，x、y轴分别与x0、y0轴平行。摄像机坐标系与图像物理坐标系的变换为：

xy1=f  0  00  f  00  0  1x0y0z0（2）

（4）图像像素坐标系ofuv：原点of位于CCD图像平面的左上角，单位是像素，设图像平面中心坐标（即图像物理坐标系的原点o在图像像素坐标系中的坐标）为（u0，v0），u和v分别表示像素所在的列和行。图像物理坐标系与图像像素坐标系的变换为：

uv1=1/dx   0   u0 0   1/dx  v0 0    0   1xy1（3）

从世界坐标系owxwywzw到图像像素坐标系总的变换为：

z0uv1=?琢x  0  u0  00   ?琢y    v0  00  0  1  0R  T0  1 xwywzw1=Mxwywzw1（4）

1.2 需要标定的参数

（1）外部参数：包括R和T，共12个，但因R为单位正交矩阵，必须满足6个正交约束条件，故实际上只有6个外部参数需要标定。

（2）内部参数：包括?琢x、?琢y、u0、v0 4个。其中，?琢x=f/dx，?琢y=f/dy、dx、dy分别为一个像素在x、y方向上的物理尺寸。

2 参数标定

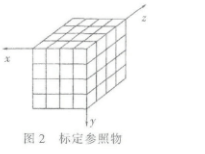
做一个特制的标定参照物如图2所示，摄像机获取该参照物图像，用特征点提取算法计算参照物上每一个标定点的图像像素坐标u、v，世界坐标系可选标定参照物的物体坐标系。已知标定参照物上标定点的世界坐标及其对应的图像像素坐标，就可以求出摄像机投影变换矩阵M。

将式（4）改写为：

z0uv1=Mxwywzw1=m11  m12  m13  m14m21  m22  m23  m24m31  m32  m33  m34xwywzw1（5）

整理消去z0后，可得到如下两个线性方程：

m11xw+m12yw+m13zw+m14-um31xw-um32yw-um33zw=um34

m21xw+m22yw+m23zw+m24-vm31xw-vm32yw-vm33zw=vm34（6）

对每一个标定点都有式（6）所示的两个方程。若采用n≥6个点，就可以得到2n个关于mij的线性方程，用最小二乘法可以计算出投影变换矩阵M的系数。

xw1 yw1 zw1 1  0 0 0 0 -u1xw1 -u1yw1 -u1zw1 0  0 0  0 xw1 yw1 zw1 1 -v1xw1 -v1yw1 -v1zw1 … … … … … … … …  …    …   …xwn ywn zwn 1  0 0 0 0 -unxwn -unywn -unzwn 0  0 0  0 xwn ywn zwn 1 -vnxwn -vnywn -vnzwnm=m34u1m34v1 …m34unm34vn（7）

其中，m=[m11 m12 m13 m14 m21 m22 m23 m24 m31 m32 m33]T。

变换矩阵M由4个内部参数和6个外部参数（3个独立旋转矩阵参数，3个独立平移参数）组成，即M矩阵应由10个独立的变量确定。但M为3×4的矩阵，共有12个参数。对于式（5）来说，M乘以任何不为零的常数都不会影响（xw，yw，zw）与（u，v）的关系，所以可以指定m34=1，故M矩阵由11个参数确定。可见这11个参数并非相互独立，存在着变量之间的约束关系，但用式（7）求解这些参数时，并没有考虑这些参数之间的约束关系，因此在数据存在误差的情况下，计算结果肯定是有误差的，且误差没有按照参数之间的约束关系进行分配，特别是在分解内外部参数时，误差显得尤为突出。

为此，本文提出一种基于参数约束关系的线性标定法，通过考虑参数之间的约束关系来提高参数标定的精度。具体计算过程如下：令式（7）两边同除以m34，变换后公式缩写为Kd=U。其中，K为式（7）左边2n×11的矩阵；d=[d1 d2 d3 d4 d5 d6 d7 d8 d9 d10 d11]T，d1，…，d11分别表示；U=[u1 v1 … un vn]T。然后利用最小二乘法求解矩阵d为：

d=（KTK）-1KTU（8）

由式（4）、（5）可得：

?琢xR1T+u0R3T  ?琢xtx+u0tz?琢yR2T+v0R3T  ?琢yty+v0tz    R3T        tz=M1T  m14M2T  m14M3T  m14（9）

其中，M1T ，M2T ，M3T分别是矩阵M的第1、2、3行的前3个元素；R1=[r11 r12 r13]T，R2=[r21 r22 r23]T，R3=[r31 r32 r33]T，R=R1T R2TR3T，并且它们之间满足如下关系：

‖R1‖2=r112+r122+r132=1（10）

‖R2‖2=r212+r222+r232=1（11）

‖R3‖2=r312+r322+r332=1（12）

R1TR2=r11r21+r12r22+r13r23=0（13）

R2TR3=r21r31+r22r32+r23r33=0（14）

R3TR1=r11r31+r12r12+r23r33=0（15）

由式（9）可以看出M3=R3，所以‖M3‖2=1，即（d92+d102+d112）m342=1，则可以求出：

m34=16）

则m11=d1m34，m12=d2m34，m13=d3m34，m14=d4m34，m21=d5m34，m22=d6m34，

m23=d7m34，m24=d8m34，m31=d9m34，m32=d10m34，m33=d11m34。

变换矩阵M的各个参数求解如下：

R3=M3tz=m34u0=（?琢xR1T+u0R3T）R3=M1TM3v0=（?琢yR2T+v0R3T）R3=M2TM3?琢x=|M1×M3|?琢y=|M2×M3|R1=

综上所述，由6个以上点就可以计算出变换矩阵M，并且在求解内外参数时利用了单位矩阵的6个约束关系，对摄像机内外参数进行分配，即便数据存在误差，误差也能按照各参数之间的约束关系分配，从而提高了标定精度。

本文基于理想的摄像机小孔模型，对目前摄像机的线性标定法进行了分析。针对以往线性标定中参数并非相互独立而无法准确计算出摄像机内外参数的问题，提出了一种基于参数时间约束关系的线性标定法。该方法充分考虑了摄像机标定参数之间的约束关系，利用约束关系计算摄像机内外部参数，使数据误差能够按各参数之间的约束关系进行分配，从而可以提高摄像机标定的精度。

参考文献

[1] 王小鹏，刘志华，陈天宁.透明材料微小器件键合质量检测系统设计[J].光学精密工程，2013，21（1）：69-75.

[2] 蒋兴良，夏云峰，张志劲，等.基于优化Gabor滤波器的输电导线断股图像检测[J].电力系统自动化，2011，35（15）：78-83.

[3] 孙岩，张征宇，黄诗捷，等.风洞试验中模型迎角视觉测量技术研究[J].航空学报，2013，34（1）：66-69.

[4] 程朋乐.面向装配的微小型零件视觉检测技术[J].电子测量与仪器学报，2013，27（2）：151-155.

[5] 任子真，王保辉.塑料铆接缝隙图像检测系统的研究[J].微型机与应用，2013，32（3）：32-34.

[6] 吴俊君，胡国生.室内环境仿人机器人快速视觉定位算法[J].中山大学学报（自然科学版），2013，52（4）：7-13.

[7] 谭磊，王耀南，沈春生.输电线路除冰机器人障碍视觉检测识别算法[J].仪器仪表学报，2011，32（11）：2564-2570.

[8] 袁俊杰，何广平.基于视觉定位和力反馈的铝电解阳极炭碗清理系统[J].制造业自动化，2013，35（8）：137-141.

[9] 盛遵冰.机器视觉图像检测与定位系统关键技术研究[D].哈尔滨：哈尔滨工业大学，2009.

[10] SALVI J， ARMANGU X， BATLLE J. A comparative review of camera calibrating methods with accuracy evaluation[J]. Pattern Recognition， 2002，35（7）：1617-1635.

[11] 邱茂林，马颂德，李毅.计算机视觉中摄像机定标综述[J].自动化学报，2001，26（1）：43-55.

[12] 张曦，黄亮，徐洋，等.基于MATLAB中calibration toolbox的相机标定应用研究[J].微型机与应用，2011，30（14）：31-33.

[13] 张铖伟，王彪，徐贵力.摄像机标定方法研究[J].计算机技术与发展，2010，20（11）：174-179.

[14] 邹凤娇，苏显渝，李美菊.基于共面点的摄像机线性标定法[J].光电工程，2005，32（4）：70-74.

[15] WENG J， COHEN P ， HERNIOU M. Camera calibration with distortion models and accuracy evaluation[J]. Transactions on Pattern and Machine Intelligence， 1992，14 （10）：324.

编辑：jq