常见的动态规划题目

注：本文是BAT真题收录很值得大家花心思看完，看完会有收获。

前言

算法是面试大公司必考的项目，所以面试前准备好算法至关重要，今天整理的常见的动态规划题目，希望可以帮到大家。

要想学习其他绝世武功，要先打好基础。算法属于内功，则更为重要。

强盗抢劫

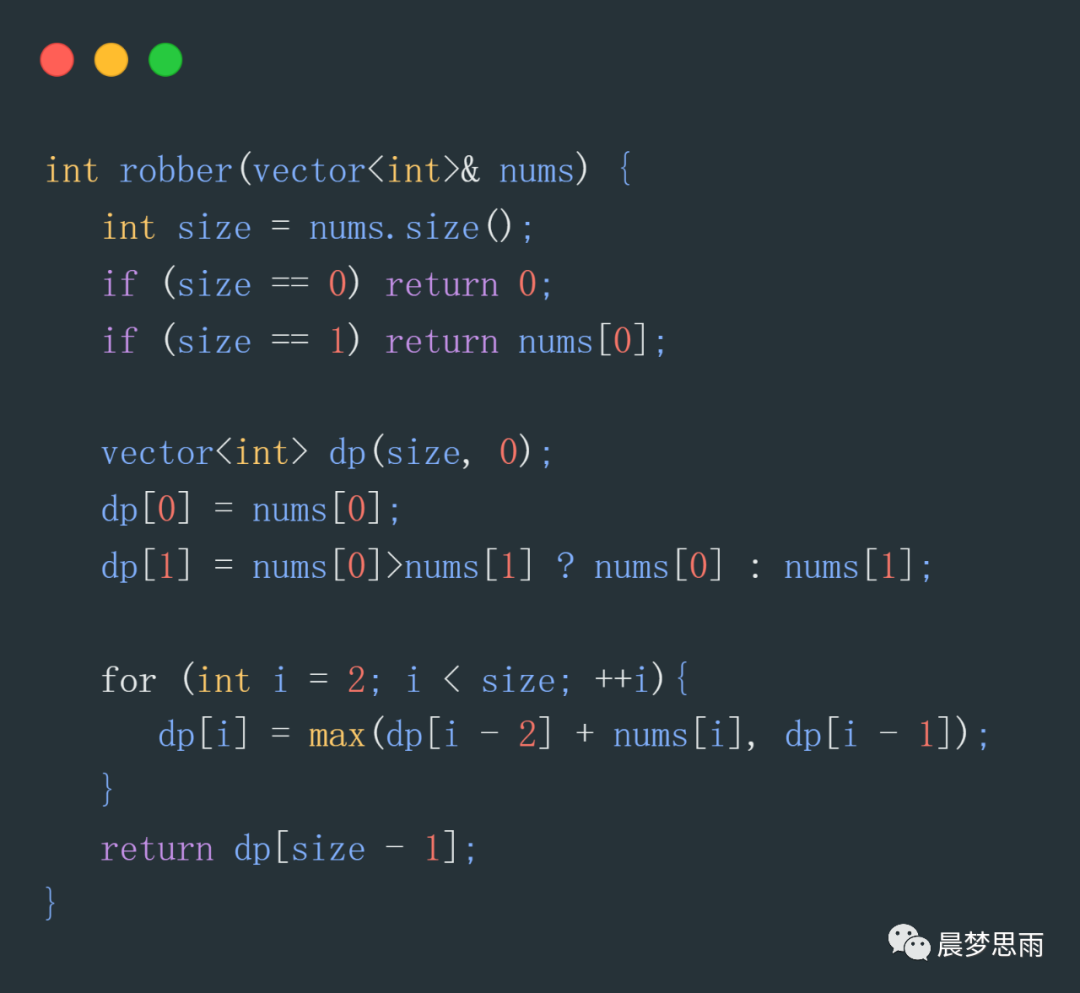
题目：强盗抢劫一排房间，每个房间都有钱，不能抢劫两个相邻的房间，要求抢的钱最多。数组如：[2,7,9,3,1]

思路：当输入房间数为0,1,2时，这个很好判断，当输入房间数字大于3时，就要用到动态规划了，方程是:

dp[i]是当抢到第i个数时，能抢到最大值，从局部最大值推到最终结果最大。

假如抢到第5个房间，那么第5个房间有二种情况，抢不和不被抢，因为只能隔房间。

如果抢到第4个房间，有个最大值；抢到第3个房间，有个最大值。

如果加上第3房间最大值，加上第5房间的最大值，大于抢到第4个房间时的最大时。那就抢3,5而不抢4，反而，就按抢4的策略。

这样从前往后推，最后的结果一定是最大的。

代码如下：

 

跳台阶

题目描述：有 N 阶楼梯，每次可上一阶或两阶，求有多少种上楼梯的方法

先来分析下这个问题：

当N=1时，这个很好理解，只能跨1步这一种了

当N=2时，你每次可以跨1步或2步，那就是走2步或走两个1步

当N=3时，因为你可以跨1步或2步，那你在台阶1或2都能行。要计算到台阶1有多少种走法，到台阶2有多少种走法，然后2种相加，依次逆推。

当N=4时，你在台阶2或3都能行，计算到台阶2有多少种走法，到台阶3有多少种走法，然后2者相加，依次逆推。

总结如下：你会发现，这是斐波拉切数列，使用递归出现重复计算问题，所以选择动态规划算法。

 

层数	公式	种数
1	f(1)=1	1
2	f(2)=2	2
3	f(3)=f(1)+f(2)	3
4	f(4)=f(2)+f(3)	5

 

第三层：3种（在第一层走2步或在第二层走1步）

第四层：5种（在第二层走2步或在第三层走1步）

i,j首先赋边界值，res保存i+j的值，每次前进，i,j,res的值都会被赋到前面结果。

上面的算法是底向上，递归相当于自顶向下，避免了重复计算。
 

矩形最小路径和

题目：
给定一个，包含非负整数的 m x n 网格。请找出一条，从左上角到右下角的路径。使得路径上，所有数字总和为最小，每次只能向下，或者向右移动一步。

输入:[[1,3,1],
      [1,5,1],
      [4,2,1]]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

先看动态方程：

 

i值	j值	dp方程
i>0	j=0	dp[i][0] = dp[i−1][0] + grid[i][0]
i=0	j>0	dp[0][j] = dp[0][j−1] + grid[0][j]
i>0	j>0	dp[i][j] = min(dp[i−1][j], dp[i][j−1]) + grid[i][j]

 

说明：因为 i=0 和 j=0 是临界条件，所以要先求出来。当 i>0 和 j>0 时，看如上数组，5 可以由上方3，或者左方 1 走过来。

当走5的时候，要选取上方3对应的dp，与左方1 对应的dp进行比较，选择较小值累加，这样走出来的才是最小值。最后推出，到右下角的最小值。

代码如下：

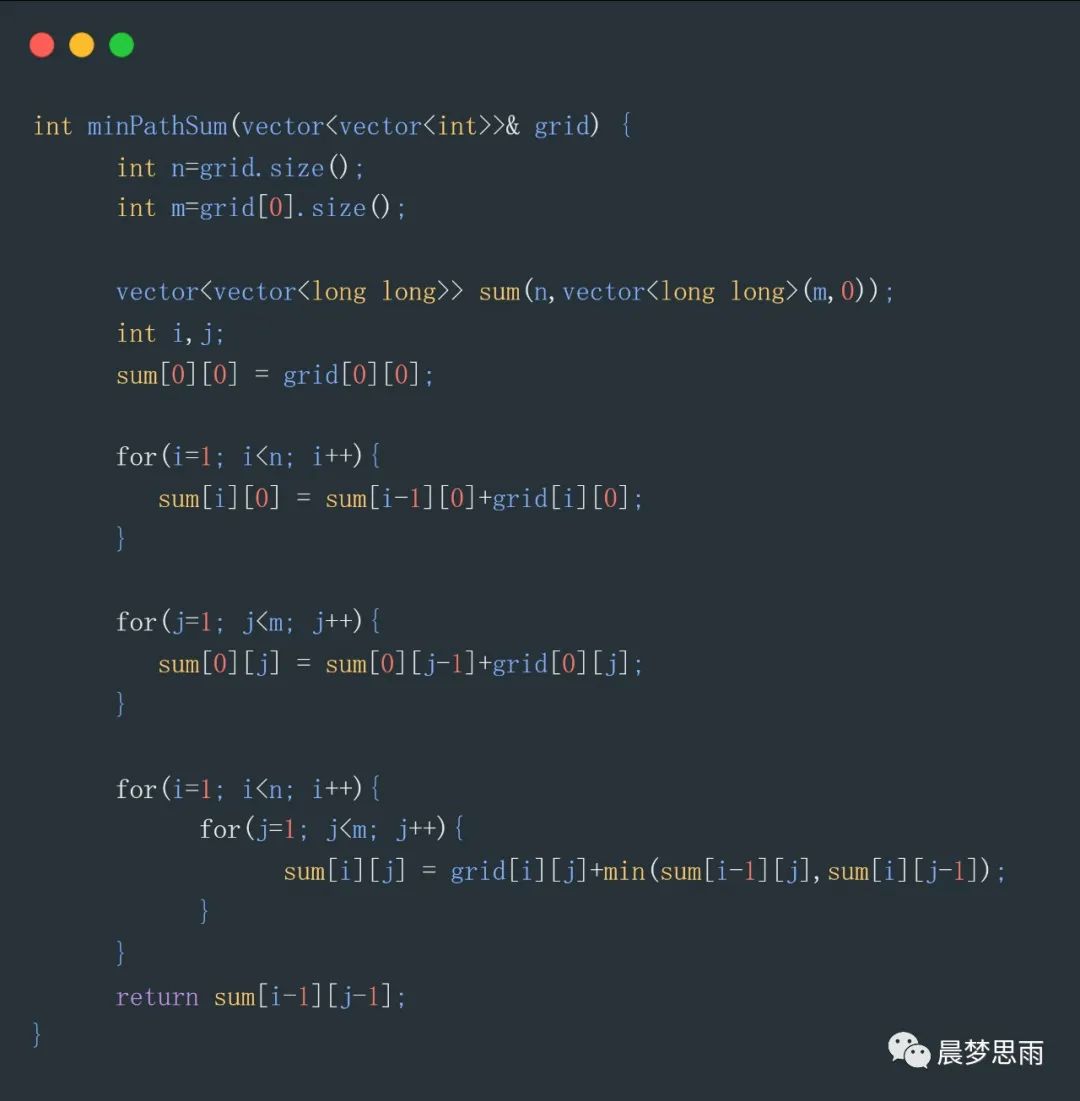
sum用来存储，从[0][0]到sum[i][j]路径的最小和，看看每次sum的变化，sum[1][1]=7意思是，从[0][0]到[1][1]路径最小和是7。

程序先把，第2行对应的sum都求出来，再把第2列对应的sum都求出来，最后求sum[2][2]就很容易了。

最后，sum[i-1][j-1]就是推出的最小值，上述代码就是dp方程的实现。
 

划分数组为两个相等的子集

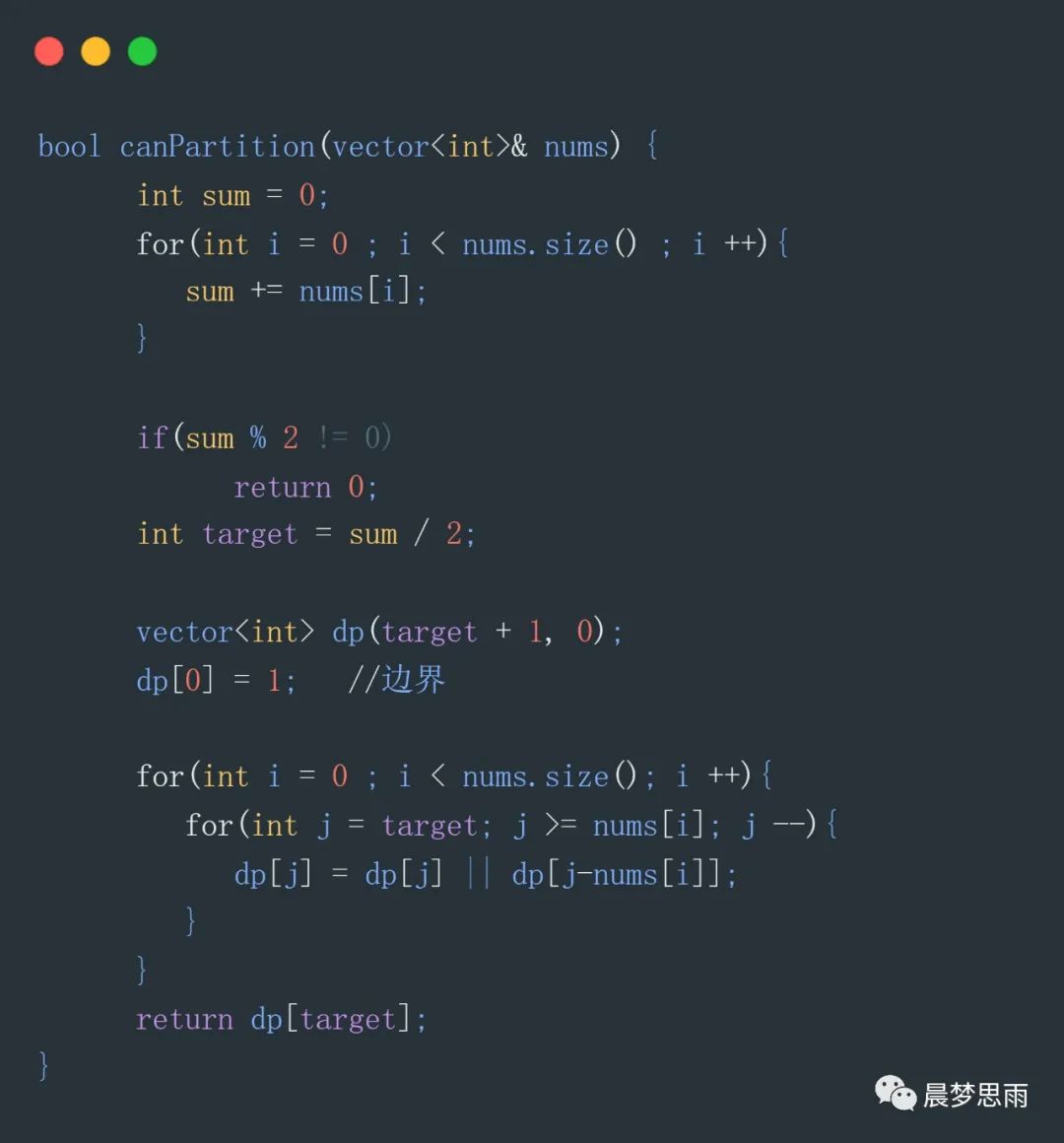
题目：输入：[1, 5, 11, 5]， 输出：[1, 5, 5]和[11]

思路是，相对数组中每个数求dp，最后就会找到dp[target]是否为true。

如果 dp[j - nums[i]] 为true的，说明可以组成 j-nums[i]这个数，再加上nums[i]，就可以组成数字j。

当j = target是同样道理，要想找到dp[target]为true，就找到数组中，几个值的和为target时，对应下标的dp值为true，这样反推dp[target]为true。

代码如下：

乘积最大连续子数组

题目：
输入一个整形数组，数组里有正数也有负数。数组中连续的一个，或多个整数组成一个子数组，每个子数组都有一个和。求所有子数组的和的最大值。

例如数组：arr[]={1, 2, 3, -2, 4, -3 } 最大子数组为 {1, 2, 3, -2, 4} 和为8。

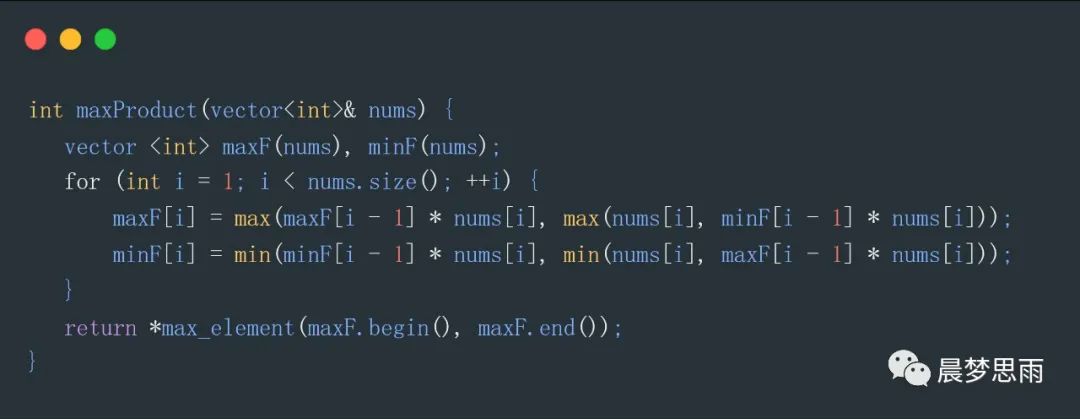
思路：fmax(i) 表示，以第 i 个元素结尾的，乘积最大子数组的乘积，fmin(i) 表示，以第 i 个元素结尾的，乘积最小子数组的乘积。

这里分为最大和最小是因为数组可能存在负数，最大值乘以负数变成较小值，最小值乘以一个负数也可能变成最大值。

比较方程是：当前数乘以上一个最大值，当前值，当前数乘以上一个最小值。这三者比较，其中的最大值，就是我们要的最大值。

同样，每次也要把最小值计算出来，方式同上。

代码如下：

等差递减区间的个数

题目：求一个数组中等差递减区间个数，等差数列必须是连续的。

例子：A = [1, 2, 3, 4]，个数为3，分别是: [1, 2, 3], [2, 3, 4] 

等差数列公式：

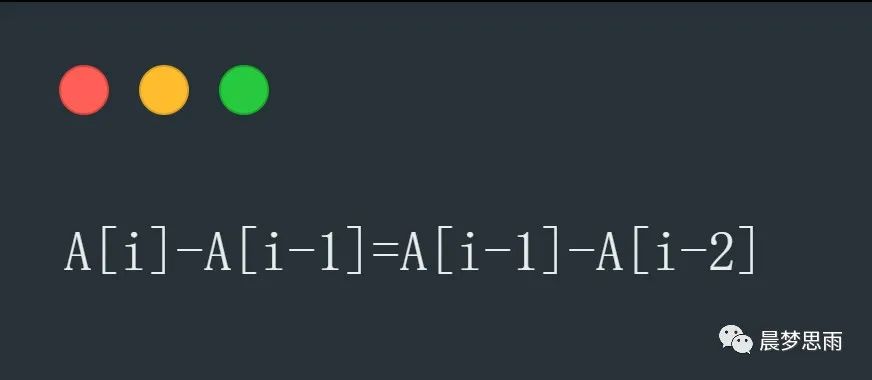
先看一个表：
 

 

数组	等差数列的数目	与上一组等差数列比较
1 2 3	1	1 - 0 = 1
1 2 3 4	3	3 - 1 = 2
1 2 3 4 5	6	6 - 3 = 3
1 2 3 4 5 6	10	10 - 6  = 4

 

其实仔细观察，发现这是一个斐波拉切数列，0,1….n-2数的求和，动态规划找到方程了，就发现非常简单了。

这就是规律，但需要自己去发现规律，有些题目咋看一脸懵逼，仔细看就会发现其中的规律。

dp[i] 表示到i位置时，子数组的个数。数组长度大于3。

下面看下代码：

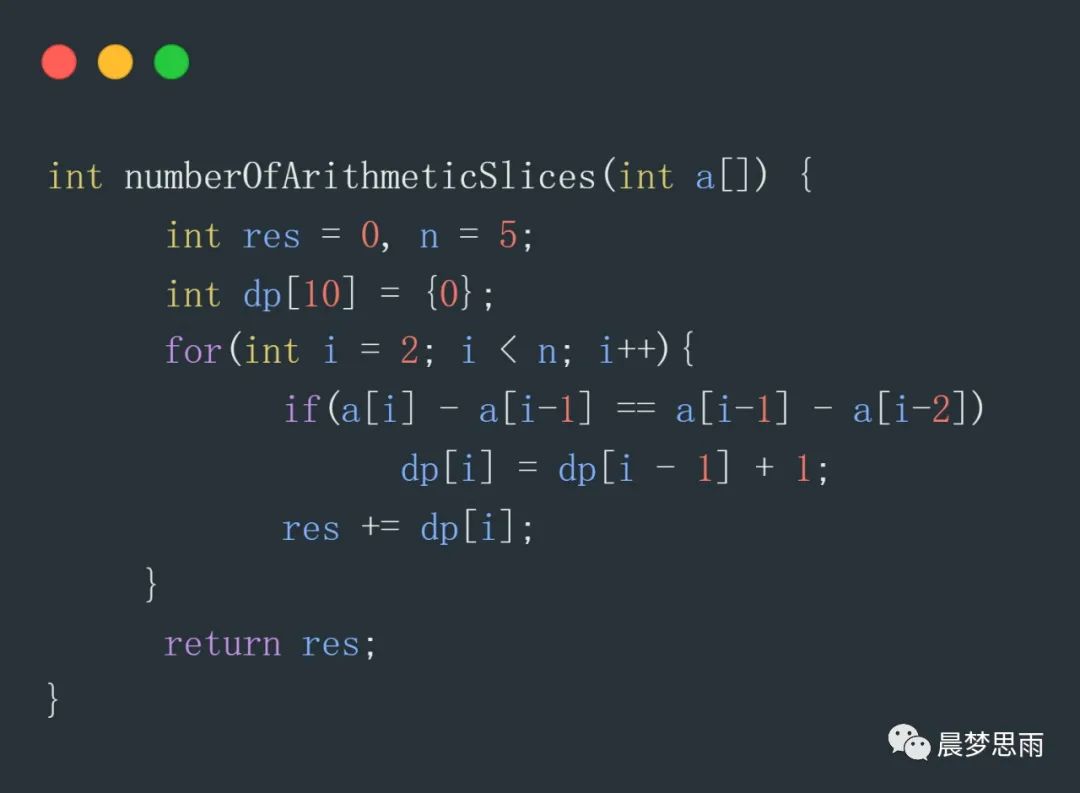
下面再看代码执行值的变化过程：

 

i值	子数组	dp[i]	res
i = 2	123	1	1
i = 3	123 234 1234	2	3
i = 4	123 234 1234 2345 12345	3	6
i = 5	123 234 1234 2345 12345 23456 123456	4	10

 

很明显，就是0,1….n-2数的求和。
 

最长回文子串

题目：求最长回文子串。输入: "babad"，输出: "bab"。注意: "aba" 也是一个有效答案。

dp[i][j]表示，字符s从下标i到下标j，是否为回文串。

如果bab是回文串，那么ababa也是回文串。因为，在两边增加了相同的数。同理，可以给出动态方程：

下面看下代码：
 

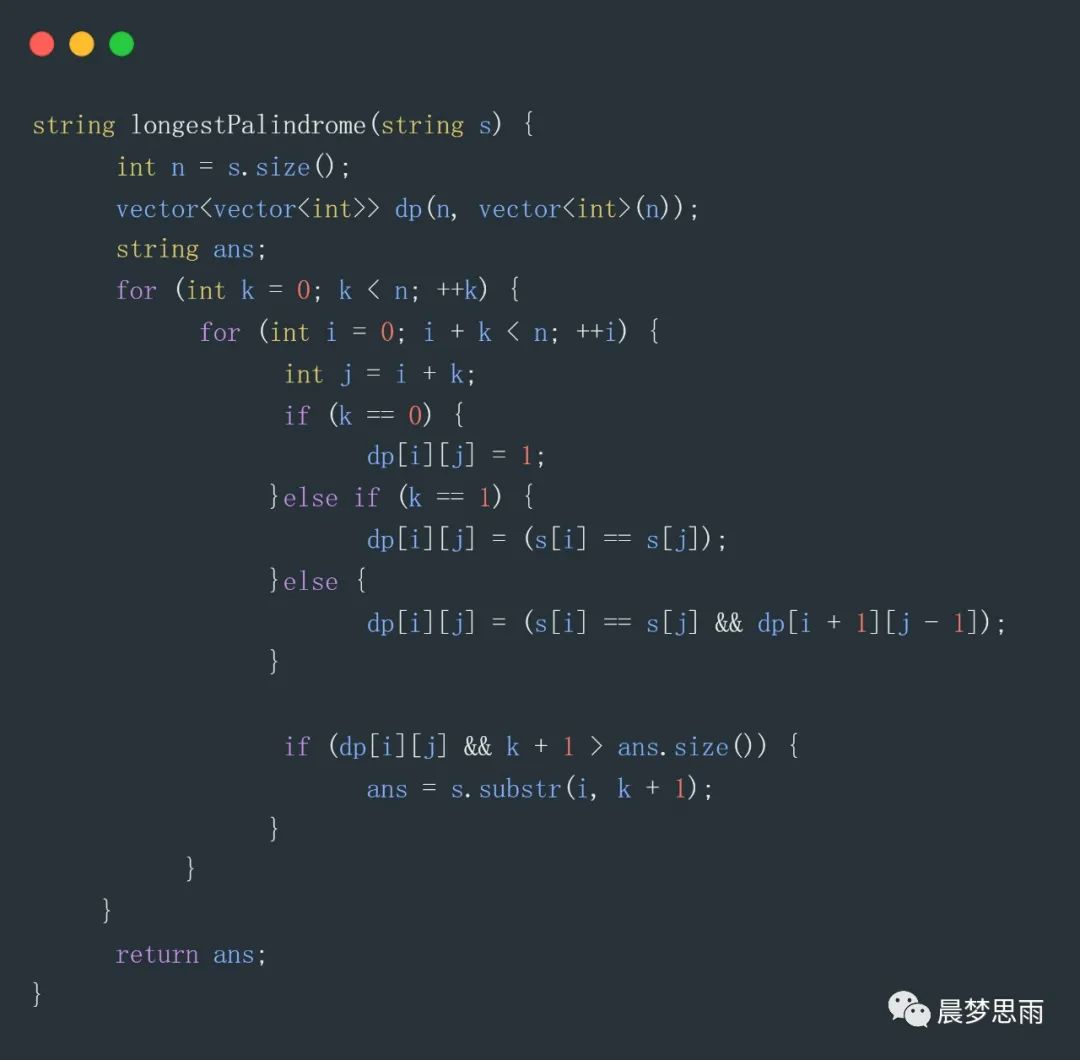
这段代码用利用了 dp[i + 1][j - 1]，其前面已经计算出来了。

当k = 4时，字符串最长，最后符合条件的回文子串最长。注意整个循环遍历的过程，用k最为两个下标的间距，然后遍历每种可能的结果，判断是否回文。

最长的子串最后判断，将符合条件的子串保存起来。动态规划方程推测极为重要。
 

最长递增子序列

求一个数组的最长自增子序列。

输入: [10,9,2,5,3,7,101,18]，输出: 4。

解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

代码如下：

dp[i]表示以a[i]这个元素结尾的最长递增子序列的长度。

想求 dp[5] 的值，也就是想求以 nums[5] 为结尾，其最长递增子序列。

nums[5] = 3，既然是递增子序列。我们只要找到，前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成新的递增子序列，而且这个新的子序列长度加一。

当然，可能形成很多种新的子序列，但是我们只要最长的，把最长子序列的长度作为 dp[5] 的值即可。

根据此依次类推到前面，d[0],d[1]…d[i]都是这样求出来的，看来动态规划有些是逆推的。
 

最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

输入: [-2,1,-3,4,-1,2,1,-5,4]，输出: 6，解释: 连续子数组 [4,-1,2,1] 的和最大，为 6

解决思路：动态规划

动态规划方程：

动态规划：定义dp[i]表示为nums[i]为结尾的[连续子数组的最大和。

当遍历到nums[i]时，我们需要比较nums[i]和dp[i-1]+nums[i]谁更大，然后取较大值。

代码如下：

责任编辑：lq