

一文秒懂贝叶斯优化/Bayesian Optimization
描述
今天想谈的问题是:什么是贝叶斯优化/Bayesian Optimization,基本用法是什么?
本文的定位是:帮助未接触、仅听说过、初次接触贝叶斯优化的小白们一文看懂什么是贝叶斯优化和基本用法,大神/贝叶斯优化专家们求轻喷,觉得不错的记得帮点赞/在看/转发帮扩散哦!谢谢。
梳理这个问题有这么两个原因:
1、在工业界,最近我看到不少同学在探索并使用贝叶斯优化的方法寻找更好的超参,找到performance更好的模型,涨点涨分;
2、家里另一位在学习和研究“Safety”强化学习的时候,发现一个“牛牛“的代码是基于贝叶斯优化的,为了提高家庭地位不得不看一看啦哈哈哈。
于是之前仅仅只听说过贝叶斯优化的我,赶紧知乎治学,面向Github编程,面向谷歌解决问题,一通搜索学习了解入门之后基本有个框架和概念了,遂记录在此,望茫茫互联网看到这个文章的小白们也可以快速入门贝叶斯优化/Bayesian Optimization!
贝叶斯优化应用场景
如果你要 解决的问题/面对的场景,假设输入为x,输出为f(x),有如下特点,那不妨试一下贝叶斯优化吧。
这个函数f(x)特点是计算量特别大,每次计算都特别耗时、耗资源;
甚至f(x)可能都没有解析式表达式。
无法知道函数f(x)对于x的梯度应该如何计算。
需要找到函数f(x)在x自变量上的全局最优解(最低点对应的取值)
举例:
我们有一个参数量巨大的推荐系统模型(或者是某个NLP模型),每次训练很消耗资源和时间,但我们仍然期待找到更好的模型超参数让这个推荐系统的效果更好,而人工参数搜索太费神、Grid Search太消耗资源和时间,想找一个不那么费神同时资源消耗和时间消耗也比Grid Search稍微小一点的办法。
这个场景基本满足以上特点:一是计算量大、二是模型对于超参数(比如learning rate学习率,batch size)的梯度无从知晓;所以可以考虑用贝叶斯优化来寻找最合适的一组超参。对此实际应用感兴趣的同学可以进一步阅读:Facebook efficient-tuning-of-online-systems-using-bayesian-optimization。
但这儿还是要给想用贝叶斯优化寻找超参的同学稍微泼以下冷水:由于实际系统的复杂性、计算量超级巨大(或者说资源的限制),可能连贝叶斯优化所需要的超参组合都无法满足,导致最后超参搜索的结果不如一开始拍脑袋(根据经验的调参)效果好哦。所以这是一个办法,但最好不是唯一办法哦。
一个关于Safe RL的例子:强化学习中的一个环境里有Agent A(比如一个小学生学如何骑自行车)在学习如何根据环境做出action,同时又有一个Agent B在帮助Agent A进行学习(比如有个老师担心宝贝学生摔倒,要教学生骑车)。Agent B需要从多种策略(每个策略还有一些参数)里找到一个最优的策略组合帮助Agent A进行学习(比如学自行车的时候自行车旁边放个2轮子、带个头盔,或者直接用手扶着,或者直接推着推着突然放手)。那么Agent B的如何选择最优辅助策略组合以及对应策略的参数也可以使用贝叶斯优化。感兴趣的同学可以阅读NeurIPS 2020的Spotlight presentation文章:Safe Reinforcement Learning via Curriculum Induction。

图1 Safe RL中例子
有了使用场景,我们就会问什么是贝叶斯优化啦。
什么是贝叶斯优化
贝叶斯优化定义的一种形象描述。
分享Medium上这个不错的例子。
比如我们有一个目标函数c(x),代表输入为x下的代价为c(x)。优化器是无法知道这个c(x)的真实曲线如何的,只能通过部分(有限)的样本x和对应的c(x)值。假设这个c(x)如图2所示。
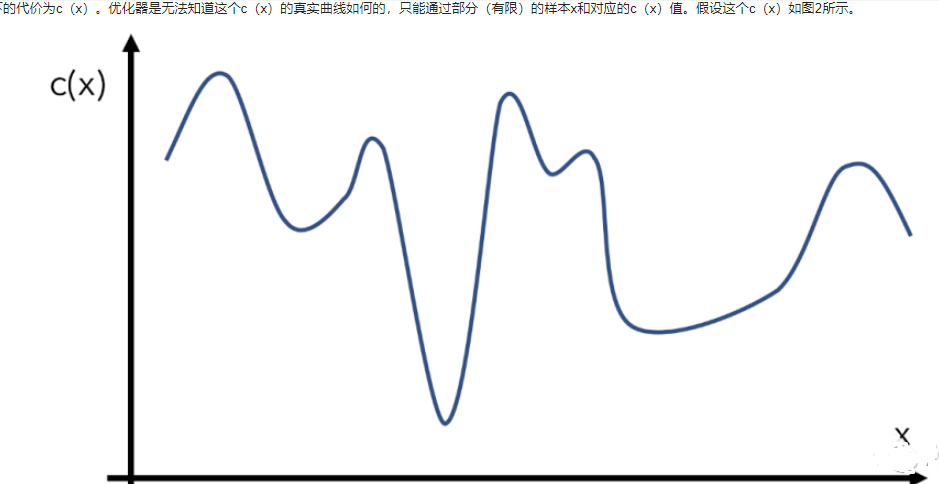
图2 优化函数举例
贝叶斯优化器为了得到c(x)的全局最优解,首先要采样一些点x来观察c(x)长什么样子,这个过程又可以叫surrogate optimization(替代优化),由于无法窥见c(x)的全貌,只能通过采样点来找到一个模拟c(x)的替代曲线,如图3所示:
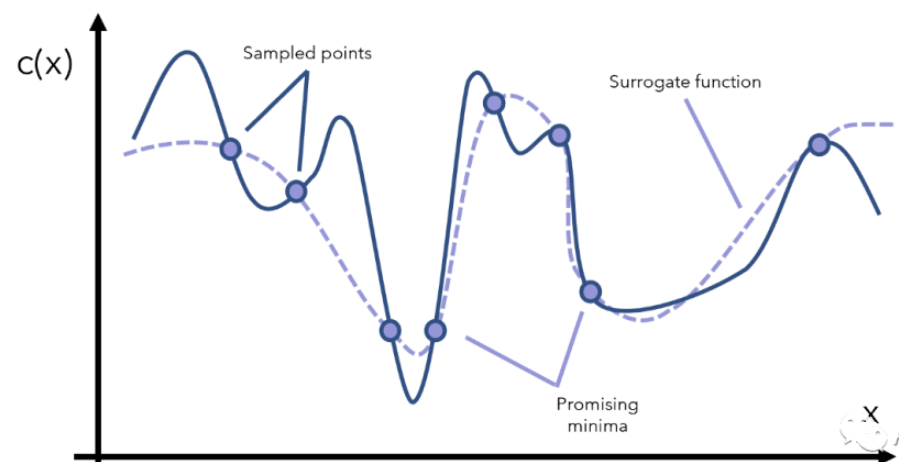
图3 采样的点与替代的曲线
得到这个模拟的/替代的曲线之后,我们就能找到两个还算不错的最小值对应的点了(图3中标注的是promising minima),于是根据当前观察到的这两个最小点,再采样更多的点,用更多的点模拟出一个更逼真的c(x)再找最小点的位置,如图4所示。
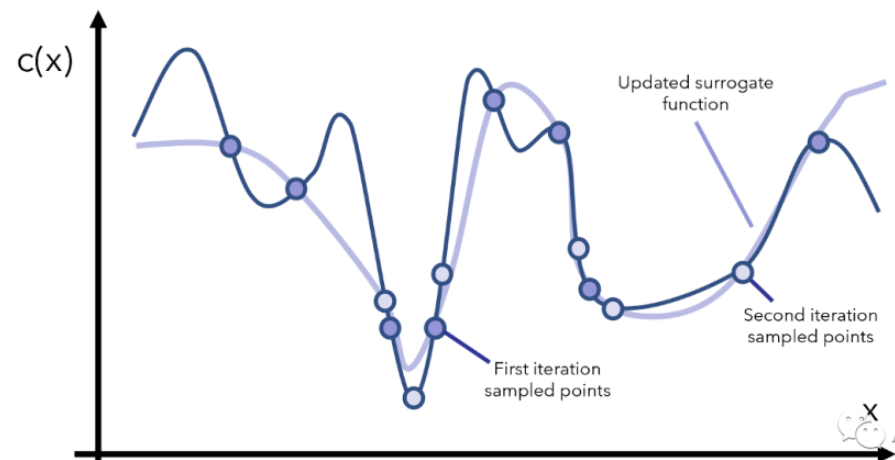
图4 继续采样 空心的圈为第2次采样的点
然后我们重复上面这个过程,每次重复的时候我们干以下几件事情:先找到可拟合当前点的一个替代函数,然后根据替代函数的最小值所在的位置去采样更多的 ,再更新替代函数,如此往复。
函数替代的例子: 给定x的取之范围,那么一个复杂的函数y = arcsin(( 1- cos(x) * cos(x)) / sinx) 则可以用y=x来替代。
如果我们的c(x)不是特别奇怪的话,一般来说经过几次迭代之后,我们就能找到c(x)的最优解啦。当然如果c(x)特别奇怪,那可能是数据的问题而不是。。。c(x)的问题。再回头来看上面这个过程,贝叶斯优化的厉害的地方:a 几乎没有对函数c(x)做任何的假设限定,也不需要知道c(x)的梯度,也不需要知道c(x)到底是个什么解析表达式,就直接得出了c(x)的全局最优。
以上例子中有两个重要的点:
1、用什么函数作为替代函数(选择函数进行curve-fiting的过程),对应Gaussian Processes;
2、如何根据当前信息和替代函数的局部最优点继续采样x,对应acquisition function。
为什么可以用Gaussian Processes对曲线进行拟合呢?
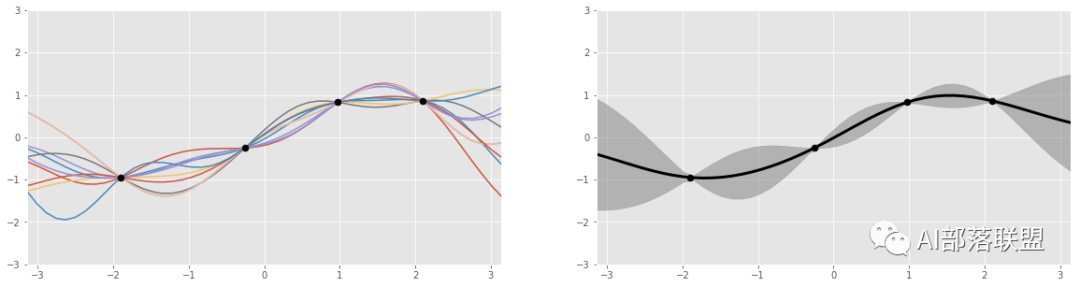
图5 总共4个黑色的点,代表4个数据点。左边是Gaussian process产生的多个函数曲线(红、蓝、黄等曲线);右边的图显示的是左图的那些函数都会经过黑点,以及函数值的波动范围(灰色部分)。
Gaussian Processes的一个非常大的优点:“先验知识”可以根据新观测量更新,而Gaussian Processes又可以根据这个更新后的“先验知识”得到新的function的分布,从而更好的拟合数据点。也就是:如果我们观测了3个函数值,那么有一种高斯分布和这三个观测的数据点对应,而如果我们观测了4个点,又可以新计算一个对应的高斯分布。
这里我们简单以图6为例描述一下:Gaussian Process是如何根据拟合数据,然后对新的数据做预测?
如图6所示,假设现已观测到3个点(左边黑色的3个圈),假设这计算得到3个函数值分布是 ,Gaussian Process的理论告诉我们(具体理论先略了)给定一个新的 输入 (左图蓝色 ),我们可以按照图6左下角的方式计算出与蓝色 对应的 的均值和方差,也就是输出的范围。
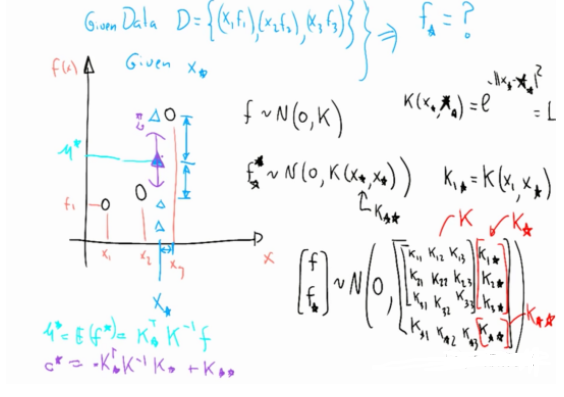
图6 更新过程示意图
acquisition function在决定如何选取新的采样点是面临两个经典问题:exploitation和exploration,我称之为深度和广度。以图5的例子来看,
exploitation意味着尽可能顺着当前已知的信息,比如顺着黑色点的地方来采样更多的点,也就是深度。当已知信息利用到一定程度,这种exploitation方向的采样会很少有信息增益。
exploration顾名思义就是更趋向探索性质,比如顺着图5右边的灰色区域较大的地方探索,也就是广度,探索更多未知的地方。
假设我们把acquisition functin简写为aq(x),整个贝叶斯优化可以概括为:
基于Gaussian Process,初始化替代函数的先验分布;
根据当前替代函数的先验分布和aq(x),采样若干个数据点。
根据采样的x得到目标函数c(x)的新值。
根据新的数据,更新替代函数的先验分布。
并开始重复迭代2-4步。
迭代之后,根据当前的Gaussian Process找到全局最优解。
也就是说贝叶适优化实际上是:由于目标函数无法/不太好 优化,那我们找一个替代函数来优化,为了找到当前目标函数的合适替代函数,赋予了替代函数概率分布,然后根据当前已有的先验知识,使用acquisition function来评估如何选择新的采样点(trade-off between exploration and exploitation),获得新的采样点之后更新先验知识,然后继续迭代找到最合适的替代函数,最终求得全局最优解。
贝叶斯优化偏公式的定义,个人还是更喜欢公式定义的。
Bayesian Optimization(BO)是对black-box函数全局最优求解的一种strategy。具体的 是一个定义在 上L-Lipschitz连续的函数,我们想要找到 的全局最优解:
这里我们假设函数 是一个black-box,对于这个black-box,我们只能观测到有噪声的函数值: 其中 ,也就是零均值高斯分布。于是整个优化目标可以变成:找到一系列的 使得 最小:
要让 被快速优化到最小,由于 对应了函数 这个最小点,所以越靠近 开始采样,那么采样得到的一系列 越快结束 的优化,也就结束了 全局最优解的优化。
这一序列 具体是如何得到的呢?假设我们在第 次iteration里采样到了 ,我们将新观测到的数据加入到已有的观测数据 里,然后通过优化一个叫actuisition function 的函数得到下一个时刻要采样的 ,也就是 。
那么这个 要如何设计呢?归根结底是如何根据已有的观测量选择 ,于是设计过程中就遇到了经典的exploration和exploitation问题,也就是是继续沿着已有的信息深挖,还是扩大信息的覆盖广度?
我们已有的观测量是 ,假设这些观测量服从高斯分布 ,其中 分别是均值和方差,也对应着exploitation和exploration(方差通常也指不确定性)。那我们就根据expatiation和exploration来设计 吧,这里只介绍一钟叫Gaussian Process-Upper Confidence Bound (GP-UCB)的设计:
很容易看出, a 其实就是均值和方差加权和,也就起到了调和exploitation和exploration的作用啦。至于其他几种acquisition function,Expected Improvement (EI),(Predictive) Entropy Search,Thompson Sampling(TS)等本文就不再一一描述啦。
有了 就能确定新的采样点了,Gaussian Process也就能跟着更新了,最终替代函数的拟合也就越来越贴近真实函数了,最终找到全局最优点。
结合上面的形象描述和公式定义描述,总结以下贝叶斯优化的两个重点:
1. 定义一种关于要优化的函数/替代函数的概率分布,这种分布可以根据新获得的数据进行不断更新。我们常用的是Gaussian Process。
2. 定义一种acquisition function。这个函数帮助我们根据当前信息决定如何进行新的采样才能获得最大的信息增益,并最终找到全局最优。
贝叶斯优化的应用
纸上得来终觉浅,绝知此事要躬行。
我们就用python来跑几个例子看看吧。以下例子需要安装Gpy和GpyOpt这两个python库。
假设我们的目标函数是:
这个函数定义在[-1,1]之间,通常也叫domain。这个函数的在定义区间的最优点是:x 。于是代码为:
import GPyOptdef myf(x): return x ** 2bounds = [{‘name’: ‘var_1’, ‘type’: ‘continuous’, ‘domain’: (-1,1)}]# 变量名字,连续变量,定义区间是-1到1max_iter = 15# 最大迭代次数myProblem = GPyOpt.methods.BayesianOptimization(myf,bounds)#用贝叶适优化来求解这个函数,函数的约束条件是boundsmyProblem.run_optimization(max_iter)#开始求解print(myProblem.x_opt)#打印最优解对应的x为-0.00103print(myProblem.fx_opt)#打印最优解对应d的函数值为0.0004
总结
本文主要有以下内容:
写贝叶适优化的出发点。
贝叶适优化的适用场景。
贝叶适优化是什么?(包括一个形象和一个公式化的解释)。
贝叶适优化的应用例子。
那么问一问自己,看懂了吗?
参考文献:
https://zhuanlan.zhihu.com/p/76269142
https://radiant-brushlands-42789.herokuapp.com/towardsdatascience.com/the-beauty-of-bayesian-optimization-explained-in-simple-terms-81f3ee13b10f
https://www.youtube.com/watch?v=4vGiHC35j9s
编辑:jq
全部0条评论

快来发表一下你的评论吧 !

