

详解S型加减速曲线规划算法总结
描述
做过运动控制的小伙伴都知道,S曲线很重要,下面一张动图对比一下,你就知道S曲线的好处:
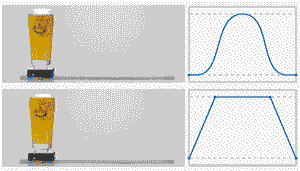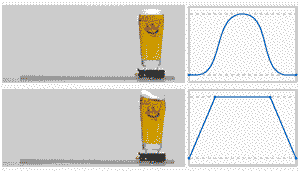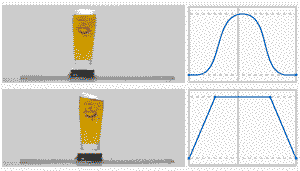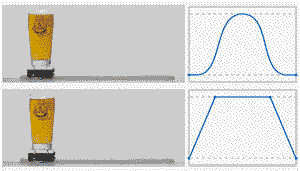
下面分享一下S曲线的内容:
1 前言
S形加减速的最重要特征是该算法的加速度/减速度曲线的形状如字母 S。S形加减速的速度曲线平滑 ,从而能够减少对控制过程中的冲击,并使插补过程具有柔性 [^1]。由于T形曲线在加速到匀速的切换过程中,实际中存在较大过冲,因此这里对比一下T曲线和7段S曲线的实际过程;
T形:加速 -》 匀速 -》 减速
S形:加加速() -》 匀加速() -》 减加速()-》 匀速()-》 加减速()-》 匀减速()-》 减减速()
上文在加速这块的文字描述可能读起来起来有点绕,下面看图:
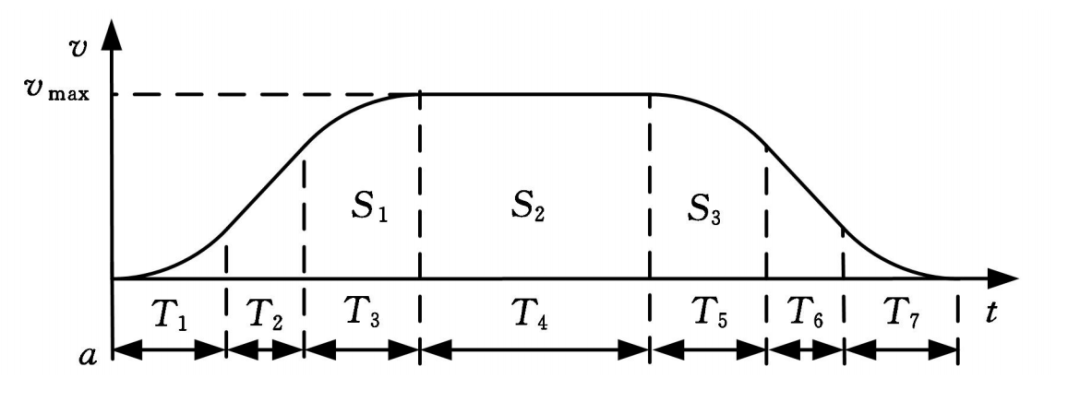
2 理论
分析由于S曲线在加减速的过程中,其加速度是变化的,因此这里引入了新的一个变量 ,即加加速度。
因此对应上图的7段S速度曲线中,规定最大加速为,最小加速度为,则加速度的关系;
加加速():逐渐增大;
此时
匀加速():达到最大;
此时
减加速():逐渐减小;
此时
匀速():不变化;
此时
加减速(): 逐渐增大;
此时
匀减速(): 达到最大;
此时
减减速(): 逐渐减小;
此时
“为加速度的绝对值;其中
所以通常需要确定三个最基本的系统参数 :系统最大速度 ,最大加速度a_{max} ,加加速度,就可以可确定整个运行过程[^2] ;
最大速度:反映了系统的最大运行能力 ;
最大加速度:反映了系统的最大加减速能力 ;
加加速度:反映了系统的柔性;
柔性越大,过冲越大,运行时间越短;
柔性越小,过冲越小,运行时间越长;
2.1 加速度时间关系方程
整个加速度变化的过程具体如下图所示;
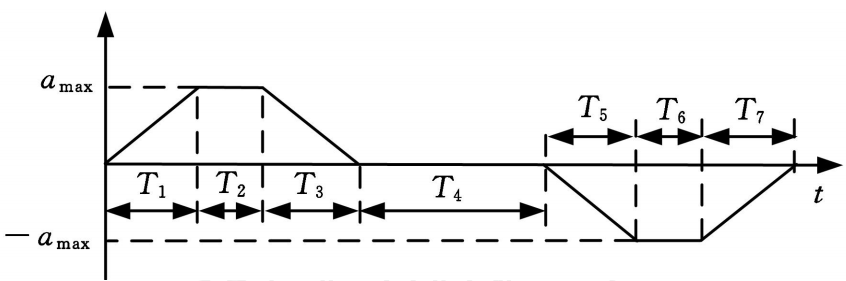
再次强调一下 和 的关系,另外这里再引入变量 ,
比如,当前时刻 ,即 位于区间 ,则如果将 作为初始点,则 为 相对于时刻的时间,则有:
下面可以得到加速度与时间的关系函数,具体如下:
根据 ① 式,将 代入 ② 式可以得到:
上式中 ;
2.2 速度时间关系方程
速度和加速度满足 ;加加速度和速度的关系满足:
结合加速度时间关系并结合② 式可以得到速度曲线关系,具体关系如下图所示;
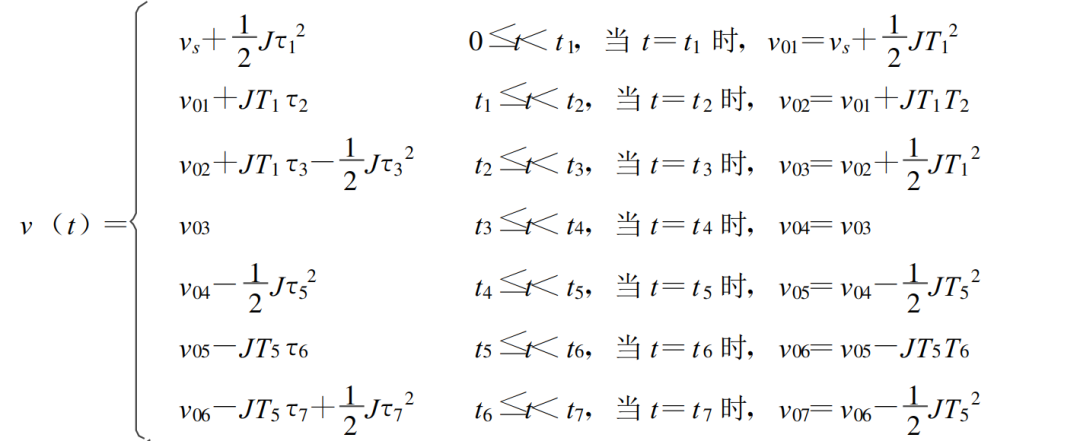
进一步简化可以得到:
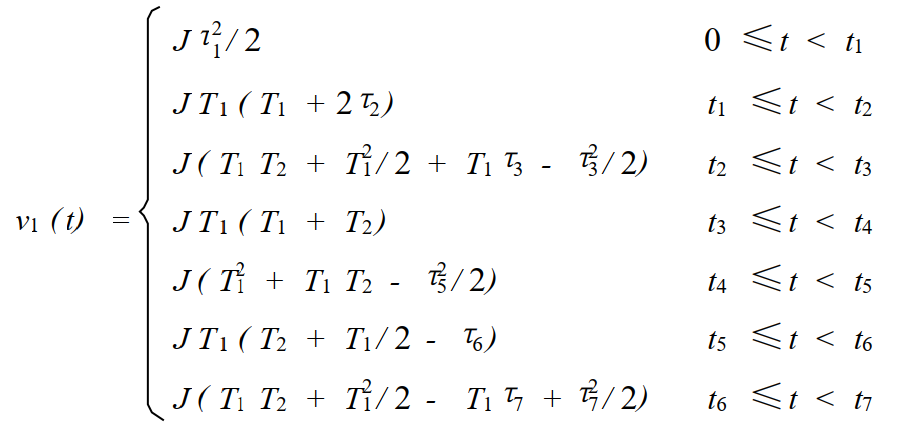
2.3 位移时间关系方程
位移 和加加速度 直接满足关系如下:
简单推导
因此可以得到:
“积分忘的差不多了,回去再复习一下;
最终位移的方程如下所示;
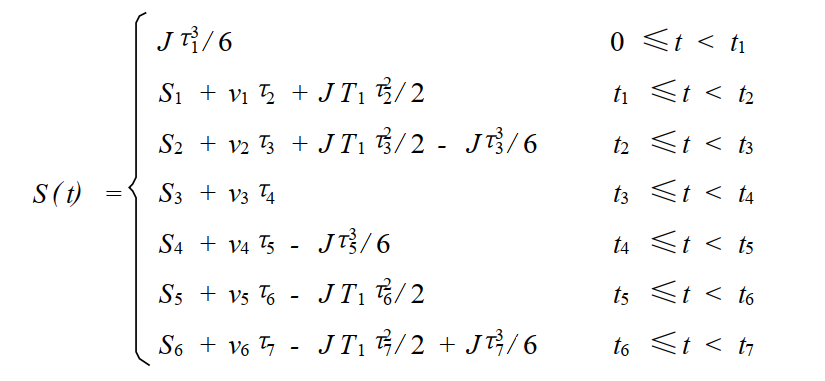
3 程序实现的思路
正如前面所提到的,S曲线规划需要确定三个最基本的系统参数 :系统最大速度 ,最大加速度a_{max} ,加加速度,这样就可以确定这个运行过程。这里有一个隐性的条件,就是在运行的过程中可以达到最大速度,这样才是完整的7段S曲线,另外这里还有一些中间参数:
,因此有 ;
加加速度 ;
;
,用户给定整个运行过程所需要的时间;
但是通常实际过程中关心,,;
3.1 推导
理想状态假设存在 和,则推导过程如下:
因此可以得到:
简化之后得到:
根据②式可知:
最终得到:
下面可以根据位移时间关系方程进行离散化的程序编写。
假设可以到达最大速度,且用户给定了整个过程运行时间,则 的推导如下:
简化上式可以得到:
根据 代入上式可得:
3.2 的推导
这时候还剩下需要计算,通过已量 可以推导出来;首先位移之间满足关系如下:
其中加速区长度为 ;其中减速区长度为 ;
具体推导;[^2]前面提到过,,因此在=0的时候,则
这里简单推导一下:
根据④,⑤最终简化得到:
“:为运行的总时间:为运行的总路程
详细推导过程如下:
因为:
因为:
所以,简化得到:
所以可以得到:
因为:
将其代入可以得到:
简化得到最终结果:
4 matlab
程序matlab程序亲测可以运行,做了简单的修改,因为这里直接给定了整个运行过程的时间,所以需要在SCurvePara函数中求出加加速度 的值,路程为 1:
SCurvePara
function [Tf1,V,A,J,T] = SCurvePara(Tf, v, a)
T = zeros(1,7);
for i=1:1000
% 加加速度 J
J = (a^2 * v) / (Tf*v*a - v^2 - a);
% Tk
T(1) = a / J;
T(2) = v / a - a / J; % t2 = v / a - t1;
T(3) = T(1);
T(4) = Tf - 2 * a / J - 2 * v / a; % t4 = Tf - 4*t1 - 2*t2;
T(5) = T(3);
T(6) = T(2);
T(7) = T(1);
% 根据T2和T4判断S曲线的类型
if T(2) 《 -1e-6
a = sqrt(v*J);
display(‘t2《0’);
elseif T(4) 《 -1e-6
v = Tf*a/2 - a*a/J;
display(‘t4《0’);
elseif J 《 -1e-6
Tf = (v^2 + a) / (v*a) + 1e-1;
display(‘J《0’);
else
break;
end
end
A = a;
V = v;
Tf1 = Tf;
end
SCurveScaling
function s = SCurveScaling(t,V,A,J,T,Tf)
% J = (A^2 * V) / (Tf*V*A - V^2 - A);
% T(1) = A / J;
% T(2) = V / A - A / J; % T(2) = V / A - T(1);
% T(3) = T(1);
% T(4) = Tf - 2 * A / J - 2 * V / A; % T(4) = Tf - 4*T(1) - 2*T(2);
% T(5) = T(3);
% T(6) = T(2);
% T(7) = T(1);
%%
if (t 》= 0 && t 《= T(1))
s = 1/6 * J * t^3;
elseif ( t 》 T(1) && t 《= T(1)+T(2) )
dt = t - T(1);
s = 1/2 * A * dt^2 + A^2/(2*J) * dt.。.
+ A^3/(6*J^2);
elseif ( t 》 T(1)+T(2) && t 《= T(1)+T(2)+T(3) )
dt = t - T(1) - T(2);
s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt 。..
+ 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t 》 T(1)+T(2)+T(3) && t 《= T(1)+T(2)+T(3)+T(4) )
dt = t - T(1) - T(2) - T(3);
s = V*dt 。..
+ (-1/6*J*T(3)^3) + 1/2*A*T(3)^2 + (A*T(2) + A^2/(2*J))*T(3) + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t 》 T(1)+T(2)+T(3)+T(4) && t 《= T(1)+T(2)+T(3)+T(4)+T(5) )
t_temp = Tf - t;
dt = t_temp - T(1) - T(2);
s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt 。..
+ 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
s = 1 - s;
elseif ( t 》 T(1)+T(2)+T(3)+T(4)+T(5) && t 《= T(1)+T(2)+T(3)+T(4)+T(5)+T(6) )
t_temp = Tf - t;
dt = t_temp - T(1);
s = 1/2 * A * dt^2 + A^2/(2*J) * dt + A^3/(6*J^2);
s = 1 - s;
elseif ( t 》 T(1)+T(2)+T(3)+T(4)+T(5)+T(6) && t 《= T(1)+T(2)+T(3)+T(4)+T(5)+T(6)+T(7) + 1e5 )
t_temp = Tf - t;
s = 1/6 * J * t_temp^3;
s = 1 - s;
end
end
测试的代码如下:TEST
%%
N = 500;
ThetaStart = 0; %起始位置
ThetaEnd = 90; %最终位置
VTheta = 90; %1 速度
ATheta = 135; %1.5 加速度
Tf = 1.8; % 总行程时间
v = VTheta/(ThetaEnd - ThetaStart);
a = ATheta/(ThetaEnd - ThetaStart);
v = abs(v);
a = abs(a);
Theta = zeros(1,N);
s = zeros(1,N);
sd = zeros(1,N);
sdd = zeros(1,N);
[TF,V,A,J,T] = SCurvePara(Tf, v, a);
display(J, ‘J:’);
display(TF,‘Tf:’);
display(V,‘v:’);
display(A, ‘da:’);
display(TF-Tf,‘dTf:’);
display(V-v,‘dv:’);
display(A-a, ‘da:’);
t=linspace(0,TF,N);
dt = t(2) - t(1);
for i = 1:N
if i == N
a = a;
end
s(i) = SCurveScaling(t(i),V,A,J,T,TF);
Theta(i) = ThetaStart + s(i) * (ThetaEnd - ThetaStart);
if i》1
sd(i-1) = (s(i) - s(i-1)) / dt;
end
if i》2
sdd(i-2) = (sd(i-1) - sd(i-2)) / dt;
end
end
subplot(3,1,1);
legend(‘Theta’);
xlabel(‘t’);
subplot(3,1,1);
plot(t,s)
legend(‘位移’);
xlabel(‘t’);
title(‘位置曲线’);
subplot(3,1,2);
plot(t,sd);
legend(‘速度’);
xlabel(‘t’);
title(‘速度曲线’);
subplot(3,1,3);
plot(t,sdd);
legend(‘加速度’);
xlabel(‘t’);
title(‘加速度曲线’);
看到最终仿真结果和预期相同;
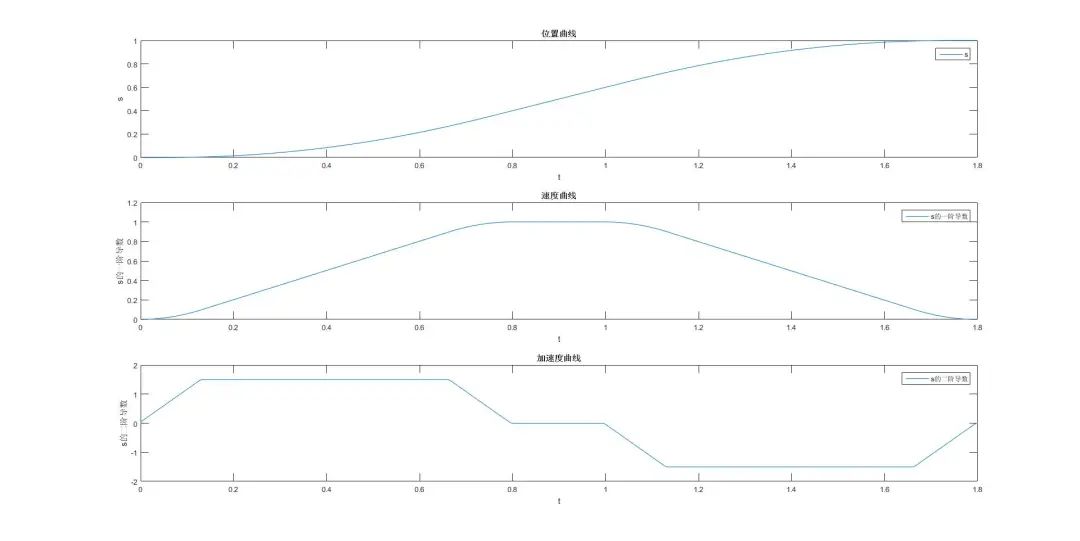
最后再看一下T形和S形速度曲线规划的效果对比:
5 总结
本文只对7段的S曲线规划做了详细的推导和介绍,matlab中的程序对于4段和5段都有做实现,很多是在理想情况下进行推导的,初始速度默认为0,终止速度也为0,并且假设加减速区域相互对称。最终运行结果符合预期效果。
“文中难免有错误和纰漏之处,请大佬们不吝赐教创作不易,如果本文帮到了您;
6 参考
[^1]:陈友东 魏洪兴 王琦魁。数控系统的直线和 S 形加减速离散算法[D]。北京:中国机械工程,2010.
[^2]:郭新贵 李从心 S 曲线加减速算法研究 上海交通大学国家模具 CAD 工程研究中心 , 200030
编辑:lyn
-
电机运动控制算法之S速度曲线规划算法2023-09-14 17461
-
步进电机S型曲线加减速算法与实现2023-03-21 741
-
怎么实现步进电机S型曲线加减速算法?2021-10-12 2495
-
电机的S型曲线规划的问题2021-09-03 1743
-
S型曲线加减速算法2021-08-31 3209
-
步进电机S型曲线加减速算法是什么?如何去实现?2021-07-08 940
-
步进电机的S型曲线加减速算法与实现2021-06-28 1802
-
如何实现S曲线加减速算法研究2021-03-26 2232
-
如何使用S曲线进行步进电机加减速的控制设计资料说明2019-03-13 2173
-
S曲线加减速控制新算法的研究2016-05-04 731
-
多轴联动线性插补及其_S加减规划算法2016-05-03 1128
全部0条评论

快来发表一下你的评论吧 !

