详解光学拓扑转变纳米光源调控技术

拓扑学（名词解释）是数学的一个分支，主要关注几何图形在连续形变后还能保持不变的一些性质。简单来讲，物体的拓扑数可以由其开孔数量决定，例如一个球形的实心橡皮泥和勺子的开孔数为零，可以视为同一类拓扑相，而甜甜圈的开孔数为一，则为另外一类拓扑相。

近几十年来，物理学家将拓扑学的概念引入凝聚态物理，三位先驱者David J. Thouless、F. Duncan M. Haldane 和J. Michael Kosterlitz 也因为他们在拓扑相变和拓扑物态方面的贡献获得2016年诺贝尔物理学奖。

除凝聚态物理之外，科学家还将拓扑学的概念引入到光学，逐步发展出了拓扑光子学领域。通过将光子晶体能带理论和拓扑学结合，人们实现了多种光学拓扑态，具有许多新奇特性（例如完全抑制背散射等），在光通讯、光学集成和光子计算机等领域有巨大的应用潜力。

迄今为止，光学拓扑态的实验研究大多是在光波长较长的频段（例如微波），这是因为实现拓扑态往往需要破坏体系对称性，涉及复杂的结构设计。当光波长变小时（例如红外或可见频段），需要在纳米及以下尺度进行精细的结构设计，目前还受限于微纳加工的技术手段。因此，在纳米光子学领域（致力于在纳米尺度上实现光子操控）拓扑学还是一个比较陌生的概念。

2018年，W.Ma 等人（代表论文：Nature 2018， 562， 557 | 原文阅读）发现在一种天然的范德瓦尔斯晶体（α相氧化钼：α-MoO3）中存在声子极化激元（名词解释）。与之前观测到的极化激元不同的是，α-MoO3声子极化激元只能沿着特定的晶体方向（名词解释）传播，这是因为氧化钼是一种面内各向异性材料，即沿［100］和［001］晶体方向的介电常数不相等且为异号。

通过实验发现，α-MoO3声子极化激元的面内等频线（iso-frequency curve）是双曲线，这与常见的各向同性材料中闭合的圆形等频线非常不同。

基于上述发现，近期西班牙奥维耶多大学量子纳米光学小组报道了两种类型的光学拓扑转变（图1）。通过旋转双层氧化钼晶体或调控其介电环境，实现了光学拓扑转变的直接观测。这项研究有助于在纳米尺度下实现红外光的人为调控和高度定向传播。

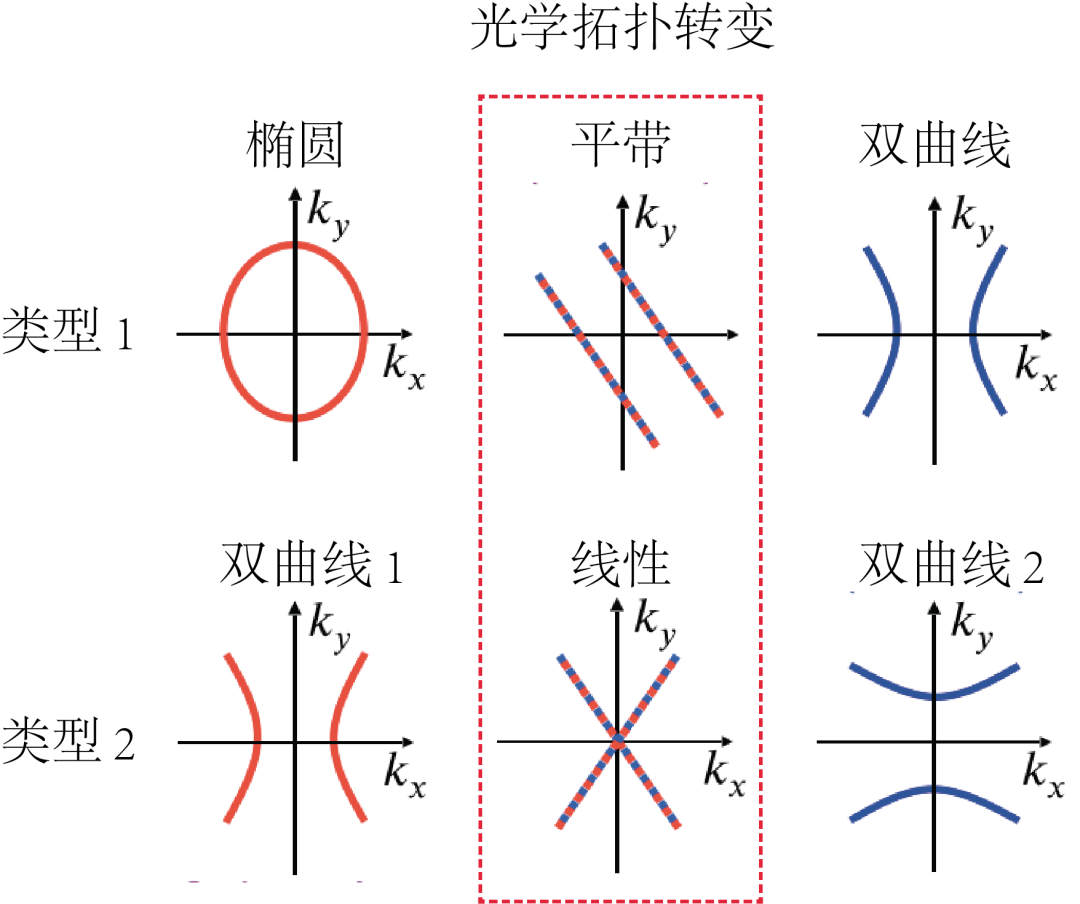
图1 两种类型的光学拓扑转变。

图中所示为极化激元的面内等频线。

在第一类拓扑转变中，

等频线由闭合的椭圆型变为开放的双曲线型。

第二类拓扑转变中，

双曲线型等频线闭合于一点然后重新打开并旋转了90度。

该成果分别以 Twisted Nano-Optics： Manipulating Light at the Nanoscale with Twisted Phonon Polaritonic Slabs 和 Enabling propagation of anisotropic polaritons along forbidden directions via a topological transition 为题发表在 Nano Letters 和 Science Advances。

第一类光学拓扑转变

理论研究表明当把两层氧化钼晶体叠加并且旋转一个固定角度时，由于层与层之间的电磁场耦合作用，声子极化激元的等频线会产生明显的变化，从而影响其传播（如图2所示）。

当转角为零度时，叠层氧化钼和单层氧化钼表现出类似的性质，极化激元的内陷型波前沿着［100］方向传播，即等频线为中心轴沿着［100］方向的双曲线；

当转角增大到63度时，极化激元变为沿固定角度高度定向传播，这说明其等频线变为了平带；

当转角继续增大到90度，极化激元可以沿所有面内方向传播，表明了闭合型等频线。

等频线从开口到闭合，说明其经历了拓扑转变。

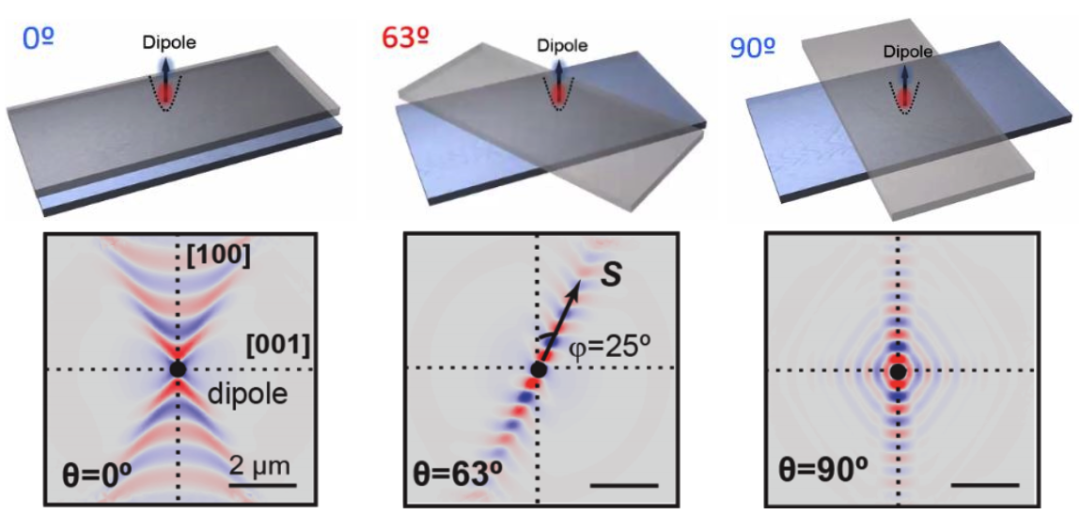
图2 光学拓扑转变的理论研究。

当双层氧化钼转角从零增大到90度时，

极化激元的传播方式发生了明显变化，

其等频线经历了从开口到闭合的拓扑转变。

为了在实验上直接观测此类光学拓扑转变，研究人员采用了扫描近场光学显微镜（s-SNOM）来表征氧化钼的近场光学分布。如图3所示，氧化钼表面的金纳米天线可以有效的聚焦红外光，从而激发极化激元，其光学信号通过针尖散射收集到探测器。

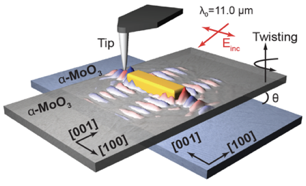
图3 扫描近场光学显微镜示意图。

金纳米天线可以有效的激发极化激元，

当用针尖在氧化钼表面逐点扫描后，

可以得到近场光学图像。

从图4中可以看到：

当双层氧化钼转角为30度时，极化激元表现为倾斜的内陷型波前，说明等频线为倾斜的开口双曲线；

当转角增大到54度时，极化激元只沿着一个方向传播，说明其等频线为平带；

当转角继续增大到90度时，极化激元可以沿着所有面内方向传播，说明其等频线为闭合型。

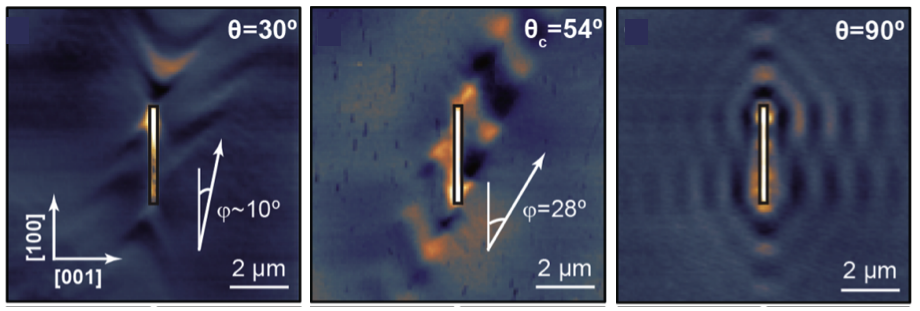
图4 不同转角双层氧化钼的近场光学图像。

极化激元的传播随着转角的不同发生很明显的变化，

表明了光学拓扑转变。

从实验中看到，通过改变双层氧化钼之间的转角，可以直观的看到从开口到闭合的光学拓扑转变，这与之前的理论研究一致。

需要强调的是这里的拓扑现象不同于拓扑光子学中陈数（名词拓展）的变化，而是类比于Lifshitz转变，即电子的能带可以从双曲线型（开口）变化到椭圆型（闭合），其性质会发生巨大的变化。

更加有趣的是，当等频线为平带时，极化激元只能沿一个方向传播，并且没有衍射，这是因为所有的Poynting矢量（名词解释）都沿着同一个方向。

如图5所示，通过比较发现，当转角为54度时，衡量衍射损耗的因子（f）为零，这与常见的极化激元有很大不同（f为0.5）。

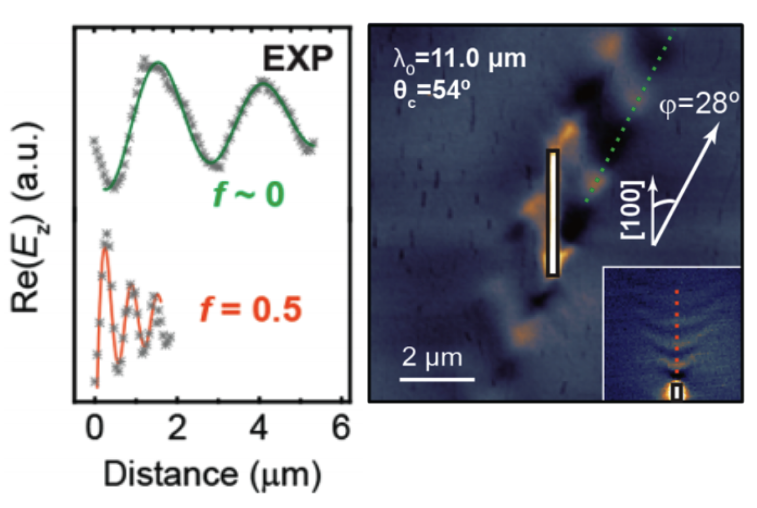
图5 极化激元的无衍射传播。

通过对比转角氧化钼和单层氧化钼发现，

当转角为54度时，

声子极化激元可以沿固定方向无衍射传播。

第二类光学拓扑转变

除了第一类光学拓扑转变外，我们还发现通过改变氧化钼周围的介电环境，可以实现第二类拓扑转变，即双曲线型的等频线经历闭合然后转向的过程。

理论研究（图6）表明，当氧化钼在二氧化硅衬底时，极化激元表现为中心轴沿着［100］方向的双曲线型等频线。然而，当我们把氧化钼放到碳化硅衬底时，极化激元表现为中心轴沿［001］方向的双曲线等频线，与二氧化硅衬底相比旋转了90度。

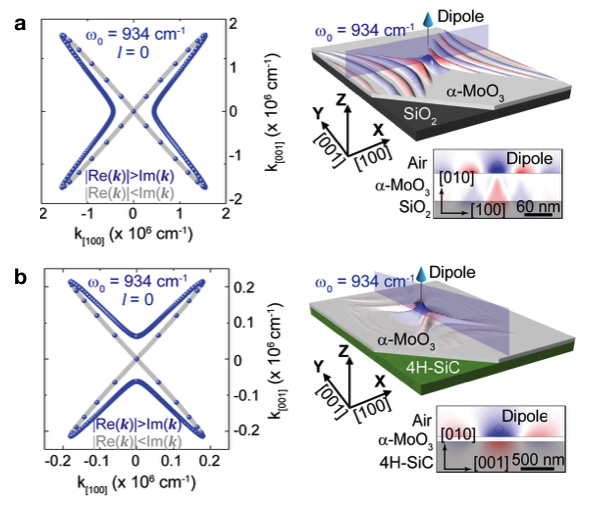
图6 不同衬底下氧化钼声子极化激元的比较。

当衬底为二氧化硅时，

等频线中心轴沿着［100］方向。

而当衬底为碳化硅时，

等频线中心轴变为［001］方向。

这是由于在红外波段，氧化硅的介电常数为正值，表现了一个常见的介质衬底，而碳化硅的介电常数为负值，存在表面声子极化激元，这就导致了氧化钼中极化激元和碳化硅极化激元的耦合，从而引起了体系内等频线的变化。

同样的，为了在实验中观测这一现象，我们采用s-SNOM获得了氧化钼在不同衬底下的近场光学图像。如图7所示，我们对比了二氧化硅和碳化硅衬底上氧化钼的近场光学图像，发现与理论预言一致：二氧化硅衬底上极化激元沿着［100］方向传播，碳化硅衬底上沿着［001］方向传播。这说明通过改变氧化钼的介电环境，不仅可以起到调控极化激元波长的作用，还可以控制其传播方向。

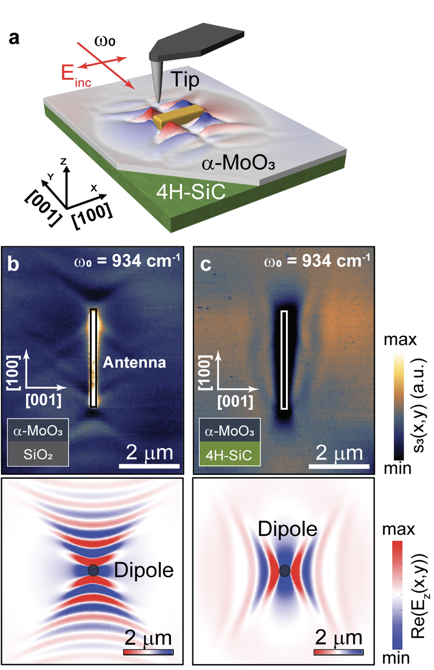
图7 不同衬底上氧化钼声子极化激元的近场光学图像。

a，扫描近场光学显微镜的示意图。

b，二氧化硅上氧化钼的近场光学图像和数值模拟。

c，碳化硅上氧化钼的近场光学图像和数值模拟。

为了进一步研究极化激元等频线旋转中涉及到的拓扑转变，我们改变入射光的频率对碳化硅上的氧化钼进行了近场光学表征（如图8所示）。

当入射光频率为948 cm-1时，极化激元沿着［100］方向传播，即等频线为中心轴沿着［100］方向的双曲线，这与氧化硅衬底的情况类似；

当入射光频率为937 cm-1时，极化激元变为沿着［001］方向传播，即等频线旋转了90度。

当入射光频率介于两者之间（943 cm-1），我们观测到了一种很奇特的等频线，为两条相交于一点的直线。

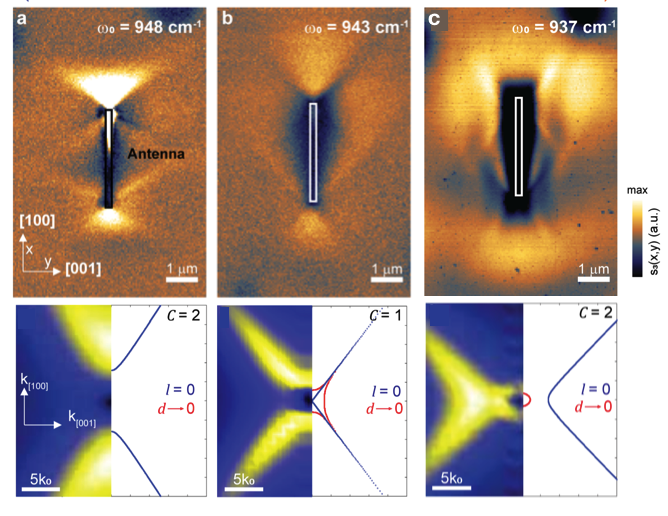
图8 不同入射光频率下极化激元的近场光学成像，

衬底为碳化硅。

当入射光频率逐渐减小时，

极化激元等频线经历了第二类光学拓扑转变。

这个实验表明：随着入射光频率的减小，等频线先为中心轴沿着［100］方向的双曲线，然后变为相交于一点的两条直线，最后变为中心轴沿着［001］的双曲线，与第二类光学拓扑转变一致（图1）。

为了进一步研究此类光学拓扑转变，我们从理论上计算了不同入射光频率下极化激元等频线的变化规律，如图9所示。当入射光频率为943cm-1时，双曲线变为了两条直线，并且相交于一点，直接证明了第二类拓扑转变。

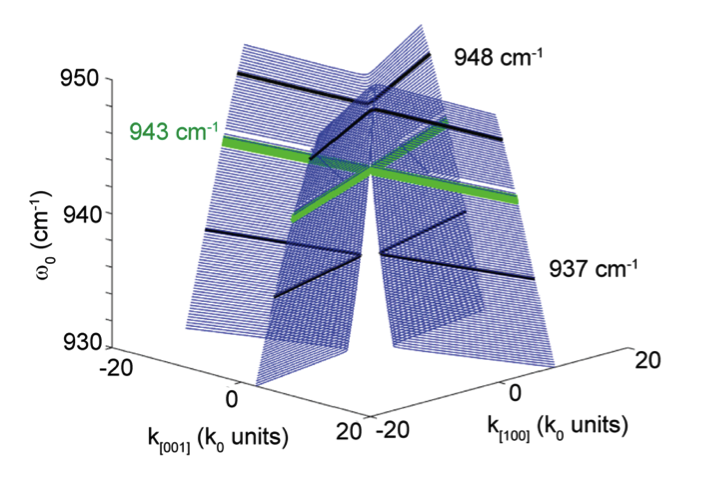
图9 碳化硅上氧化钼中极化激元等频线的理论计算结果。

当入射光频率为当入射光频率为943cm-1时，

双曲线变为了两条直线，并且相交于一点（绿色实线）。

将拓扑学的概念引入纳米光子学中有助于在纳米尺度下对光与物质相互作用以及光子传播的调控，也有助于从理论上理解光子的行为。

通过转角来调控天然范德瓦尔斯晶体的光学色散奠定了“转角光子学”的基础，对光子的调控提供了一个全新的维度。可以想象，光学拓扑转变带来的新奇物理现象会对光学成像，光子集成以及量子光学产生重要的影响。
编辑：lyn