简述HDL中循环语句的可综合性

在HDL的循环语句中，在指定的循环过程中，其代码块（循环体）输出同名信号，则构成顺序-循环（SAS-LOOP），其代码块（循环体）输出不同名信号，则构成并发-循环（CAS-LOOP）。

包括循环语句（含循环体）组成的代码块，EDA称为循环框架（Loop Frame）。

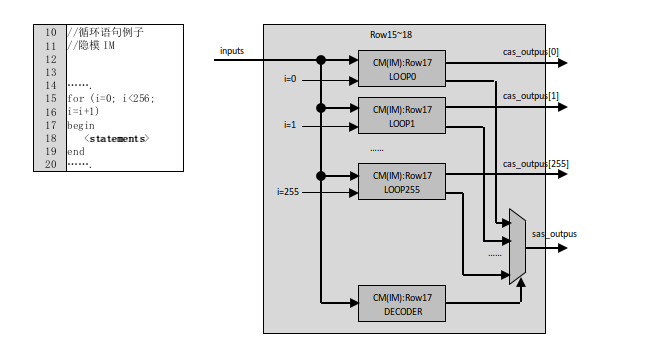
在这里，HDL循环语句与算法语言的循环语句的差异：

1.HDL的循环变量i是以常量进入循环体。算法语言则是以变量进入循环体。

2.HDL的循环体并不被循环执行，而是被重复描述（多次重复综合），从而实现建模的效率。算法语言的循环体则一定是被循环执行。

循环语句可综合性的“数学归纳法”

数学归纳法常用于证明数学序列，它的要点是：

1.首先证明序列的基数成立

2.假设序列为N时成立

3.证明序列的N+1成立

HDL的循环语句是否可综合，可以借用这个方法：

1.首先将循环语句的循环次数修改为一个很小的基数。由于在很小的基数时，其电路一定可以用结构化方法直接描述（不使用循环语句）

2.将基数加1，仍然可以是结构化描述，并加以验证

3.将基数修改为LPM参数可定制，使用循环语句描述，并加以验证

4.修改LPM定制参数，将其加1，观察其综合结果（验证）

通过以上步骤，可以证明所编写的HDL循环语句是可综合的，并且具有很高的综合效率。

循环语句设计例子：具有64个输入端口的8位异或电路：

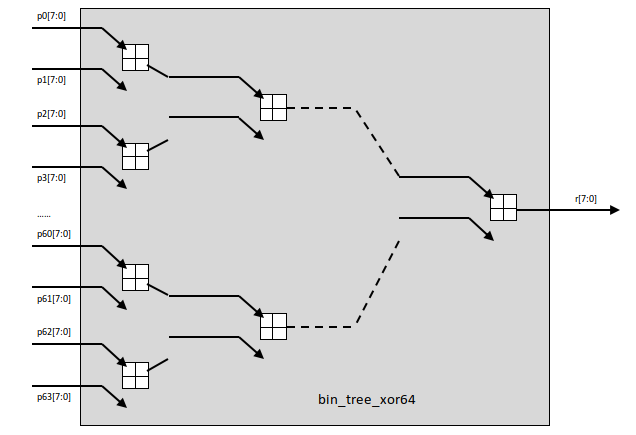
使用“数学归纳法”为其使用循环语句建模和验证：

1.将基数（端口数）设定为4，得到：

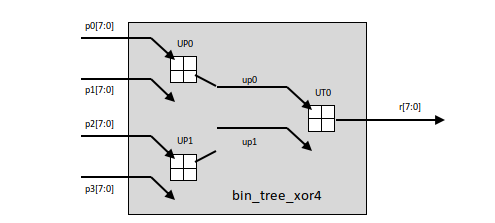
RTL视图（验证过程）：

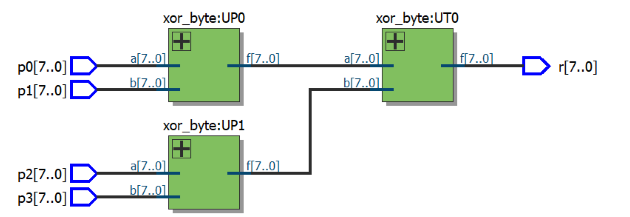
2.将基数加1，这里将端口数修改为8，得到：

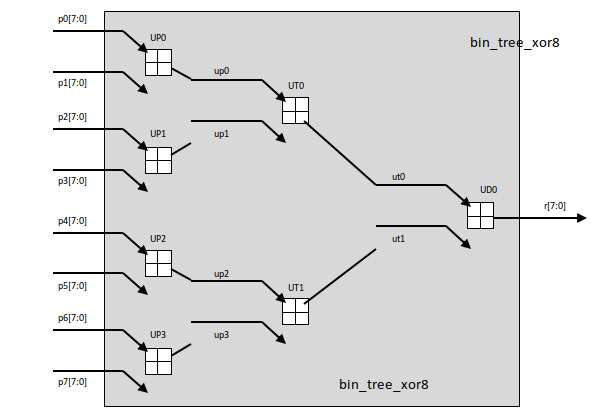
RTL视图（验证过程）：

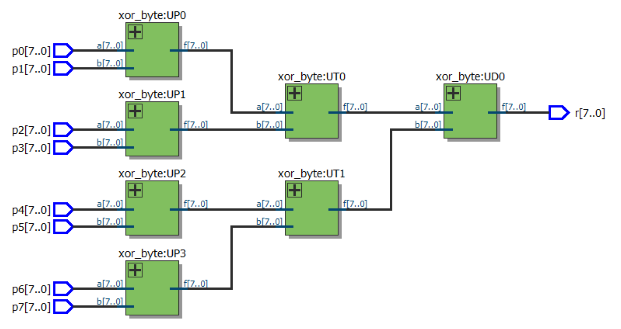
修改为端口数可定制的LPM模型

其RTL视图：

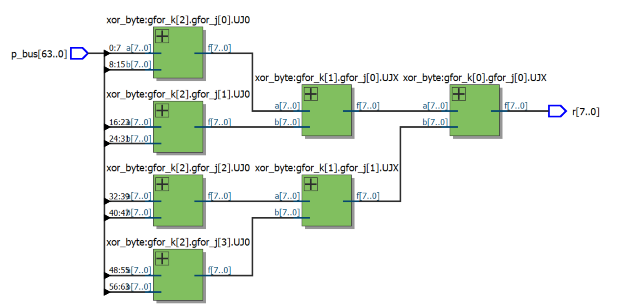
现在将LPM的基数+1（修改端口指数PortNum_Power为4）

其RTL视图：

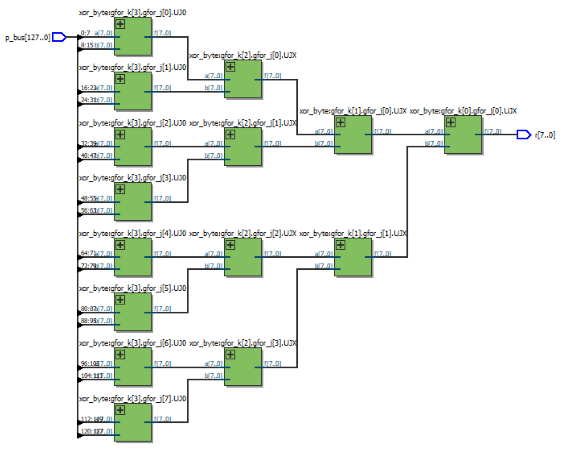
以上就是循环语句构成二叉树异或门的过程，为了得到最终结果（64端口），将端口指数PortNum_Power=6，得到：

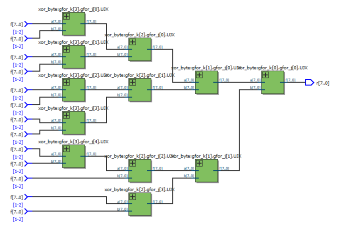
这里由于端口数过多，EDA的自动绘图需要中间过程，故首层仅展示如上部分。

循环语句可综合性的设计例子二：同步计数器的结构化设计

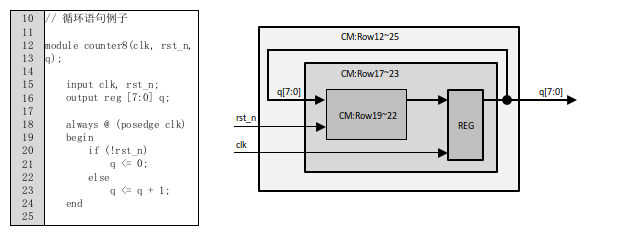
1.顶层框图

2.代码和代码模型分析

其RTL视图：

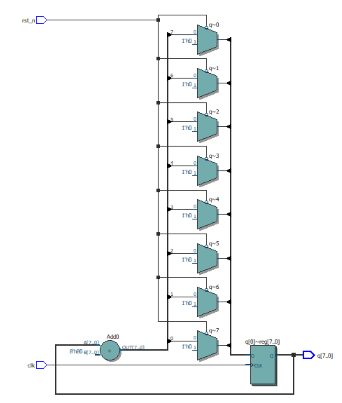
以上视图中，当rst_n=0时，多路器指向常数0；当rst_n=1时，多路器指向加法器的输出；注意加法器是寄存器的输出q与1相加。

根据代码模型和RTL视图，可以得到等效节点模型：

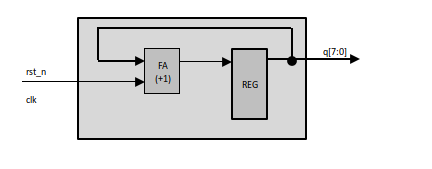
若将复位信号的条件语句描述屏蔽，则得到RTL视图更接近节点等效：

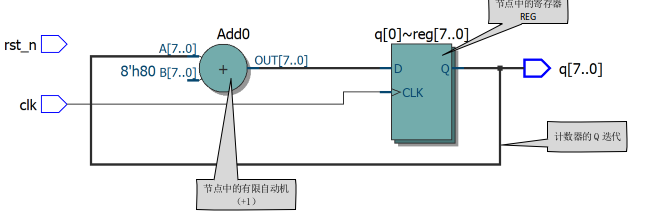
3.计数器的数学模型

在RTL视图中，计数器有限自动机的加法器执行q+1(的描述)，其真实的电路是得到优化和简化的一个数学模型：

若Q序列表示为：

在时钟离散时刻，Q的变化为：

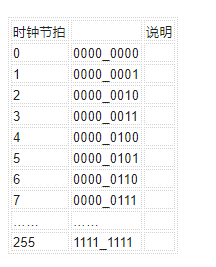
观察表格，能够发现Q的每一个比特位翻转的规律：

（）

（, ）

（, ）

……

（, ）

将触发翻转的条件（前级全部为1）采用级联以减少面积：

（，）

（, ）

（, ）

……

（, ）

式中：

…….

注意位翻转的一般表达式： （, ）

其真值表为：

其SOP为：

代入序列中，得到：

……

根据数学模型得到的代码模型为：

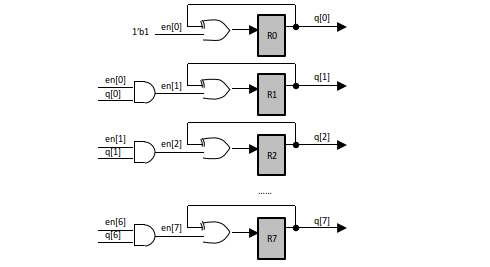
编辑：jq