

如何计算集成斩波放大器的ADC失调误差和输入阻抗?
电子说
描述
典型DPD应用
典型DPD应用模数转换器(ADC)中集成的缓冲器和放大器通常是斩波型。有关这种斩波实现的例子,可参见AD7124-8 和AD7779数据手册。需要这种斩波技术来最大程度地降低放大器的失调和闪烁噪声(1/f ),因为与其他工艺(如双极性工艺)相比,CMOS晶体管噪声高,难以匹配。通过斩波,放大器的1/f和失调转换到较高频率,如图1所示。
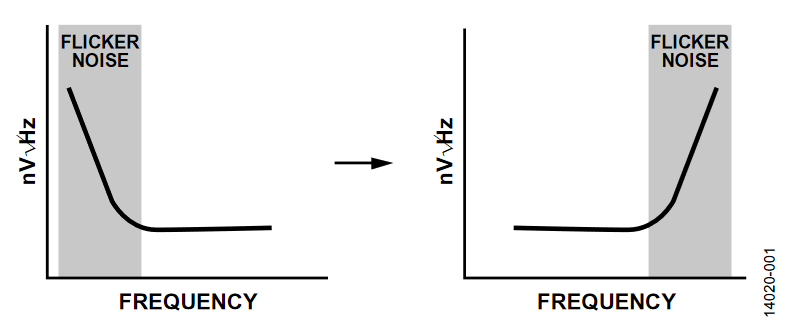
图1. 闪烁噪声(1/f )与斩波
在斩波转换过程中,开关的电荷注入会引起电流尖峰,进而使施加于ADC输入端的电压产生方向不定(流入和/或流出)的下降或尖峰。压降与连接到ADC输入段的传感器的输出阻抗成比例。
平均电流值
一般而言,数据手册不会提供电流峰值,因为它难以测量,而且不会增加任何有意义的信息。该信息之所以无意义,是因为缓冲器的斩波频率高于ADC的输入信号带宽。因此,输入引脚上添加的低通滤波器(用来消除高于奈奎斯特频率的频率或信号音,或用来降低耦合噪声)会对峰值电流进行平均,如图2所示。
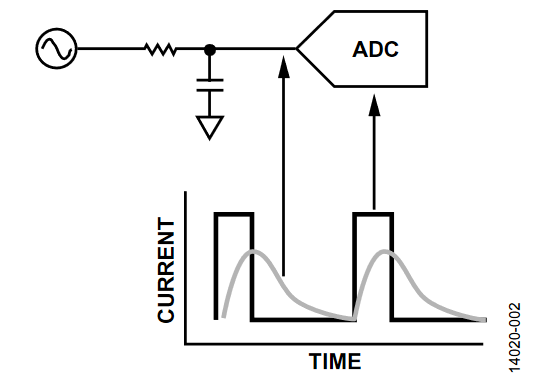
图2. 输入电流与时间的关系
用电流表测量输入电流,一端连接到VDD/2,另一端连接到ADC的模拟输入引脚。
如果电流表连接到其中一个电压轨,由于输入电压裕量的关系,测得的电流可能高于数据手册中的规格值。
输入电流与输入阻抗的关系
输入阻抗规格对精确计算直流误差没有帮助,因为与ADC内部输入阻抗引起的负载效应相比,输入偏置电流是最主要的贡献因素。
有两个规格与输入偏置电流相关:绝对电流和差分电流。绝对值(IABSOLUTE)是在任意模拟输入引脚测得的输入电流。差分输入电流(IDIFFERENTIAL)是在模拟输入引脚对之间测得的电流差。这仅适用于差分输入ADC。
如何计算直流误差
输入电流产生一个失调电压(VOFFSET),后者与连接到输入引脚的阻抗直接相关。
如图3所示,产生的失调电压一般为:
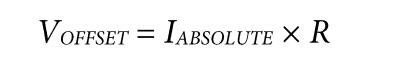
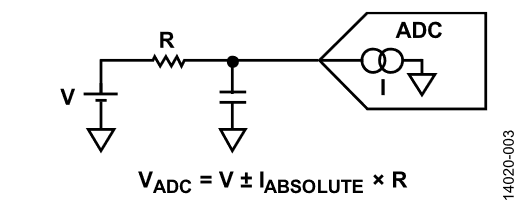
图3. 漏电流引起的压降
如果用运算放大器等低阻抗源驱动模拟输入引脚,误差将不很明显。
ADC测得的误差取决于施加的输入信号类型,例如是真差分输入信号还是伪差分/单端输入信号。
对于真差分输入信号,假设输入电阻(R)完全匹配,那么ADC测得的误差将是由模拟输入引脚对之间的差分输入电流引起,如下式所示:
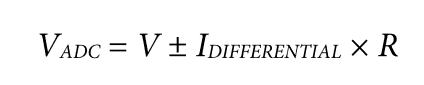
其中,VADC为ADC输入电压。
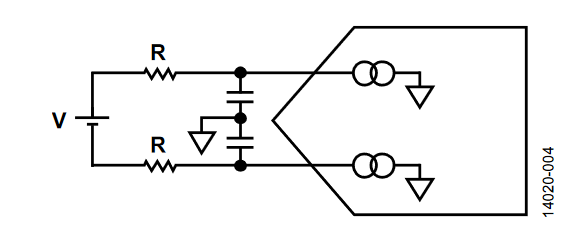
图4. 差分输入ADC
如果电阻不是完全匹配,则在差分输入电流贡献之外,电阻不匹配也会产生一个误差。
一般而言,假设电阻容差为1%,那么最差情况下的失调电压定义如下:
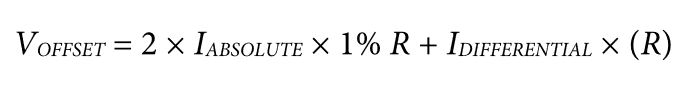
对于伪差分/单端输入信号,有两种情况:
一个模拟输入连接到低阻抗源(参见图5)。误差定义为:
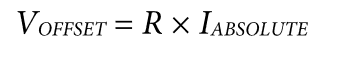
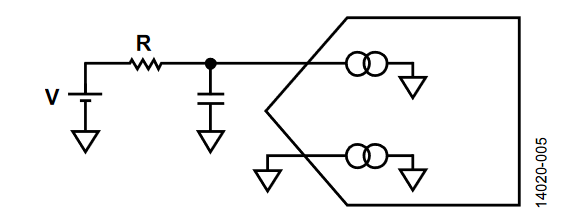
图5. 伪差分/单端ADC
两个输入均连接到高阻抗源(参见图6)。误差与使用真差分信号的情况相同。
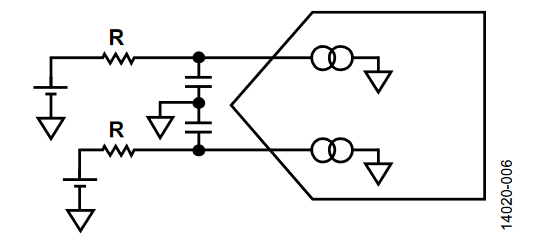
图6. 伪差分ADC
交流误差
交流分量与输入阻抗规格直接相关。输入阻抗可以是阻性或容性。若输入阻抗为容性,则给定频率下的阻抗计算如下:
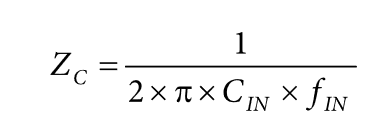
其中:
Zc为输入阻抗。
CIN为数据手册给出的输入电容。
fIN为输入频率。
举个例子,假设有8 pF电容和1 kHz输入带宽,则最小输入阻抗约为20 MΩ。
误差最小化
为使低通滤波器中电阻不匹配引起的误差最小,最好使用小电阻和大电容,因为电阻产生的失调和约翰逊噪声较低。
编辑:jq
-
如何计算集成放大器ADC失调误差和输入阻抗?2023-12-15 625
-
仪表放大器输入阻抗怎么计算?2023-09-05 3597
-
如何计算集成斩波放大器的ADC失调误差和输入阻抗?2023-04-11 2048
-
AN-1392: 如何计算集成斩波放大器的ADC转换器的失调误差和输入阻抗2021-03-20 805
-
放大器的输入阻抗的模型与应用2021-01-02 3033
-
放大器的输入阻抗定义及模型计算公式方程的增益摘要2019-06-27 18955
-
请问ADC中的可编程增益放大器 ,斩波容性放大器的工作原理是什么2018-10-31 4190
-
怎么计算集成斩波放大器的ADC转换器的失调误差和输入阻抗2018-10-16 1567
-
集成斩波放大器的ADC转换器失调误差和输入阻抗之间的关系及计算方法2017-09-12 1468
-
如何计算集成斩波放大器的ADC转换器的失调误差和输入阻抗2017-02-09 1539
-
一种斩波失调稳定仪表放大器的研究与设计2012-05-14 6678
-
高输入阻抗AC缓冲放大器2009-09-28 1371
-
高输入阻抗缓冲放大器2009-03-20 831
全部0条评论

快来发表一下你的评论吧 !

