全面剖析阻抗及输入阻抗和输出阻抗

阻抗及输入阻抗和输出阻抗解析    

阻抗是电阻和电抗的统称，电阻和电抗最大的差异在于电阻限流（欧姆定律）的同时会消耗电能。而电抗只限流，不消耗电能（不做功）。电阻在直流电和交流电下都有限流作用，而电抗只在交流电环境中有限流作用。

输入阻抗（input impedance)是指一个电路输入端的等效阻抗。在输入端上加上一个电压源U，测量输入端的电流I，则输入阻抗Rin就是U/I。你可以把输入端想象成一个电阻的两端，这个电阻的阻值，就是输入阻抗。

在同样的输入电压的情况下，如果输入阻抗很低，就需要流过较大电流，这就要考验前级的电流输出能力了;而如果输入阻抗很高，那么只需要很小的电流，这就为前级的电流输出能力减少了很大负担。所以电路设计中尽量提高输入阻抗。

输入阻抗跟一个普通的电抗元件没什么两样，它反映了对电流阻碍作用的大小。

对于电压驱动的电路，输入阻抗越大，则对电压源的负载就越轻，因而就越容易驱动，也不会对信号源有影响；而对于电流驱动型的电路，输入阻抗越小，则对电流源的负载就越轻。

因此，我们可以这样认为：如果是用电压源来驱动的，则输入阻抗越大越好；如果是用电流源来驱动的，则阻抗越小越好(注：只适合于低频电路，在高频电路中，还要考虑阻抗匹配问题。)另外如果要获取最大输出功率时，也要考虑阻抗匹配问题。

输出阻抗

输出阻抗（output impedance) 含独立电源网络输出端口的等效电压源(戴维南等效电路）或等效电流源(诺顿等效电路）的内阻抗。其值等于独立电源置零时，从输出端口视入的输入阻抗。

无论信号源或放大器还有电源，都有输出阻抗的问题。输出阻抗就是一个信号源的内阻。本来，对于一个理想的电压源(包括电源)，内阻应该为0，或理想电流源的阻抗应当为无穷大。输出阻抗在电路设计最特别需要注意。

现实中的电压源，则做不到这一点，常用一个理想电压源串联一个电阻r的方式来等效一个实际的电压源。这个跟理想电压源串联的电阻r就是信号源/放大器输出/电源的内阻了。

当这个电压源给负载供电时，就会有电流I从这个负载上流过，并在这个电阻上产生I×r的电压降。这将导致电源输出电压的下降，从而限制了最大输出功率。

同样的，一个理想的电流源，输出阻抗应该是无穷大，但实际的电路是不可能的。

输出阻抗，是指电路负载从电路输出端口反着看进电路时电路所等效的阻抗，其实主要是针对能量源或者输出电路来说的，是能量源在输出端测到的阻抗，俗称内阻。

阻抗思维分析开关电路

如下图，V1持续向R1在输送电流，图中电流回路如绿色箭头所示。如果想控制电流流向R1，我们有哪些办法？

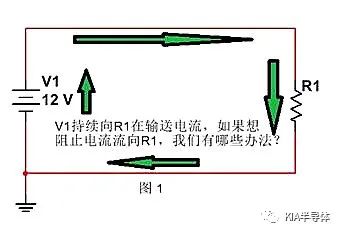
最常见的方法是，断开V1和R1之间的连接，切断电流回路。如下图所示。

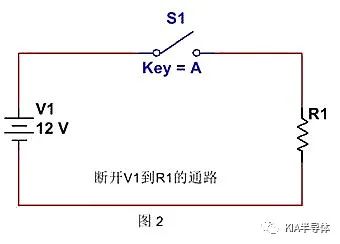
或者我们可以把R1旁路，如下图所示。将R1前面加一条导线，把电流引向阻抗低的通路上，R1上将获得忽略不计的电流。

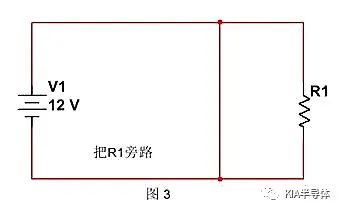
上述两种方法，都很直截了当，要么将V1到R1的通路彻底断开，要么短路R1，解决的很彻底。但是在工程的世界里，我们无法做的这么干脆利落，往往讲究个“差不多”就行。所以，“短路模型”我们只能做到“低阻抗”，“开路模型”我们只能做到“高阻抗”，能量被大幅度“衰减”，我们就认为达标了。

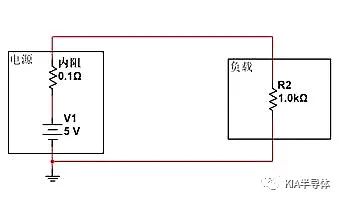
如下图所示，下图为实际的电源-负载模型。我们看如何通过调整阻抗来达到开关效果。实际电路中的电源都有输出能力限制和内阻，输出电流越大，输出电压也会越低。

如下内阻为0.1Ω，负载为1KΩ的电路。在当前情况下，负载两端获得的电压为内阻和R2分压而成。我们可以计算出V=5V*(1K/(1K+0.1))=4.9999V，I=5V/1000.1Ω=4.9mA。

如果我们用“开路模型”的方法来断开电路，该怎么调整阻抗呢？就是在电源和负载之间串接远大于1K的电阻，进行串联分压，使得R2上获得的电压更小。如下图，若串联的1M电阻与负载分压。我们可以计算出负载两端最终分配的电压：

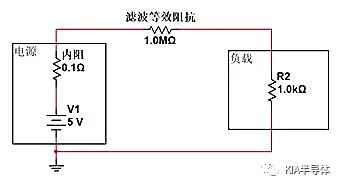
V=5V*（1K/（0.1+1000K+1K））=0.00499V，I=5V/1001000.1Ω=0.0049mA。幅值削弱了接近1000倍，在工程思维上，R2近似于被“断开”了。

如果我们用“短路模型”的方法来断开R2，该怎么调整呢？就是在负载前端并联远小于0.1Ω的电阻，与内阻进行串联分压，使得R2上获得的电压更小。

如下图，若滤波措施等效为并联的0.005Ω电阻与内阻分压。我们可以计算出负载R2两端最终分配的电压：

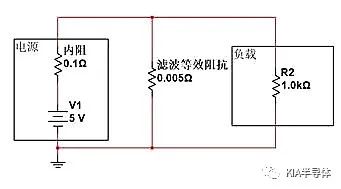
V=5V*（0.0049/（0.1+0.0049）=0.233V。幅值削弱了接近20倍，在工程思维上，R2同样近似于被“断开”了。

如上就是半导体开关电路的理论模型，以反相器电路为例：

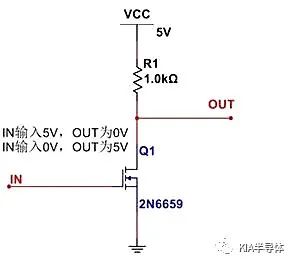
当IN端加高电平时，我们会说MOS管Q1导通。此时的导通状态相当于Q1变成了一个阻抗为几十毫欧的电阻，然后与R1电阻进行分压。假如上拉电阻R1太小，也为几十毫欧，那即使IN为高，Q1导通，OUT端也无法输出低电平。

当IN端加低电平时，我们会说MOS管Q1截止。此时的截止状态相当于Q1变成了一个阻抗为几兆欧的电阻，与R1电阻进行分压。假如上拉电阻R1太大，也为几兆欧，那即使IN为低，Q1截止，OUT端也无法输出高电平。

所以深入理解开关电路时，要以阻抗的思维去分析。

阻抗思维分析滤波电路

在此，用阻抗思维分析下滤波电路。

实际工程应用中，一个电源输出中往往包含不同频率的交流成分，有我们想要的，也有我们不想要的。而电感和电容的阻抗会随着频率变化。正是因为这个特点，电感和电容成了滤波电路中当仁不让的主角。

还是如下电路，假设该电源包含的频谱分量为0-1GHz。

假如我们要为负载R2滤除掉高频的交流分量，我们会发现串联电感或者并联电容的方式都可以满足要求。

如下图，若在电源和负载上串联1颗16uH的电感，100MHz交流分量会衰减多少？根据电感的阻抗公式：ZL=2πfL=2*3.14*100MHz*16uH，可以求得ZL=10K。

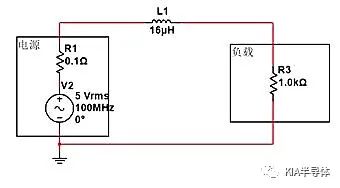
根据串联分压公式，R3两端电压/输入=R3/（R3+ZL）=1K/11K=0.0909。所以电源幅值为5V时，R3两端幅值仅为5V*0.0909=0.45V。

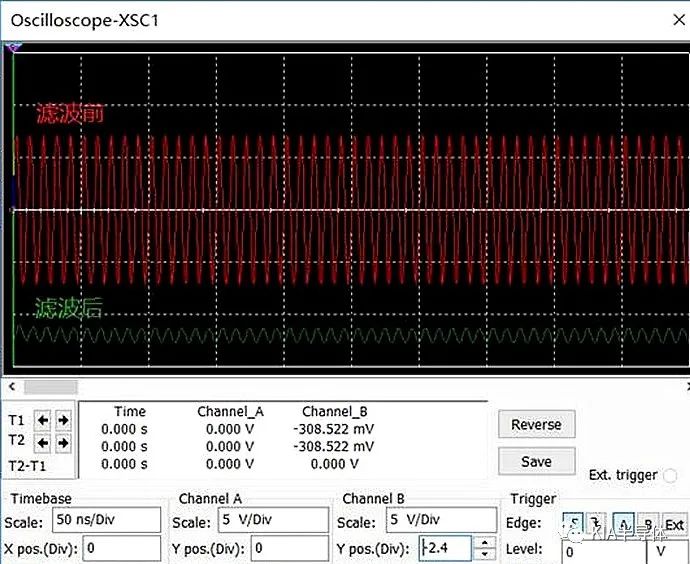
100MHz时，用示波器分别量测滤波前和滤波后的波形对比如下，可见100MHz波形效果，实际量测为0.449V，和分析结果一致。

阻抗思维分析低通滤波器

通过在电源和负载中间串联电感，在负载前端并联电容，就组成了低通滤波器电路。

如下，假如C1=1uF，L1=22uH，求该滤波电路对100MHZ交流分量的衰减程度是多少？

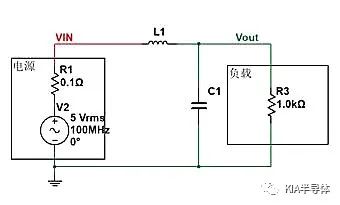
此时，该电路是电容(C1)的阻抗Zc和R3并联后，再和电感（L1）阻抗ZL进行分压。所以我们可以列出阻抗方程（就是简单的串联分压公式）。

衰减幅度=Vout/Vin=（Zc//R3）/(ZL+（Zc//R3）),

其中Zc=1/2πfC，ZL=2πfL。已知R3=1KΩ，可得

Zc=0.0015Ω，Zc//R=0.00149Ω。

ZL=13816Ω，可求得衰减幅度=0.00149/（13816.00149）=0.000000178。

可见100MHz的交流分量几乎无法通过22uH，1uF的低通滤波电路。同时我们也看到，负载R3也会影响滤波器滤波效果。所以我们有时候会发现同样的滤波器电路，在这个电路上效果好，别的电路上效果差。

编辑：jq