

如何正确理解系统的零输入响应
描述
系统的零输入响应是当系统没有外加激励信号作为输入时的响应。系统的输入信号去除以后,输出的响应信号一般不会突然消失。这是因为在输入信号去除之前,系统中的储能元件中一般总蓄有电磁,而这些能量不可能突然消失,它将逐渐释放出来,直至最后消耗殆尽。零输入响应正是由这种初始的能量分布状态,即初始条件所决定的。
为求系统的零输入响应,就要解下面式子所示的齐次方程。
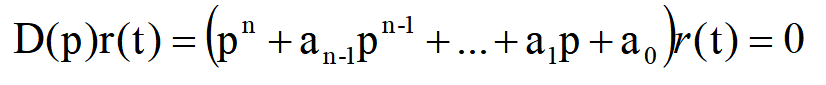
现在,先来讨论求解一阶和二阶齐次微分方程的简单情况。
一、一阶齐次微分方程

常数c可以根据初始条件t=0,r(t)=r(0)来确定c=r(0),于是得
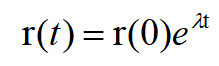
二、二阶齐次微分方程
再来看下二阶的齐次微分方程

可见,对于算子形式的微分方程,也可以像代数方程那样处理。
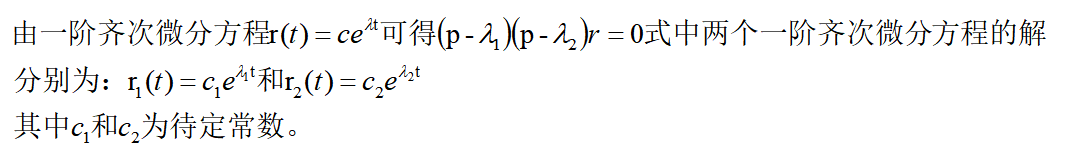
既然这两个解中任一个都能满足式
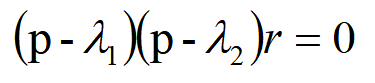
那么它们的和当然亦然能满足。所以二阶齐次方程解的一般形式应为:


三、n阶齐次微分方程
上述方法可以推广到求一般形式的齐次方程,为此先要把此式写成因式相乘的形式,即
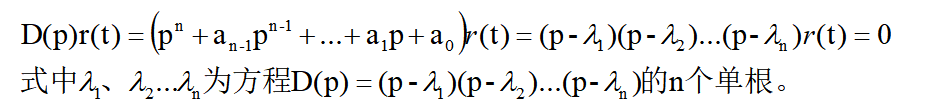
与二阶齐次方程的解相似,上面一般形式的齐次方程的解的一般形式应为:
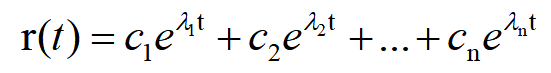
这也就是用n阶线性微分方程描写的系统的零输入响应的一般形式,它和拉普拉斯变换求解零输入响应导出的公式是完全相同的;
式中各λ就是复频域中转移函数的极点,它们决定了响应中的自然频率。
式中c1、c2、。。.、cn是n个初始条件确定的常数,显然为了确定这些常数,需要n个初始条件。
现在设初始条件t=0时,r(t)及其直到n-1阶的各阶导数的值r(0)、r‘(0)、r’‘(0)。。.,把这些初始值代入下式及其直到n-1阶的各阶导数式,得到下列联立方程组:
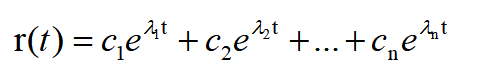
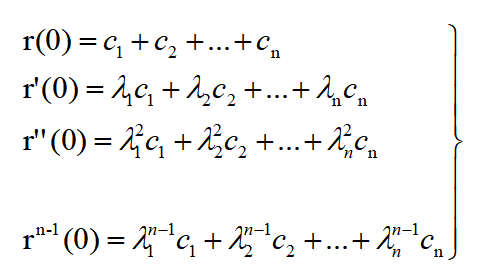
此联立式可以记为矩阵形式:
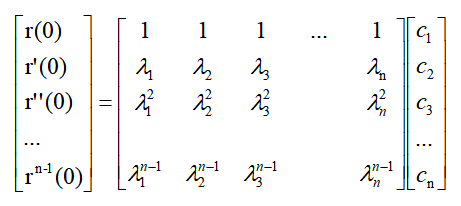

上面所示方程D(p)=0的根曾经假定全部是单根。如果有重根,那么方程的解也就不同于上面所示的简单形式。

这个解加上对应于方程D(p)=0的其他根的解,即为零输入响应函数的完全解。
编辑:jq
-
如何正确理解运算放大器输入失调电压?2023-12-07 1926
-
什么是二阶电路的零状态响应和零输入响应?零输入响应的步骤有哪些?2023-11-21 4930
-
应用笔记:正确理解驱动电流与驱动速度2022-01-27 5055
-
正确理解DC/DC转换器2021-11-16 2916
-
正确理解电路保护设计及器件选择资料下载2021-04-01 1091
-
什么是开关电源?正确理解开关电源的重要性2021-03-16 2692
-
如何正确理解磁滞损耗?2021-03-06 3240
-
如何正确理解GaN?2019-07-30 2776
-
正确理解时钟器件的抖动性能2013-06-21 19739
-
如何正确理解功率MOSFET的数据表(上篇).2012-08-13 3137
-
正确理解和测试信息技术设备的接地2010-01-08 1011
-
零输入响应和零状态响应2009-09-10 3379
-
零输入响应与零状态响应分析2009-05-10 19853
-
线性系统的零输入、零状态及完全响应2008-09-24 11120
全部0条评论

快来发表一下你的评论吧 !

