

你们知道什么是时域分析法 为什么需要卷积积分?
描述
分析线性系统的古典方法是微分方程法。描述系统的微分方程中,包含有激励函数和响应函数以及它们对时间的各阶导数的线性组合。线性系统的分析归结为求解线性微分方程。因为这样一个分析求解的过程,都是在时域中进行的,所涉及的都是时间变量t,所以这种解微分方程的方法称为时域分析法。
进行时域分析时,首先是列出系统的微分方程,这个工作并不困难。对于线性电路,只要根据基尔霍夫定理,就可以列出一个或一组电路的线性微分方程。
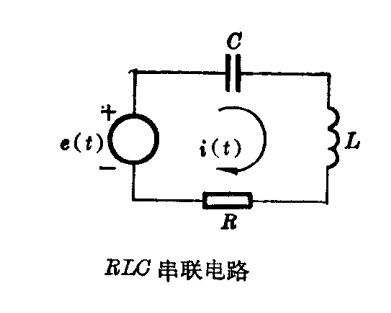
例如,对于RLC串联电路,如所熟知,可以列出如下方程:
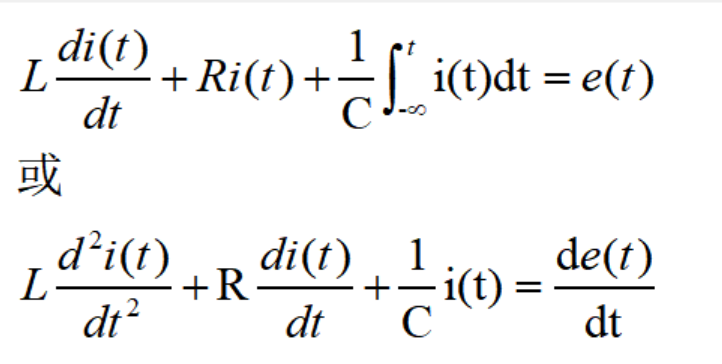
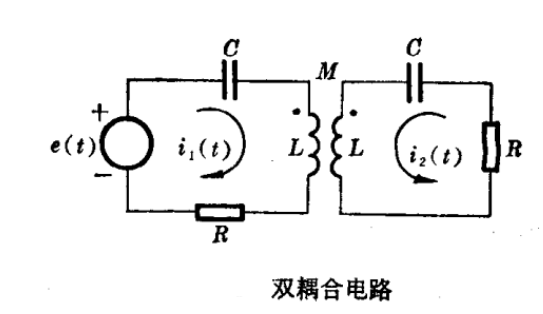
例如,对于图中所示的双耦合电路,可以列出一对微分方程:
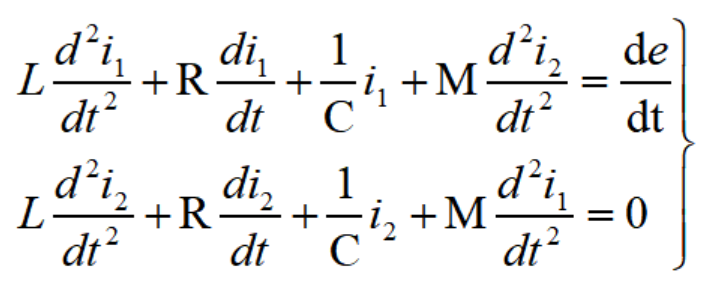
用消元法来求解这两个联立的二阶微分方程时,就会导得一个四阶的微分方程。例如其中消去i1,即可得
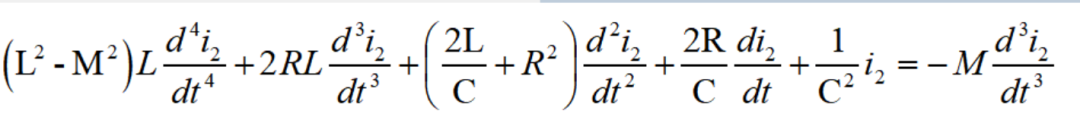
由此推广到一般,对于一个线性系统,其激励函数与响应函数、或者输入函数与输出函数之间的关系,总可以用下列形式的微分方程式——输入-输出方程来描述:
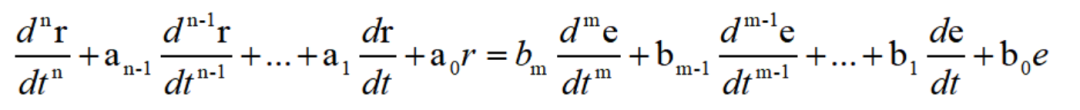
这个式子是一个常系数的n解线性常微分方程,在做线性系统的分析时,就必须要求解这个微分方程。
在高等数学中,这个微分方程式的解包括两个组成部分:一是此方程相应的齐次方程(令该式右边为零所得的方程)的通解,另一是满足此非齐次方程的一个特解。
齐次方程的通解为n个指数项之和,其中包含有n个未定常数,需要用n个初始条件确定。作为系统的响应来说,通解的这部分就是自由响应。
非齐次方程的特解,要根据方程右边函数即系统的激励函数的具体形式来求解,作为系统的响应来说,特解的这部分就是受迫响应。
对于一个可以用低阶微分方程描述的系统,如果激励信号又是直流、正弦或者指数之类的简单形式的函数,那么用上述古典的求解微分方程的方法去分析线性系统是很方便的。但是,如果激励信号是某种较为复杂的函数时,求方程的特解就不那么容易了。特别是当系统又须用高阶微分方程描述时,利用古典法求解微分方程的工作将变得格外困难。
正是避免这种困难,人们找到了利用变换域的方法去求解微分方程并分析系统。在上世纪四、五十年代以前,对于较为复杂的系统的分析,几乎无一例外地采用拉普拉斯变换法。
然而,应用拉普拉斯变换法以避免古典法遇到的困难,必须付出进行正反两次变换的代价。这个变换工作,有时并不轻松。特别是在工程技术中,常常会遇到激励函数是某一个数据的序列或是某一条曲线而无法表示为简明的解析式的情况,这样的函数当然也就难以对他进行变换了。这时拉普拉斯变换法也显得无能为力。
根据电路理论,系统的响应并不一定要划分为自由响应和受迫响应两个部分,而可以根据叠加加定理,把它分为仅由初始条件引起的零输入响应和仅由外加激励源引起的零状态响应两部分。
在求零输入响应时,只要求解上述齐次方程并利用初始条件确定解中的待定系数,这个工作无大困难。
在求零状态响应时,就是求解包含激励函数在内的初始条件为零的非齐次方程。
对于复杂信号激励的线性系统,在时域中求解系统的非齐次微分方程的解的另一条路子是应用叠加积分。正好像把激励信号在频域中分解成单元激励函数那样,激励信号也可以在时域中分解为脉冲信号或阶跃信号。
把这些单元激励分别加于系统并求出其响应,然后把这些响应叠加,即可得到复杂信号加于系统的零状态响应。基于这种思想所导得的叠加积分,就是卷积积分与杜阿美尔积分,而这两者之间,具有十分密切的关系。
编辑:jq
-
信号与系统中卷积分析和总结2021-09-29 43615
-
自动控制原理第三章_时域分析法_Part4部分2016-09-02 830
-
时域离散系统的基本网络结构与状态变量分析法2015-12-23 823
-
系统时域分析法中几个问题探讨2009-10-25 692
-
层次分析法2009-09-15 827
-
控制系统的时域分析法--线性系统的稳定性2009-07-27 5065
-
时域分析法2009-05-26 1800
-
控制系统的时域分析法2009-01-08 701
全部0条评论

快来发表一下你的评论吧 !

