微分方程的算子形式和拉普拉斯变换式之间的是什么关系？

一、什么是微分算子符号？

描述线性系统的激励函数和响应函数间关系的微分方程，具有以下形式：

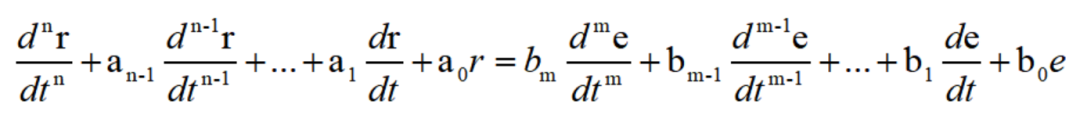
式中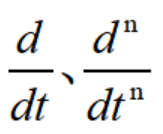为时域中的微分算子符号，当它们作用于某一时间函数时，该函数就要对时间变量t分别进行一次和n此微分运算。现在为了方便计算，

把微分算自符号用p来代表，即令：

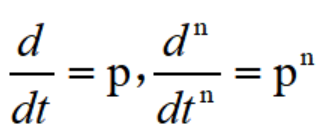
把积分算子用1/p来代表，即令：

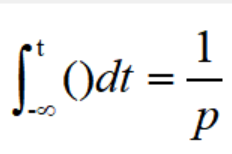
于是有：

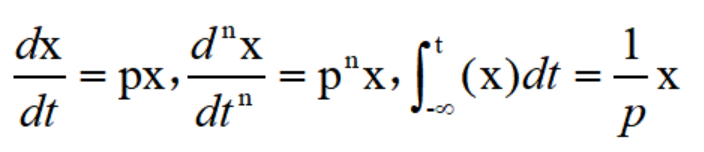
利用这样的符号，积分微分方程或微分方程就可以用较为简化的形式写出。

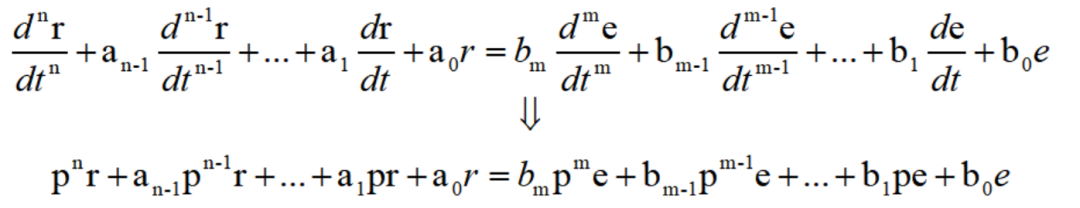
或者仿照代数方程把公共因子提出来的方法，还可以写成：

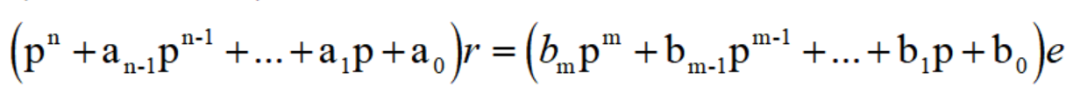
在这里，虽然把微分算子符号p像代数量那样处理，但是不要忘记它不是代数量。因此，例如

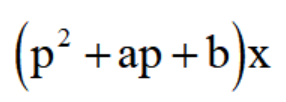
这样的式子中，

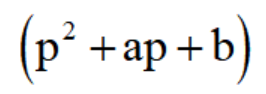
并不是用来与函数x相乘的代数量，而它作为一个整体，是一个作用在函数x的运算符号，代表着一定的运算过程，即

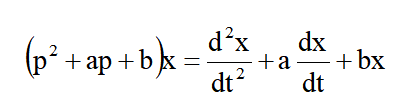
利用算子符号把微分方程写成代数方程的算子方程，于是就会自然地阐述这样的一个问题，即代数方程中的运算规则在算子方程中是否适用？

对于这个问题的回答是：一般适用，但有例外。

例如，在代数方程中有关系

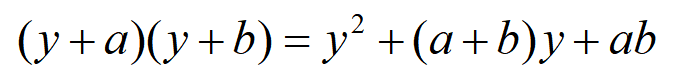
在算子方程中关系

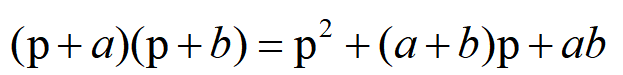
是否也成立呢？只要加以运算检验，就可以证明这关系是成立的。证明如下

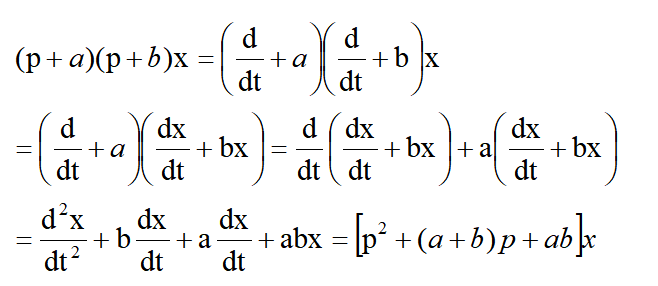
把这检验法加以推广，不难得出结论，即由p的多项式所组成运算符号可以像代数式那样进行相乘和那样因子分解。

再例如：

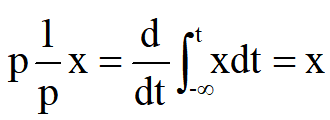
这里也像代数式中一样，分子分母中的p可以消去。但是

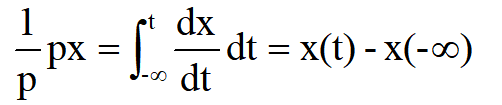
这里分母和分子中的p一般就不能消去。这表明

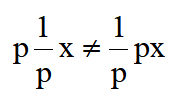
也就是说，微分和积分的运算次序不能任意颠倒，两种运算也不一定能抵消。同样，若将式

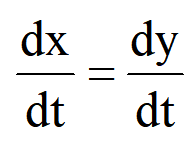
两边积分，可得：x=y+c

其中c为积分常数。由此可见，在等式px=py，双方的算子p一般也不好消去。

以上说明，代数量的运算规则对于算子符号一般也可以应用，只是在分子分母中或等式两边中相同的算子符号却不能随便消去。

二、微分方程的算子形式和拉普拉斯变换式之间的是什么关系？

描述系统的输入输出的微分方程一般形式有：

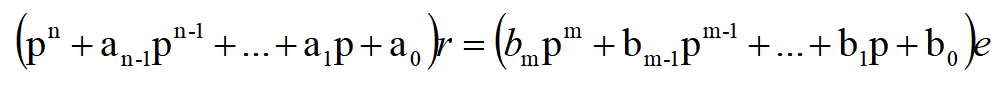
把左右两边p的多项式分别记为D(p)和N(P)，则有

D(p)r(t)=N(P)e(t)

这一微分方程又可进一步写成

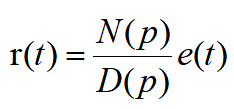
把p的分式N(p)/D(p)定义为转移算子H(p)，即H(p)=N(p)/D(p)

于是，在时域中响应函数与激励函数之间的关系，就可用以下简明的一般形式表示：r(t)=H(p)e(t)

当求系统的零输入响应时，激励函数e(t)为零，就要解齐次方程

D(p)r(t)=0

当求系统的零状态响应时，则要解非齐次方程

r(t)=H(p)e(t)

把微分方程的时域算子的形式与拉普拉斯的变换式相比较，将下式进行拉普拉斯变换，得

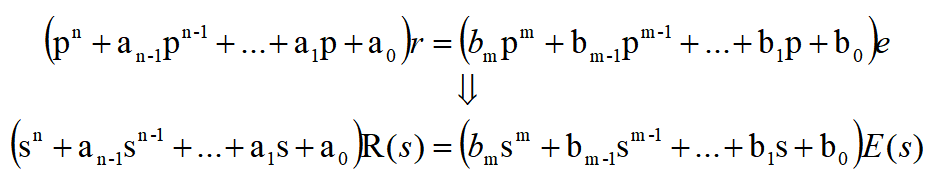
把此等式左边s得多项式记为D(s),右边s得多项式记为N(s)，则有

D(s)R(s)=N(s)E(s)

或者R(s)=N(s)E(s)/D(s)=H(s)E(s)

其中H(s)=N(s)/D(s)为在复频域中表示响应函数和激励函数之间关系的转移函数。

当求系统的零输入响应时，激励函数E(s)为零，D(s)R(s)=N(s)E(s)成为D(s)R(s)=0。系统的零输入响应由特征方程D(s)=0的根决定。

当求系统的零状态响应时，只要将式R(s)=N(s)E(s)/D(s)=H(s)E(s)进行拉普拉斯反变换即得。

把拉普拉斯的式子与算子形式的微分方程式相比较，就可以发现各对应得关系式之间，具有完全相似得形式。

可以看到，

在拉普拉斯变换式中，R(s)、E(s)、H(s)等都是复频率变量s的函数，H(s)E(s)即表示这两个函数相乘。

而在算子形式的微分方程中，r(t)、e(t)都是时间函数，H(p)是时域中的运算符号，H(p)e(t)并不表示两个函数相乘，而只表示对方程中的时间函数进行某种特定的运算。

算子形式的微分方程和其拉普拉斯变换式之间的相似性，很自然会引起人们提出这样的问题，即在求解系统的响应时，是否也具备同样的相似性？

或者说，能不能把拉普拉斯变换中的一套求解法搬过来用于时域中求解微分方程呢？

对于求系统的零输入响应，回答是肯定的。

但是对于求系统的零状态响应，除了两者均以叠加原理为共同基础外，在激励函数的分解和系统单元激励函数的响应等具体形式上，时域分析法就不同于复频率分析法，然而两种分析法之间，又存在着密切的关系。

编辑：jq