

全面介绍因果推断方向的基础方法
描述
写在前面
这一部分主要介绍的是因果推断方向的基础方法,后面会对这个方向前沿的论文和方向做一些基础介绍,这些论文和方法有些我进行了精读或者实现。
有些只是粗略地了解了大概的主旨,但是会力求讲解得尽量清楚明白,这里的介绍不分先后,只是对不同方法进行介绍,不同领域在早期和近期都有相关新论文出现,有任何问题和建议欢迎评论和私聊。
meta learning
这个方向使用基础的机器学习方法去首先Estimate the conditional mean outcome E[Y|X = x](CATE),然后 Derive the CATE estimator based on the difference of results obtained from step 1,我们常见的uplift model里面one model和two model方法其实也是属于meta learning,在这个领域one model方法是所谓的S-learner,two model方法是所谓的T-learner
T-learner & S-learner
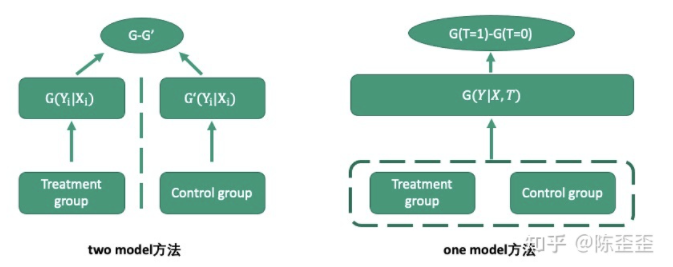
这里不多赘述这两种方法,简单来讲,T-learner就是用分别的两个base learner去模拟干预组的outcome和非干预组的outcome,优点在于能够很好地区分干预组和非干预组,缺点则在于容易出现两个模型的Bias方向不一致,形成误差累积。
使用时需要针对两个模型打分分布做一定校准,S-learner是将treatment作为特征,干预组和非干预组一起训练,解决了bias不一致的问题,但是如果本身X的high dimension可能会导致treatment丢失效果。而且这两种方法更偏向于naive的方法,很多其他的问题比如干预组和非干预组样本不均衡的问题、selection bias的问题都未解决。
2. X-learner
在这两种方法的基础之上还有《Metalearners for estimating heterogeneous treatment effects using machine learning pnas.org/content/116/10》这篇论文中介绍的X-learner
首先跟T-learner一样,用base learner去预估干预组和非干预组的response
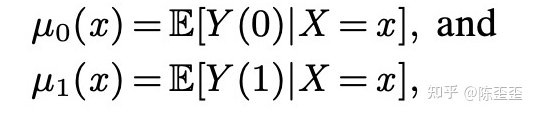
然后定义
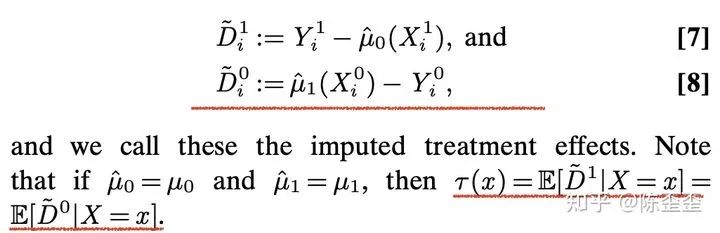
这里D的定义为response的预估值和实际值的差值,然后我们用一个estimator去预估这里的D,最终我们的CATE就是这两个预估出来的τ的加权和。

论文中用图来解释了这么做的原因,如下:
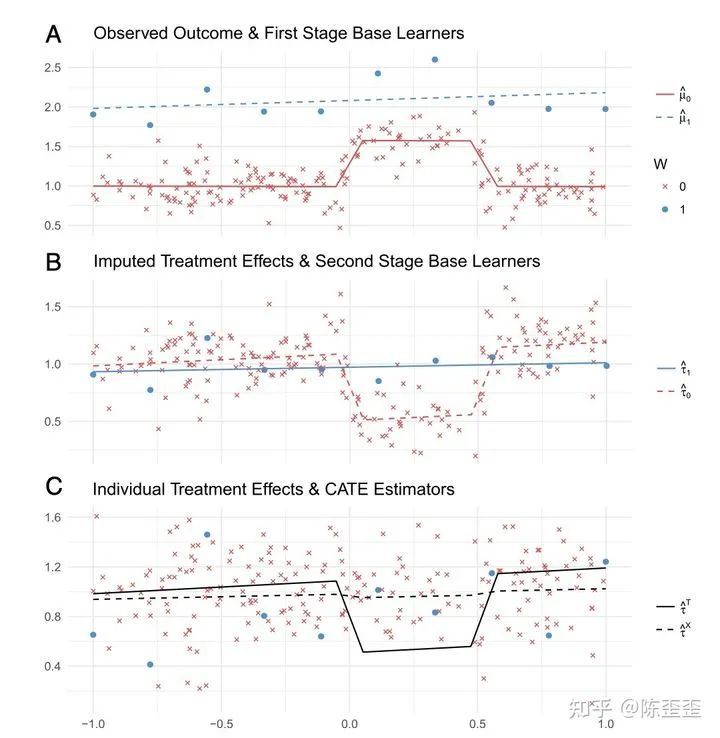
如上图所示,如果我们的干预组和非干预组样本数量不均衡,如图A的蓝色,那么在预估蓝色的base learner时会出现无法拟合到中间上凸部分的情况,最终得到的treatment effect就是在中间部分下凸的结果。
但是如果我们使用了imputed treatment effect,会得到C中虚线的均衡结果。
论文中还提到了自己的实验,实验效果总结来看,如果treat和不treat的数据量差别比较大的时候,X learner效果特别好,但是如果CATE接近0的时候,X learner效果不如S learner,比T learner好,make sense的。
3. 总结性论文
meta learning的方法有非常多,这里只是提到较为经典的三种,其他meta learning的方法比如R-learner有点老了,这里不再介绍,在《Transfer Learning for Estimating Causal Effects using Neural Networks arxiv.org/abs/1808.0780》中比较有意思的是提到了很多方法的方案。
包括传统艺能S-learner,T-learner,X-learner和比如warm start T-learner、joint training等等,有兴趣可以看看。
representation learning
表示学习对于因果推断其实算是非常自然的想法,本身由于selection bias的存在,导致treament group和control group的人群自带偏差,而类似S-learner的方法又会使得treat的作用丢失,那么将人群embedding中并尽可能消除bias和保存treat的作用就非常重要了。
BNN & BLR
比较经典的论文有BNN、BLR《Learning Representations for Counterfactual Inference arxiv.org/abs/1605.0366》,整体的算法如图:

其中B指的是loss:
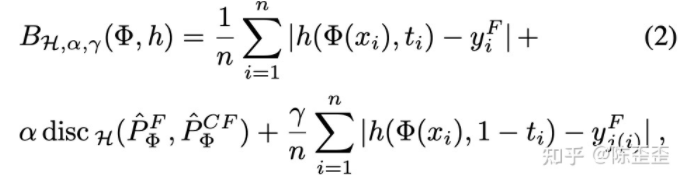
loss包含了三部分:事实数据的误差+和与i最近的j的反事实数据的误差和事实数据+反事实数据的分布差异,那我们是怎么学习φ的呢?
一个方法是对于特征进行选择BLR,在embedding层只有一层,更加白盒,相当于特征筛选,只保留在treatment group和control group差距较小的特征。

另一个方法是深度的方法BNN,embedding后整体的loss加入分布的差异。
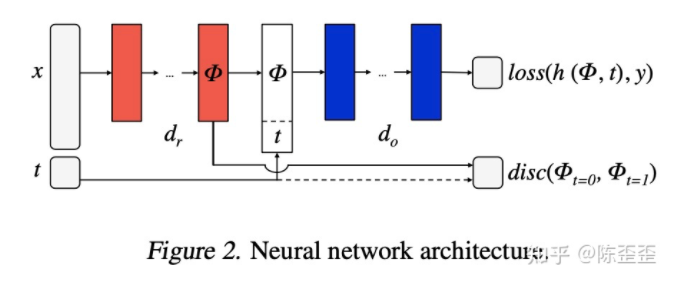
2. TARNet
与这篇论文很相似的论文包括TARNet《Estimating individual treatment effect:generalization bounds and algorithms arxiv.org/abs/1606.0397》,这篇文章整体的思路跟BNN那篇有点像,说到了BNN那篇的问题。
这里面讲了BLR的两个缺点,首先它需要一个两步的优化(优化φ和优化y),其次如果如果φ的维度很高的话,t的重要性会被忽略掉,挺有道理的,但感觉跟那篇唯一的区别就是解决了一下treat和control组的sample数量不均衡的问题,所以火速看了一下就过了
loss的计算为:

可以看出是在上篇论文的基础上增加了ω的加权,去除了样本不均衡的问题。整体的算法步骤如下:

把两步走的优化变为了同时优化,虽然优化看起来比较微小,但如果大家实际跑一下IHDP数据集的话会发现提升还是挺明显的。
3. CFR
还有一篇论文是在TARNet之上进行优化的,《Counter Factual Regression with Importance Sampling Weights https://www.ijcai.org/Proceedings/2019/0815.pdf》而本文的改进点也在ω上,不除以p(t),而是用一个网络学习了p(t|x),除以p(t|x)
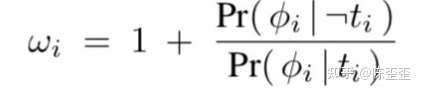
作者将其简化为
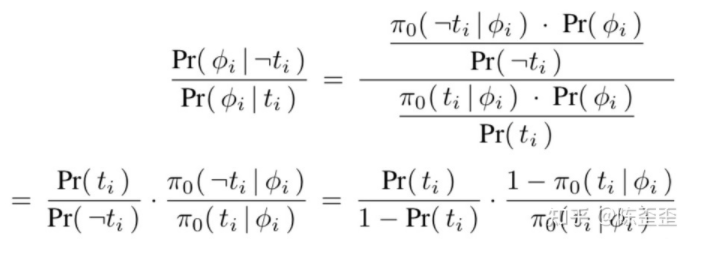
可以用任何的网络去拟合第二项,整体的过程为:

4. ACE
还有一篇论文讲到了另一个角度《Adaptively Similarity-preserved Representation Learning for Individual Treatment Effect Estimation cs.virginia.edu/~mh6ck/》
这篇主要的思想希望在representation之后能够尽可能地保留local similarity,用一个toy example来说如下:
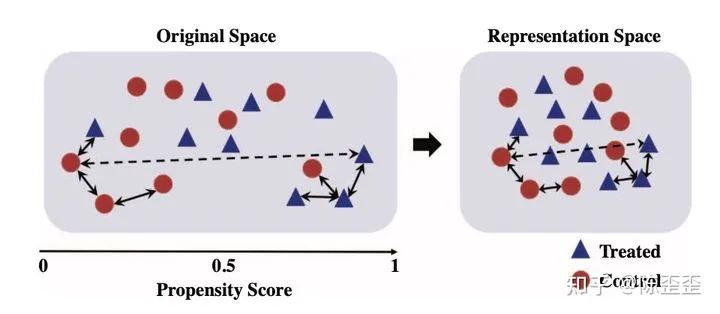
整体的框架如图:fprop(x)是提前训练好的倾向性得分function
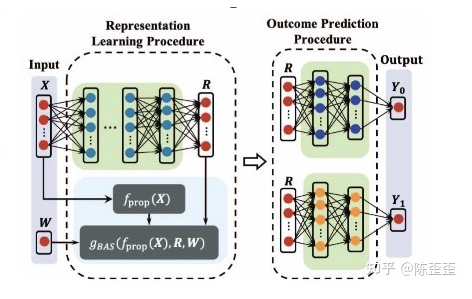
整体希望representation之前用x计算出倾向性得分相近的两个个体,representation之后,representation之间的距离还是相近,把最重要的部分贴下来如下:

其中Q是Ri和Rj的联合概率(R是representation),P是xi和xj的联合概率,similarity preserving loss就是Q和P的KL散度,其中S的函数如下:
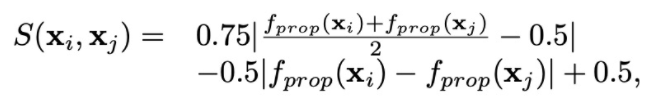
整体的loss包括正常的imbalance loss:
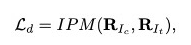
Factual y的分类或者回归loss:
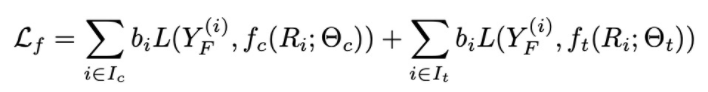
还有similarity preserving loss,总的loss function就是:
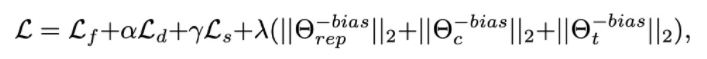
5. SITE
还有一篇比较类似思想的论文是SITE《Representation Learning for Treatment Effect Estimation from Observational Data papers.nips.cc/paper/75》但这篇论文我没有非常认真地读,来自NIPS,也是非常经典的一篇,说的主要是普通的representation learning的方法考虑了全局的分布信息。
但是没有考虑用户间的局部相似性,然后KNN的方法考虑了局部相似性,但是忽略了全局信息,这里面用了三元triplet pairs的方法选择三个对,用的是倾向性得分,倾向性得分在中间的一对,倾向性得分接近1的treat unit,倾向性得分接近0的control group,有兴趣的同学可以自己看一下。
编辑:jq
-
 cdl111
2022-10-13
0 回复 举报好棒 收起回复
cdl111
2022-10-13
0 回复 举报好棒 收起回复
-
使用因果图设计测试用例2010-09-03 538
-
典型因果推断CCI算法在无线网络性能中应用优化2017-12-13 1100
-
基于加性噪声的缺失数据因果推断2018-01-14 631
-
基于用户生成内容的位置推断方法2018-01-21 560
-
Xilinx如何实现AI推断2019-06-01 1418
-
数据测试用例设计:因果图方法2020-06-29 3520
-
一种基于粗糙集聚类的报文格式推断方法2021-04-25 788
-
超详细EMNLP2020 因果推断2021-05-19 5899
-
基于深度神经网络的因果形式语音增强方法2021-06-10 818
-
基于e-CARE的因果推理相关任务2022-05-16 1985
-
基于马尔科夫边界发现的因果特征选择算法综述2022-07-29 1833
-
具有Event-Argument相关性的事件因果关系提取方法2023-02-02 1886
-
ChatGPT是一个好的因果推理器吗?2024-01-03 1480
-
当系统闹脾气:用「因果推断」哄稳技术的心2024-08-14 934
-
鉴源实验室·测试设计方法-因果图2024-11-05 924
全部0条评论

快来发表一下你的评论吧 !

