

关于神经网络的十大学习率衰减提效策略
描述
十大学习率衰减策略!
简 介
目前越来越多非结构化问题的出现,神经网络也扮演着愈加重要的作用。一个好的神经网络对于最终任务的预测至关重要,但要得到一个好的神经网络则需要考虑众多的因素,本文我们重点介绍神经网络中调参重学习率衰减的调节策略。本文介绍目前tensorflow中的9大学习率衰减策略。
exponential_decay = learning_rate_decay.exponential_decay
piecewise_constant = learning_rate_decay.piecewise_constant
polynomial_decay = learning_rate_decay.polynomial_decay
natural_exp_decay = learning_rate_decay.natural_exp_decay
inverse_time_decay = learning_rate_decay.inverse_time_decay
cosine_decay = learning_rate_decay.cosine_decay
cosine_decay_restarts = learning_rate_decay.cosine_decay_restarts
linear_cosine_decay = learning_rate_decay.linear_cosine_decay
noisy_linear_cosine_decay = learning_rate_decay.noisy_linear_cosine_decay
学习率衰减
01
分段常数衰减
在对应区间置中不同的学习率的常数值,一般初始学习率会大一些,后面越来越小,要根据样本量的大小设置区间的间隔大小,样本量越大,区间间隔要小一点。在真正的网络训练中,需要操作人员根据具体任务对学习率具体设置
该方法有助于针对不同任务进行精细地调参,在任意步长后下降任意数值的learning rate。
02
指数衰减
指数衰减的方式,学习率的大小和训练次数指数相关,指数衰减简单直接,收敛速度快,是最常用的学习率衰减方式,其数学公式为:
如下图所示,红色的为学习率随训练次数的指数衰减方式,蓝色的即为分段常数衰减 。
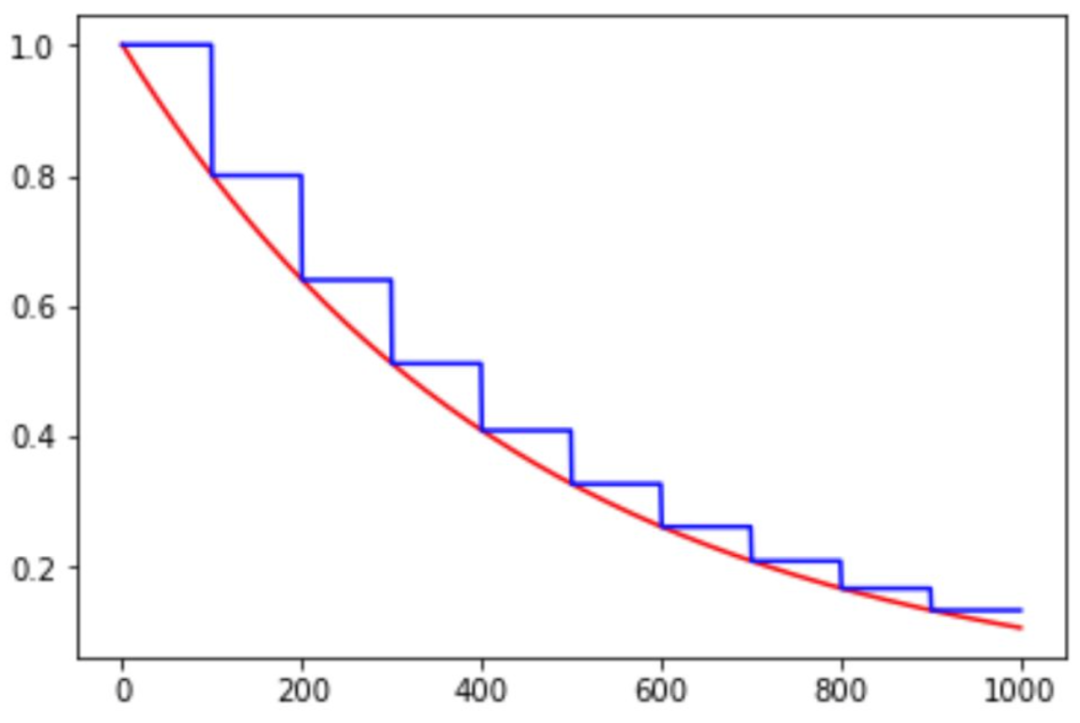
03
自然指数衰减
自然指数衰减和指数衰减方式相似,不同的在于它的衰减底数是,所以它的收敛的速度更快,一般用于相对比较容易训练的网络,便于较快的收敛,其更新公式为:
和分段常数以及指数衰减相比,其中绿色的是自然指数衰减。
04
多项式衰减
多项式衰减的方式进行更新学习率,需要给定初始学习率和最低学习率,然后按照给定的衰减方式将学习率从初始值衰减到最低值,其更新规则即为:
此处需要注意有两个机制:
降到最低学习率后,到训练结束可以一直使用最低学习率进行更新;
另一个是再次将学习率调高,使用decay_steps的倍数,取第一个大于global_steps的结果,即:
可以用它来防止神经网络在训练的后期由于学习率过小而导致的网络一直在某个局部最小值附近震荡,在后期增大学习率跳出局部极小值。
05
倒数衰减
倒数衰减的数学公式为:
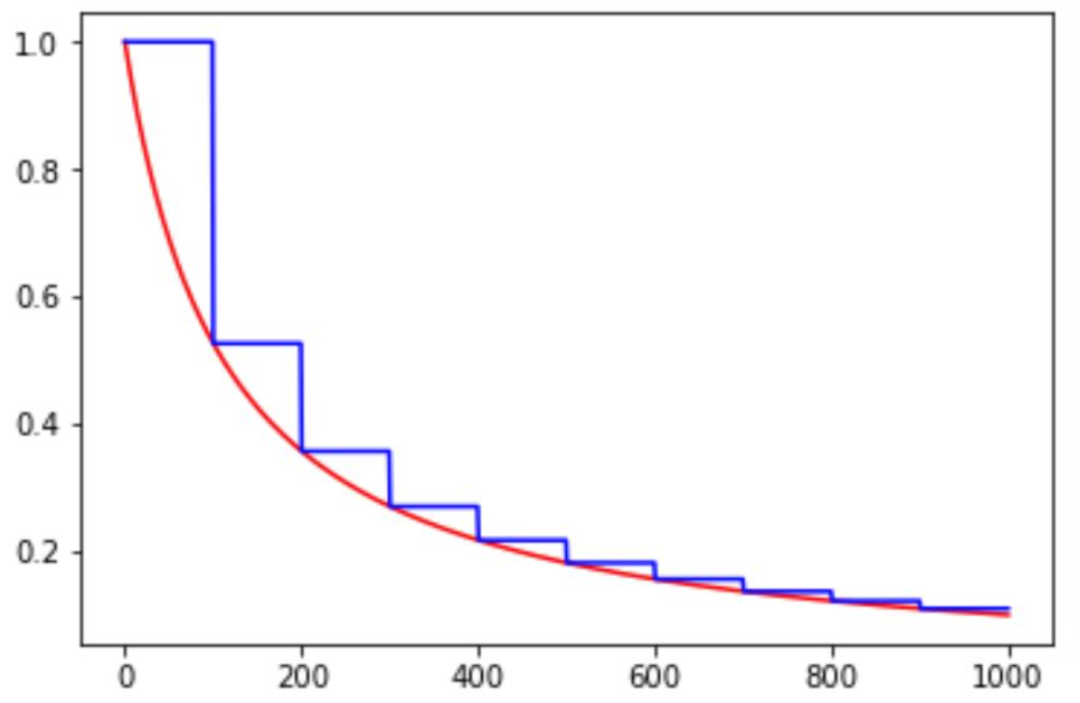
06
余弦衰减
顾名思义,就是采用余弦方式进行学习率的衰减。其更新机制如下:
其中alpha可以看作是baseline,保证学习率不会低于某个值。不同alpha的影响如下:
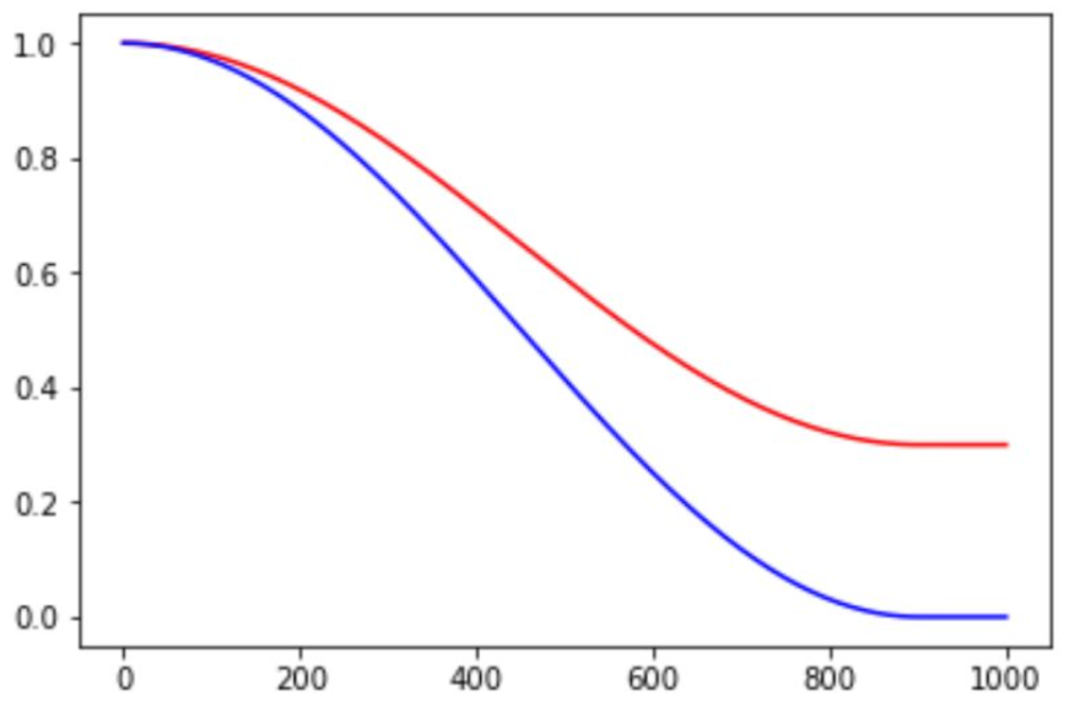
07
循环学习率衰减
学习率以循环周期进行衰减。是循环学习率的cycle版本。
余弦函数式的下降模拟了大lr找潜力区域然后小lr快速收敛的过程,加之restart带来的cycle效果,有涨1-2个点的可能。
08
线性余弦衰减
线性余弦衰减方式是基于余弦方式的衰减策略,其数学公式为:
线性余弦衰减一般应用领域是增强学习领域,
09
噪声线性余弦衰减
在线性余弦衰减的基础上,加入了噪声。就得到了噪声线性余弦衰减。噪声线性余弦衰减提升了学习率寻找最优值的随机性和可能性。
0110
自定义学习率
大家还可以依据自己的想法自定义学习率衰减策略,例如可以依据验证集合的表现,来更新学习率,如果验证集合上评估指标在不断变好,则保持lr,否则降低学习率。
参考文献
tensorflow learning schedule之分段常数衰减用法
An Overview of Deep Learning Optimization Methods and Learning Rate Attenuation Methods
Tensorflow中learning rate decay的奇技淫巧
TensorFlow使用记录 (三):Learning Rate Scheduling
深度学习中的固定学习率衰减策略总结
https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/training/learning_rate_decay.py
编辑:jq
-
BP神经网络与深度学习的关系2025-02-12 1487
-
详解深度学习、神经网络与卷积神经网络的应用2024-01-11 3470
-
什么是神经网络?什么是卷积神经网络?2023-02-23 4822
-
卷积神经网络模型发展及应用2022-08-02 13208
-
基于BP神经网络的PID控制2021-09-07 2587
-
神经网络与神经网络控制的学习课件免费下载2021-01-20 1515
-
【AI学习】第3篇--人工神经网络2020-11-05 4122
-
【案例分享】ART神经网络与SOM神经网络2019-07-21 3180
-
神经网络资料2019-05-16 3319
-
如何估算深度神经网络的最优学习率(附代码教程)2017-12-07 2662
-
labview BP神经网络的实现2017-02-22 14181
-
神经网络教程(李亚非)2012-03-20 56687
-
MATLAB神经网络工具箱函数2009-09-22 4133
-
神经网络PID控制策略及其Matlab仿真研究2009-09-14 559
全部0条评论

快来发表一下你的评论吧 !

