解读目标检测中的框位置优化

目标检测已经有了长足的发展，总体来说根据阶段个数，可以划分为Two-stage（Faster RCNN）、one-stage（SSD） 或者E2E（DETR）。根据是否基于anchor先验，可以划分为anchor-based（Faster RCNN）、anchor-free（CornerNet）的方法。

本文主要从目标框位置优化的角度来介绍目标检测领域的相关工作。框位置优化主要可以分为以下几个方面

By XYWH，这是指通过优化与ground truth的中心点坐标值、宽和高的值来实现目标框位置的优化

By keypoint，这是指通过优化关键点的方式来找到目标框的位置

By LRBT，这是指通过优化与ground truth 四条边之间的距离的方式来实现目标框位置的优化

By IoU，这是指通过最大化与GT计算得到的IoU来优化目标框的位置

uncertainty，解决目标检测框真值的边界不确定性

01

Optimize by XYWH

定义

优化目标为预测bbox的中心点坐标（x，y）和宽高（width， height）与对应真值的差距尽可能的小。接下来我们以Faster RCNN为例介绍该方法 。

思路

基于Anchor的先验，我们可以得知每个proposal的大概位置。考虑到利用Anchor的先验信息，作者使得预测框到anchor的距离和与子匹配的GT框到anchor的距离尽可能的相似。距离：XYWH的差值。

匹配方法

1、 代表 和 的IoU值; 大于指定阈值，代表i和j之间具有匹配关系

2、 对应最大IoU的 ;如第一步j没有得到任何匹配，则在此步，i和j具备匹配关系

优化公式

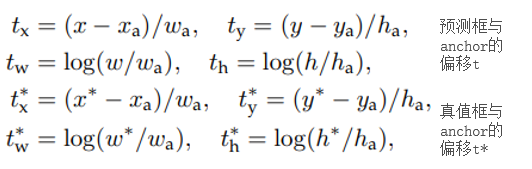
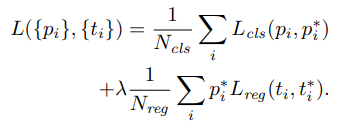
上述是Faster RCNN的优化目标函数，我们的目标就是让 尽可能的逼近 ，之间的优化函数 可以选择L2，or L1 作者这里使用了Smooth L1

Q&A

为什么是SmoothL1？

A： smooth L1 在 x 较小时，对 x 的梯度也会变小，而在 x 很大时，对 x 的梯度的绝对值达到上限 1，也不会太大以至于破坏网络参数。smooth L1 可以避开 L1 和 L2 损失的缺陷。

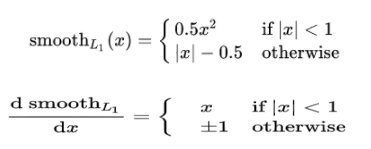
为什么要除 ？

A： 消除不同anchor大小带来的影响，相当于归一化为什么w和h的优化要以log的形式进行？

A： target（H和W）是学习一个放缩的尺度，因此尺度值需要大于0，因此需要使用exp，对应的这里为log函数

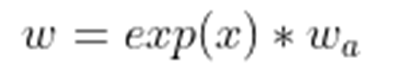
02

Optimize by Keypoint

定义

优化目标为找到物体的两个关键点：左上点和右下点。核心为一个semantic segmentation问题。

接下来我们以Corner Net为例介绍该方法 。

思路

不同于基于Anchor的方法，本方法需要先识别关键点在图中的位置。由于在pooling过程中会引入左边的误差，所以需要再针对每个关键点预测一个offset。

Q&A

如何训练和预测关键点？一个点一个pixel

A：作者使用2D Gaussian来生成，如下图所示，针对每个pixel，生成一个半径大小为r的圆形Gaussian分布。半径r的大小是自适应的。

若一个pixel对应了多个Gaussian分布的值，选择最大的。如何根据top-left和bottom-right关键点两两组合形成最终的bbox？

A：作者提出针对每个keypoint 预测一个embedded vector，当top_left和bottom_left的embedded vector相似度大于一定阈值的时候则认为他们是描述的同一个bbox。则形成一个bboxkeypoint往往落在物体的外部，对应位置的特征可能不能很好表征物体，会增加识别关键点的难度。

A：作者提出了CornerPooling

优化公式

综上所述，在该方式中，我们需要以下三个优化目标

1、关键点的分类，可以看成一个语义分割任务，作者采用了focal loss的变种，如下图所示

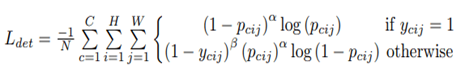
2、每个关键点的offset预测，每个关键点offset的真值如下式所示。作者采用smooth l1去优化

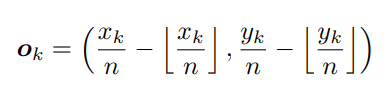
3、每个关键点的embedded vector预测，作者使用下式来优化embedded vector。让属于同一个物体的vector相似，不属于同一个物体的不相似

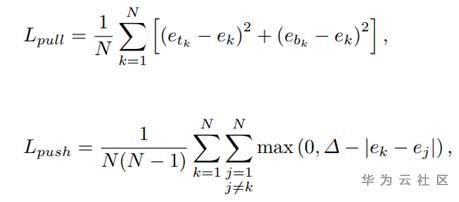
整体训练&推理流程

03

Optimize by LRBT上述基于关键点回归的方法有几个缺点

1、容易产生ghost bbox，这是由于tl br的embedded 相似度的确较高产生的

2、后处理的时候，若关键点较多，复杂度较高。为K^2的复杂度。

为了解决该问题，作者提出了基于LRBT的优化方式

定义

优化目标为物体的“中心点”距离四条边的距离

接下来我们以FCOS为例介绍该方法 。

思路

在feature map上找到每个“中心点”，针对每个中心点预测和他对应的框的四个值。

Q&A

1、如何定义“中心点”

A：我们需要找到特征图上每个location（pixel）和gt_bbox的匹配关系，然后将匹配到的gt_bbox作为真值。

匹配关系：

- location落在某个gt_bbox内部，这里的落在内部可以直接的理解为落在内部，也可以替换成其他规则。例如真实中心的某个范围。

- 为了加速收敛，l、r、t、b应该在某一个范围内，如果不在这个范围内，就以为着应该由其他location来优化。例如，都应该在scale_factor的范围内2、如何解决一个物体框可能包括了多个“中心点”

可以支持这种1对多的关系，一个物体框有多个中心点负责预测，后续通过NMS消除。

但是每个中心点的权重作者认为是不一样的，因为距离物体实际中心近的中心点其难度较低，应该就越准确，所有在NMS的时候权重应该高。所以作者多了一个branch来预测centerness，即用于评估每个中心点的难易程度。

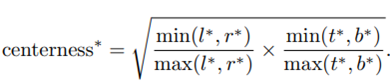
3、如何解决一个中心点可能落在多个物体框内部

作者选择面积最小的bbox作为优化目标，其实也可以优化多个？

04

Optimize by IoU上述基本都是基于距离的回归，但是我们最终的评价指标是IoU，所以我们优化的目标和我们最终评价的指标之间还存在一些差异。在下面的case中，第一行所有情况的L2loss都是一样的，但是IoU和GIoU是存在一定差异的。在第二行中，L1 Loss都是一样的，但是IoU 和 GIoU 也是不一样的。

为了解决上述的差异，作者提出了使用IoU作为我们的优化目标

定义

优化目标为使得预测框和真值框IoU最大，使用IoU 作为损失函数主要有以下两个优势1. 优化目标和评价指标存在差异，Ln（L2， L1）范式优化和IoU优化并不完全等价，如上图所示。2. IoU对目标物体的scale不敏感。但是直接使用IoU Loss也存在如下两个问题1. IoU值容易为0，且始终无法优化。2. IoU无法辨识不同方式的对齐，比如方向不一致。为了解决上述问题，作者提出了GIoU General IoU Loss

GIoU

定义公式如下所示，C是包含A和B的最小box。当IoU（A， B）为0的时候，优化目标转化为让C与AUB之间的空隙尽可能小。即就是A和B尽可能靠近。

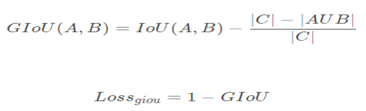
A = np.random.random（［N， 4］）B = np.random.random（［N， 4］）C = np.zero_like（A）C［：， ：2］ = np.min（A［：， ：2］， B［：， ：2］）C［：， 2：］ = np.max（A［：， 2：］， B［：， 2：］）

实验结果如下所示

DIoU

Motivation

Distance IoU Loss 主要是为了解决如下两个问题

GIoU倾向得到一个较大的bbox

GIoU 区分两个对象之间的对齐方式比较间接，仅通过引入C的方式来反应重叠的方式，不够直接。如下图所示。第二幅图展示来当GIoU一样的情况下，DIoU是不一致的（前提是，中心点重合的情况下认为拟合的最好）。

Contributions

提出了基于IoU Loss的一般性范式，这是我认为最大的贡献

提出了DIoU Loss，在IoU loss的基础上将central之间的距离作为惩罚项

在各个数据集和detector上都取得了不错的效果

Detail

范式：作为认为IoU loss应该优化的目标包括三个方面

两个框之间的重合度

中心点之间的距离

长宽比的相似性

作者基于上述的1&&2，提出了DIoU Loss，结合1&&2&&3提出了CIoU Loss（C is complete）

DIoU：定义如下所示，其中关键中心点之间距离的惩罚项的分子代表两个框中心点之间的欧式距离。分母是GIoU中矩阵C的对角线变长。分母起到了归一化的作用。

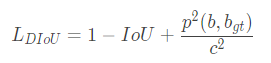
CIoU的定义如下所示，它在DIoU的基础上增加了对长宽比的惩罚项

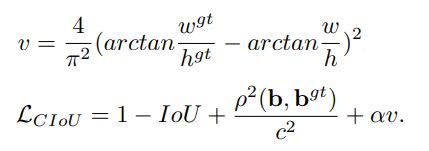
05

Optimize by uncertainty

Motivation

不一致性

训练和测试两个阶段的，如上图所示，训练的时候单独优化classification score和IoU score，测试的时候将其相乘，然后会导致训练和测试的时候不一致。

测试的时候，进入NMS的是classification score乘IoU score，就会存在一种情况classification score较低，但是IoU score较高，然后使得负样本没有被过滤。这是因为IoU score并没有对负样本做优化，所有负样本的IoU score并不受控制，如下图所示。

Localization Quality Estimation （LQE） 是许多one-stage或者anchor-free方法改善效果的途径。

但是上述的方法会带来一定的不一致性1，它主要包括以下两点

Contribution1为了解决上述的问题，作者提出使用Joint的方式来联合优化classification score和IoU score。即就是用同一个prediction值即代表classification score又代表IoU score

不灵活性

目前目标检测的标准框有时候会存在标注的不确定性（或噪声）。而目前常用的bbox优化方式是优化Dirac分布（具体什么是Dirac分布后续会介绍）。

但是Dirac分布过于固定，不能解决uncertain的问题，因此有人提出了Gaussian 分布。

但是作者认为Gaussian分布过于理想，不能适应于复杂的现实情况。

Contribution2因此，作者提出了不依赖于任何先验的潜在分布优化（underlying distribution）

Method

Quality Focal Loss

在上一节，我们介绍了作者使用同一个prediction score来同时表示classification score和IoU score，那么优化该值的时候真值应该是什么呢？作者选择IoU值作为优化的真值，由于IoU是一个［0，1］之间的连续值。而传统的focal loss优化的目标是{0， 1}这样的离散值。因此该loss更加泛化一点（general）

Quality Focal Loss就是上述的更加泛化的FocalLoss，其定义如下所示

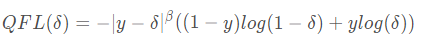
上述公式的后部分是展开形式的交叉熵，系数是adaptive的，当预测是和真值接近的时候，系数小，当远的时候系数大。

Distribution Focal Loss

在本节我们主要介绍以下何为Distribution，以及我们的Distribution Focal Loss。

先看为什么是Distribution？传统的BBox regression即就是直接优化两个值，让pred_w接近真值的w。

换个角度看，假设我们预测的值为pred_w， 我们直接优化pred_w接近w，那么我们就相当于让pred_w出现的概率是1.0。这即就是Dirac Distribution。

也就是说我们最终的预测值是对所有y可能出现的值计算积分。也就如下公式所示。

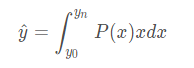
接下来在看我们的Distribution Focal Loss， 有上式可知，上式是比Dirac更加泛化的形式。因此本文用上式来计算预测的y^。预测y^之前我们需要先清楚两点

连续值的积分是不好实现的，我们可以用离散值的求和来代替

我们需要确定预测值的范围。

有了上述两个条件，我们可以得到pred^的计算公式如下所示。

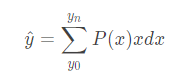
得到上述的y的预测值后，我们如何去优化呢？因为我们知道y^是接近y的，因此我们需要让int（y）和int（y）+1的prob最大。因此就可以对应下面的公式。

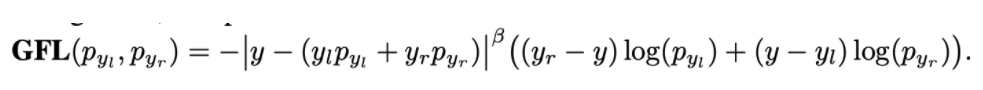
Discussion

GIoU 是否必须？

根据总的Loss定义，我们发现GIoU貌似不是必须，因为通过

distribution focal loss也可以起到bbox优化的目的。因此我们做了对比实验，发现取消GIoU loss会带来小幅度的指标下降。

别的应用场景

数据分类（带有噪声）。针对每个类，我们将其拆分成N份（0.， 0.1， 0.2， …， 1.0），分别预测每一份的概率，然后求和，即为最终该类别的概率。

distribution的意义

分布越陡峭，证明越确定，否则越不确定。

本文分享自华为云社区《目标检测中的框位置优化总结》

原文作者：卖猪肉的阿漆 侵删

地址：https://bbs.huaweicloud.com/blogs/263436

编辑：jq