同步解调技术背后的基本思想是什么

有时，我们需要测量低频信号。例如，考虑在压力变化非常缓慢的应用中使用的压力传感器。

我们测量的信号几乎是直流电，但这会如何影响我们的设计？

我们知道在高频下，事情会变得疯狂，我们需要仔细注意设计的每一个细节。这可能会误导我们错误地认为测量低频信号是一项微不足道的工作。我们将看到情况并非一定如此。事实上，有一种称为同步解调的技术，它有意增加工作频率以实现更准确的测量。

低频测量示例

在某些应用中，直接测量具有低频输出的传感器（不应用同步解调）。例如，驻极体麦克风是一种特殊类型的可变电容，可以直接测量。驻极体麦克风的电容随气压变化（声波）而变化。

电容器结构中使用了一种称为驻极体的 Teflon 类材料，其表面结合有固定电荷。由于电容器上的电荷是固定的，由气压变化引起的电容值的变化会导致电容器两端的电压发生相应的变化（对于电容器，我们有 Q=CV）。

如图 1 所示，驻极体麦克风通常有一个内部 JFET，用作缓冲器。

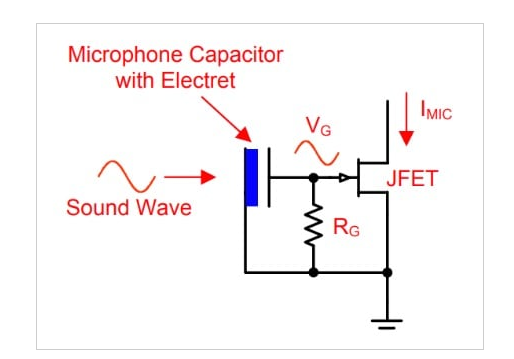
在此特定应用中，传感器（麦克风）产生的信号直接应用于电路的放大元件。这种测量电容传感器的方法有时被称为“直接直流”方法，因为直接测量电容器上的低频信号。

我们测量低频信号时出现的主要问题之一是闪烁噪声。

闪烁噪声

闪烁噪声的平均功率与工作频率成反比（这就是闪烁噪声也称为 1/f 噪声的原因）。因此，信号频率越低，我们必须处理的噪声功率就越大。图 2 显示了精密运算放大器ADA4622-2的电压噪声频谱密度。

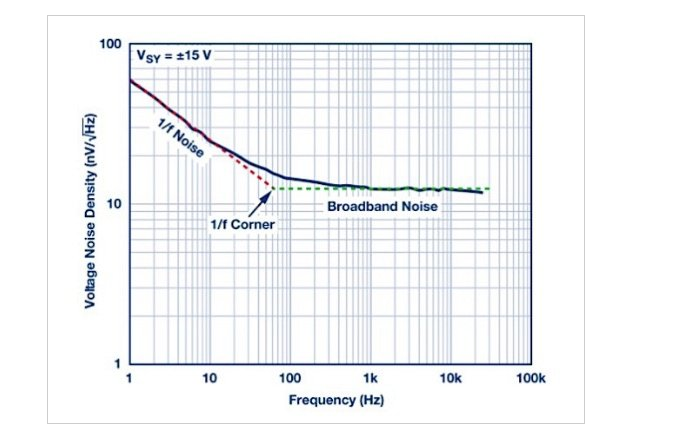
在大约 100 Hz 以上，噪声功率几乎均匀分布在不同频率之间。噪声曲线的该区域对应于器件的热噪声。然而，当我们移至低于 100 Hz 的频率时，由于闪烁噪声，噪声平均功率会增加。

用直线近似噪声分布的两个不同区域，我们可以找到一个交点，称为 1/f 噪声角频率（如图 2 所示）。转角频率允许我们确定给定频率下设备的主要噪声类型（闪烁或热）。

在 1/f 转角频率以下，传感器产生的小信号可能完全被噪声掩盖。如果我们能以某种方式将传感器输出信号的频率增加到转角频率以上，我们就可以进行更准确的测量。这是同步解调技术背后的基本思想。

图 3 显示了在更高频率下进行测量如何将所需信号从设备闪烁噪声中提取出来。

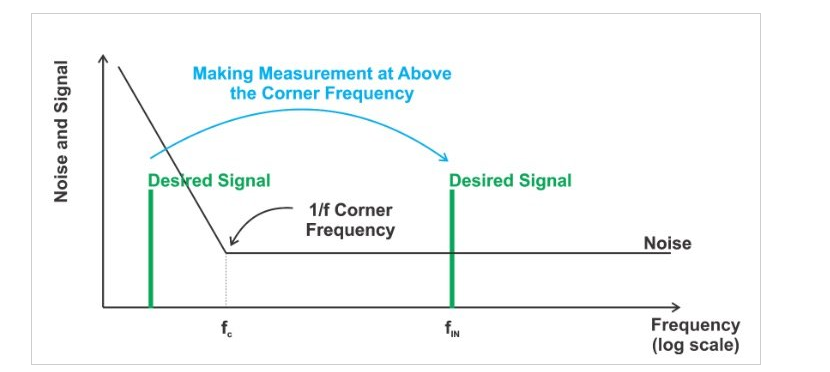
图 3

对于图 1 所示的“直接直流”测量，闪烁噪声可能不是一个严重的问题，因为语音信号在非常低的频率（低于约 20 Hz）下显示的功率可以忽略不计。此外，我们或许能够定制内部缓冲晶体管以降低其 1/f 转角频率。

然而，在某些应用中，传感器的输出信号频率要低得多（几乎是直流），我们需要更准确的测量。在这种情况下，电子元件的闪烁噪声可以完全掩盖传感器产生的信号，我们需要同步解调等技术来规避闪烁噪声问题。

传感器的交流激励

图 4 说明了使用交流信号测量电容传感器的情况。在该图中，可变电容 C sense模拟了我们的电容传感器。输入电压源施加频率在 1 kHz-1 MHz 范围内的正弦波。根据 C sense与 C 2的比率，电压信号出现在运算放大器的输入端。在这种情况下，可以选择运算放大器的输入信号，使其充分大于电路的 1/f 转角频率。这与“直接直流”方法形成对比，在这种方法中，测量信号可能处于非常低的频率。

由于所需信号远离 1/f 转角频率（如图 5 所示），因此闪烁噪声不是限制因素，我们可以检测到小得多的信号。

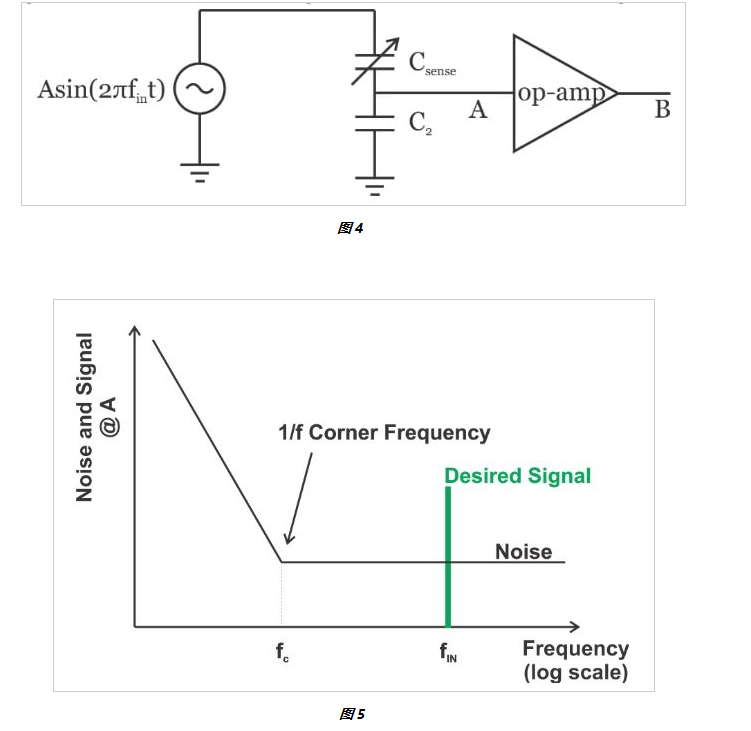
在运算放大器输出端，我们有一个放大的信号，可用于确定可变电容的值；然而，我们需要一个带通滤波器 （BPF） 来抑制噪声成分并仅保留所需信号。这在图 6 中进行了描述。

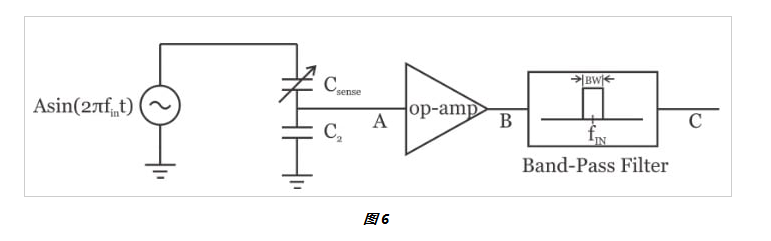
请注意，BPF 的中心频率与输入频率相同。假设带通滤波器是理想的，我们将获得所需信号以及落在带通滤波器通带内的热噪声（下图 7）。

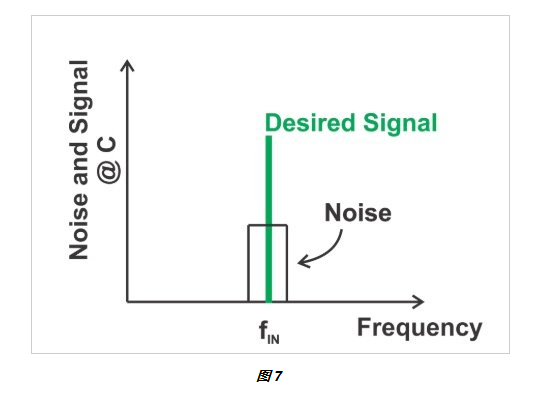
使用 BPF 的限制

在图 6 中，我们需要一个高 Q 带通滤波器来充分抑制噪声并保持所需信号。一个非常高 Q 值的滤波器可以让我们拒绝大部分噪声。但是，存在两个主要问题：首先，实现高 Q 连续时间带通滤波器可能具有挑战性，尤其是在高频下。事实上，随着滤波器中心频率的增加，实现给定的 Q 因子变得越来越困难。这是因为在高频（大约几百 MHz）下，运算放大器的放大能力有限，并且表现出非理想的相位响应。您可能会说图 6 中滤波器的中心频率在 1 kHz-1 MHz 范围内，这并不是真正的高频滤波器。嗯，你说得对，我们可以在这个频率范围内有一个高 Q 滤波器。然而，随着频率越来越高，我们必须消耗更多的能量。换句话说，对于给定的 Q 因子，我们期望较低频率的滤波器表现出较低的功耗。因此，如果可以在较低的频率下执行运算放大器之后的滤波，则功率效率会更高。

图 6 所示概念的第二个问题是调谐带通滤波器的中心频率。请注意，模拟连续时间滤波器的中心频率取决于电阻器、电容器和跨导体的值。这些参数的绝对值可能会有很大差异。因此，滤波器的中心频率可能不完全在 f IN. 由于滤波器具有较窄的通带，由于滤波器中心频率的变化，所需信号很容易落在滤波器通带之外。使用高 Q BPF 的第二个问题可能比上一段中讨论的功率效率问题更具挑战性。有趣的是，如果应用需要高 Q 连续时间带通滤波器，我们必须采用一种机制来调谐滤波器中心频率。例如，一些集成带通滤波器应用使用一个在概念上类似于锁相环的反馈环来调谐滤波器中心频率。然而，这样的系统对于读取传感器来说似乎过于复杂和耗电。在下一节中，我们将看到巧妙的调整可以使用低通滤波器而不是 BPF 来实现所需的滤波操作。通过这种方式，我们可以拥有一个不需要任何频率调谐电路的低功耗解决方案。

同步解调

同步解调的概念如图 8 所示。在该图中，乘法器放置在运算放大器之后。

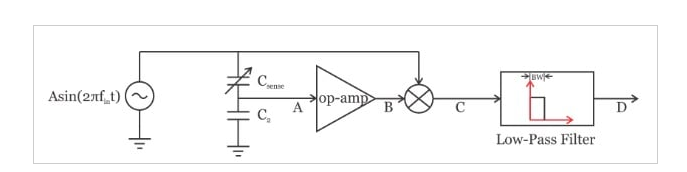
假设运放输出的输出信号为 v乙（吨）=乙秒一世n（2πF一世n吨+φ）v乙（吨）=乙秒一世n（2πF一世n吨+φ）。 该信号乘以输入信号一种秒一世n（2πF一世n吨）一种秒一世n（2πF一世n吨） 这给出了：

vC（吨）=一种秒一世n（2πF一世n吨）×乙秒一世n（2πF一世n吨+φ）=12一种乙C○秒（φ）-12一种乙C○秒（4πF一世n吨+φ）vC（吨）=一种秒一世n（2πF一世n吨）×乙秒一世n（2πF一世n吨+φ）=12一种乙C○秒（φ）-12一种乙C○秒（4πF一世n吨+φ）

第一项是直流，但第二项是输入频率的两倍。因此，窄低通滤波器可以去除第二项，我们有：

vD（吨）=12一种乙C○秒（φ）vD（吨）=12一种乙C○秒（φ）

如果我们假设运算放大器没有引入任何延迟，即 φ=0φ=0， 我们获得 vD（吨）=12一种乙vD（吨）=12一种乙。 如您所见，低通滤波器的输出与节点 A 处的信号幅度成正比，可用于测量C秒电子n秒电子C秒电子n秒电子。 上述方法具有三个优点：

可以选择传感器输出的频率，使其充分高于 1/f 转角频率。

滤波器以尽可能低的频率运行，并应消耗尽可能小的功率。

该滤波器不需要频率调谐电路。

在本系列的下一篇文章中，我们将继续讨论并仔细研究同步解调技术的实现。

结论

“直接直流”方法直接测量电容传感器产生的低频信号。由于闪烁噪声，这种低频测量的精度可能会受到限制。为了规避这个问题，我们可以使用交流信号来激励传感器。由于测量发生在高于 1/f 转角频率的频率上，因此闪烁噪声不再是限制因素。在这种情况下，我们可以使用带通滤波器来选择所需的信号；然而，使用高 Q 带通滤波器可能具有挑战性。相反，我们可以同步解调被测信号并使用低通滤波器来执行所需的滤波。
责任编辑人：CC