失调电压变化是如何影响电路性能的

在本文中，我们将通过探索一个 LTspice 电路来继续讨论，该电路可以帮助我们预测失调电压变化将如何影响电路性能。

分析失调电压分布

这是我在上一篇文章末尾展示的 LTspice 原理图：

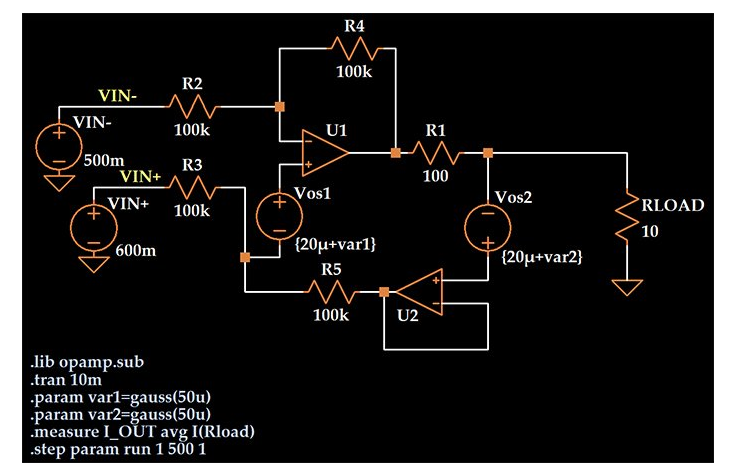
我通过添加一个与每个运算放大器的同相输入端子串联的电压源，将偏移电压加入到电路中。

我想创建一个类似于 AD8606 精密运算放大器报告的分布的失调电压分布，为此，我为 Vos1 和 Vos2 指定了 20 μV 的典型值，并向该典型值添加了一个高斯变量。

传递给gauss函数的参数是标准偏差，因此我创建了两个直流电压源，其值根据正态分布随机变化，平均值为 20 μV，标准偏差为 50 μV。

我们需要确认 LTspice 产生的分布与 AD8606 测得的失调电压分布一致。为此，我将模拟电路，绘制 Vos1 值，将它们保存到文件中，将它们导入 Excel，然后检查直方图。

请注意，在下面的示意图中，我更改了“.measure”语句，以便它记录 Vos1 的值而不是负载电流。

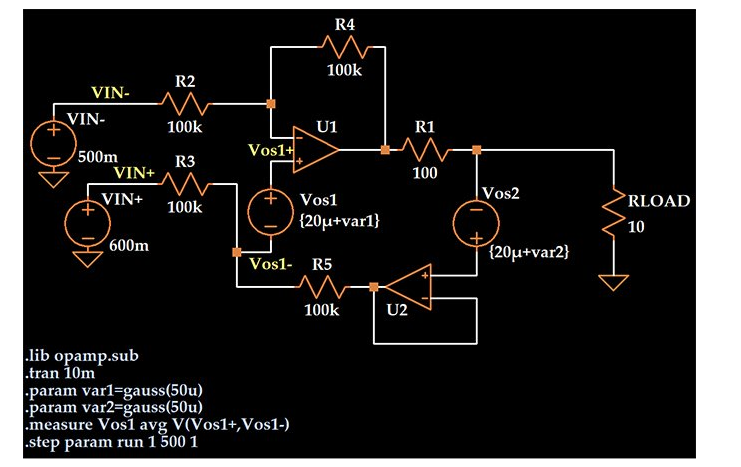
如果我打开 SPICE 错误日志，右键单击并选择“Plot .step‘d .meas data”，我会得到以下图：

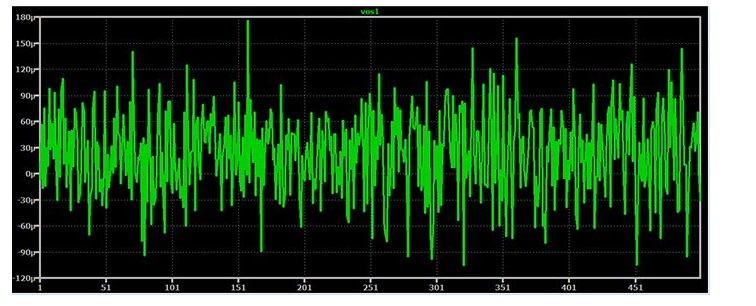
生成直方图

我现在可以通过右键单击并选择“文件”-》“将数据导出为文本”来保存这些数据。我将此数据导入 Excel，我有 500 个不同的偏移电压值：

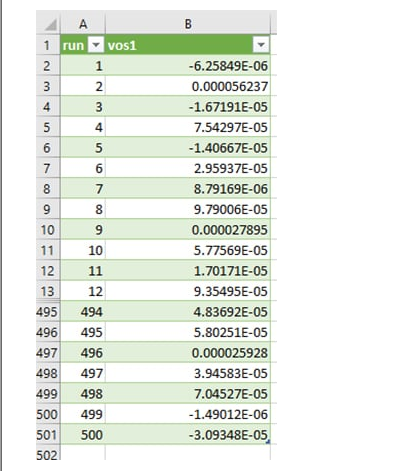
首先，让我们检查均值和标准差，以确保它们与应有的值相似，即 20 μV 和 50 μV。

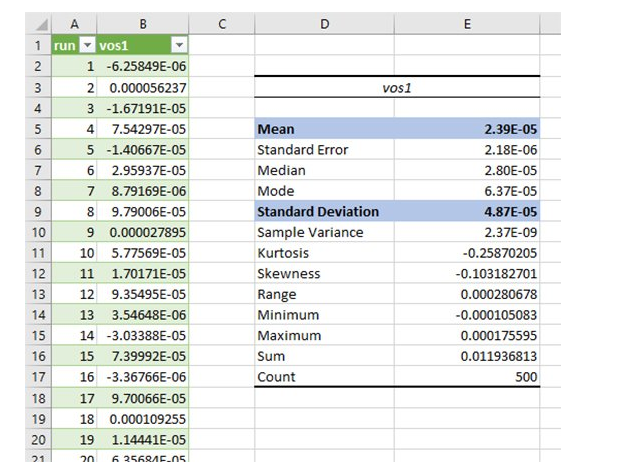
这很好；平均值为 23.9 μV，标准偏差为 48.7 μV。如果模拟包含大量运行，实际值将更接近预期值。例如，运行 4000 次时，平均值为 20.8 μV，标准偏差为 50.6 μV。

现在让我们看一下直方图：

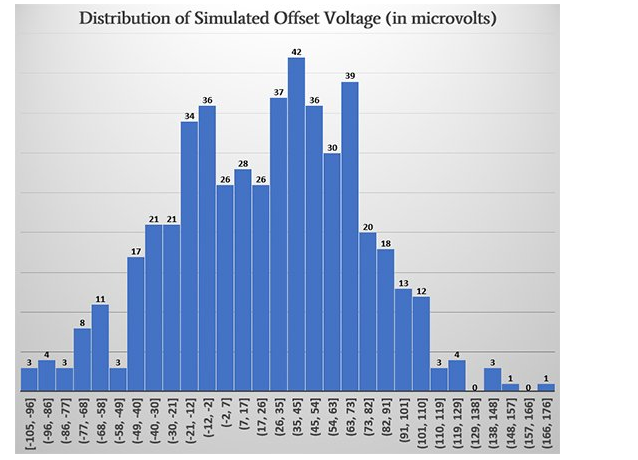
样本大小为 500 时，我们肯定不会得到完美的正态分布，但是当我将基本特征与 AD8606 分布（如下所示）的特征进行比较时，我很满意。

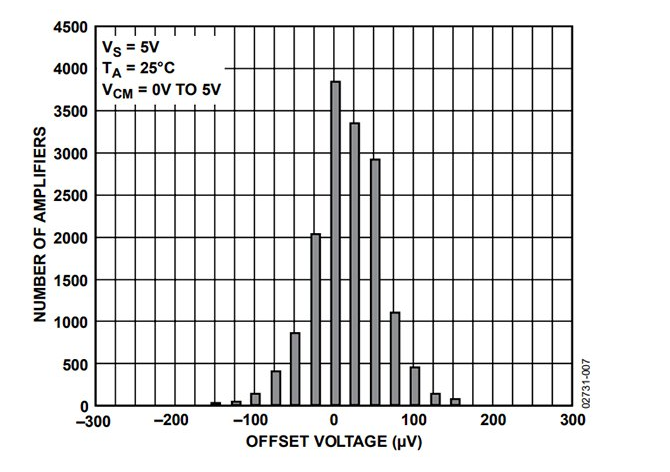
绘图取自 AD8606 数据表。图片由ADI 公司提供

仿真结果

在执行模拟之前，我将“.measure”语句恢复到其原始状态，即“.measure I_OUT avg I（Rload）”。预期负载电流为 1 mA。我首先在 Vos1 和 Vos2 源设置为零的情况下运行模拟；以下是 500 次运行的模拟负载电流值：

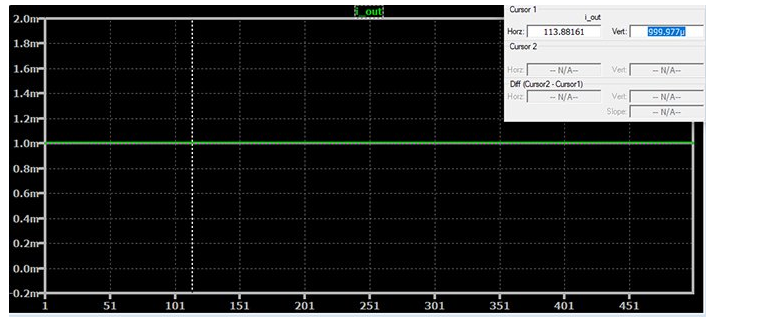
每次运行的负载电流都相同，这并不奇怪，因为没有参数发生变化，因此每次运行都具有完全相同的电路。我们还观察到运算放大器组件中内置了某种非理想行为，因为模拟负载电流为 999.977 μA 而不是 1 mA。所以我们从负方向的 23 nA 误差开始。

以下是包含偏移电压行为时的结果：

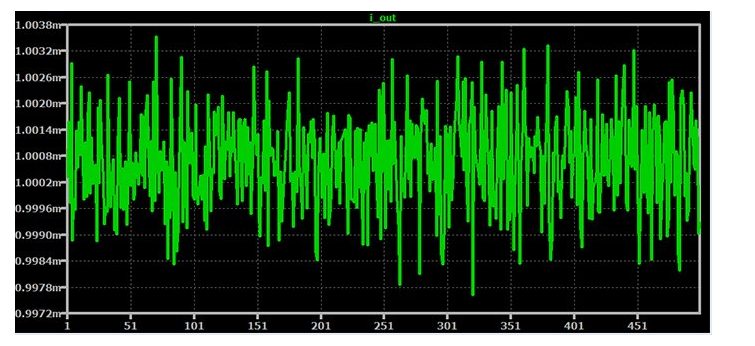
我们可以从初步检查中看出，影响并不是灾难性的。平均输出电流略有变化，我们与平均值的最大偏差约为 3 μA。

Excel 中的分析表明平均输出电流为 1.00068 mA。在最坏情况下的误差（相对于1mA的理论值）为3.5μA在正方向和2.4μA在负方向。

这些绝对是很小的误差，但它们对电路中的整体误差的贡献并不小，尤其是当我们将它们与电阻容差和温度的影响进行比较时：

在之前的一篇文章中，我们通过将所有电阻器置于 0.1% 的容差范围内并将工作温度从 –40°C 改变到 +125°C，产生了大约 +5 μA/–10 μA 的最大偏差。仅偏移电压就产生了 +3.5 μA/–2.4 μA 的最大偏差。

我们还必须记住，AD8606 的失调电压性能非常好。目前生产的许多运算放大器具有比 AD8606 更高的失调电压。

结论

我们使用直流电压源和 LTspice 的高斯函数来模拟运算放大器的输入失调电压对压控电流源精度的影响。我们看到，即使电路是围绕用于高精度应用的运算放大器构建的，偏移电压对整体输出误差的贡献很小但不可忽略。
责任编辑人：CC