简述FPGA的图像高斯滤波

在知乎上看到一个比较有意思的话题，卷积为什么叫”卷“积？哈哈哈哈哈

其中有个动图用卷毛巾生动形象的比喻了卷积的过程。

带着好奇心先看一下我们最熟悉的卷积公式：

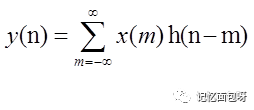
还可以改写成：

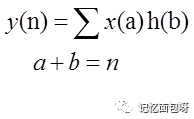
其中a，b表示a+b=n这条直线上所有的点。y（n）就表示这条直线上所有点对应的函数值x（a）h（b）的累加。

以下图卷毛巾为例，将毛巾沿红色虚线方向卷起来，设这条红色虚线为a+b=5，卷起来后这条红线上的所有函数值都累加到n=5这一点上，即是y（5）的值。

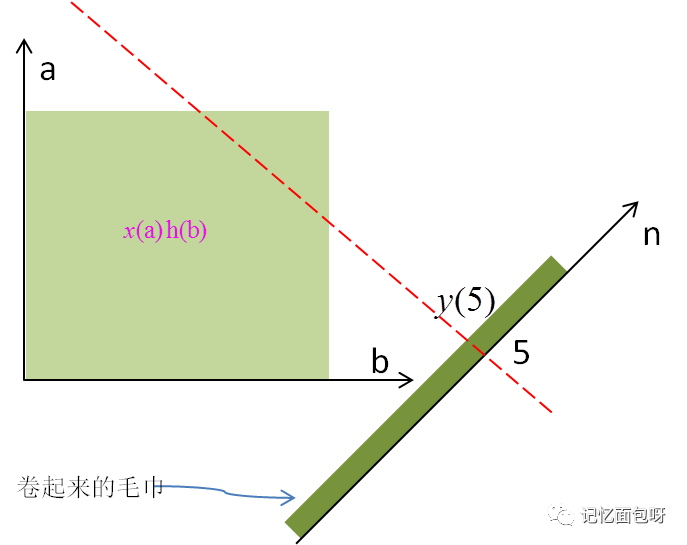
1.一维信号的卷积

上面只是从数学公式解释了卷积是如何计算的，但卷积物理意义是什么呢？

学习信号与系统的时候总是听老师说信号经过一个系统就是与这个系统进行卷积。所以我们先从一维信号来解释一下。

（1）表示信号δ（t）经过某系统产生了输出h（t）。

（2）将信号δ（t）延时τ后，输出也延时了τ，为h（t-τ）。

（3）将1，2中信号叠加输入系统后，产生输出y（t）也进行了一个叠加，输出等于h（t）+h（t-τ）。

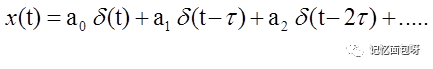
再假如有这样一个x（t），由很多个δ（t）组成，这个δ（t）不正是冲激函数嘛。它经过系统会输出什么？

由δ（t）冲激函数的性质

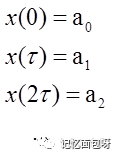
带入便得到了卷积公式。

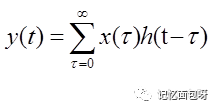
所以卷积的意义就是累加呗，得到的结果y（t）就表示在t这点的冲激响应和t之前所有冲激响应的”余波“的累加值。（这里累加下限τ=0是因为假设t《0时没有信号的，不会对t这点产生影响）

 

2.二维图像卷积

上升到二维空间，卷积公式变为

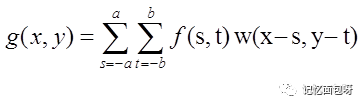
以高斯滤波为例，w（x，y）是二维高斯函数。

图像f与w卷积，可以同样理解为图像经过系统w所产生的输出，而图像中每个像素点可以理解为一维卷积中的信号δ（t），最终的输出也是每个像素点冲激响应累加的结果。

累加的上下标a，b代表着能对中心像素产生影响的周围像素的范围，而影响的大小取决于①它对中心像素的“余波”；②周围像素点本身的像素值（相当于一维中的a0，a1 ，a2 。 。 。 。）。

举个例子，当a，b都为2时，表示以某像素为中心3×3的矩阵内，所有像素都对此像素有影响。

想象一下这个3×3的矩阵中每个像素上都对高斯滤波器产生了冲激响应，可以想象成每个像素上有座山，山坡会延伸到周围像素上，山的高度可以叠加，那中心点像素的山就是最高的了。

那中间山的高度是多少呢？ 取决于：

①周围像素对中心像素的“余波”；

f（x-1，y-1）在中心像素的“余波”为1，f（x-1，y）在中心像素的“余波”为2，f（x-1，y+1）在中心像素的“余波”为1，f（x，y-1）在中心像素的“余波”为2，f（x，y）自己贡献了4，f（x，y+1）在中心像素的“余波”为2，f（x+1，y-1）在中心像素的“余波”为1，f（x+1，y）在中心像素的“余波”为2，f（x+1，y+1） 在中心像素的“余波”为1。

②周围像素点本身的像素值

最终山的高度等于∑（某点像素值 × 其对中心点”余波“）。而“余波”不就是所用的模板吗。

还有一点需要注意，这个模板并不是我们的w，而是将w翻转了180度，方便与相同位置像素对应。

由卷积公式得下式，对应图中相同颜色的相乘。

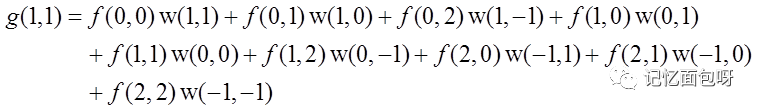
3.FPGA实现

理解了高斯滤波模板的意义，接下来就考虑如何用FPGA来实现了。由于图像是一个像素一个像素流入FPGA的，所以怎样将一个个像素流变成3×3的方块与我们的模板相乘是一个问题。

还好altera ip核中有个shift_ram，可以将数据缓存后分行输出。下图就比较直观的展现了它的功能。

所以我们需要将数据缓存两行，每行640个像素，加上当前流入的像素，就可以构成需要的3×3的矩阵了。

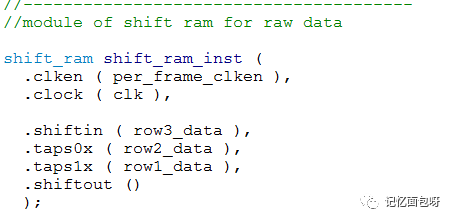
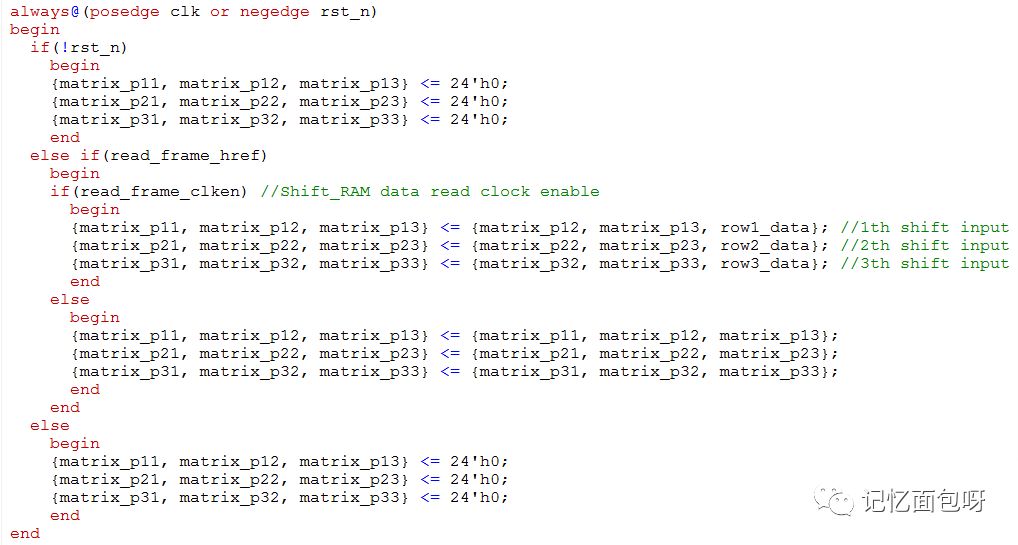
最后行场同步需要打两拍是由于输入数据的时候数据打了一拍，上图构建矩阵时打了一拍，详见完整代码。

仿真结果

可以看出shift_ram在缓存两行数据后，就可以三行数据同时输出。就可以构成3×3的矩阵了。

接下来对这个3×3矩阵进行乘上对应系数再累加，便得到滤波后的像素啦。

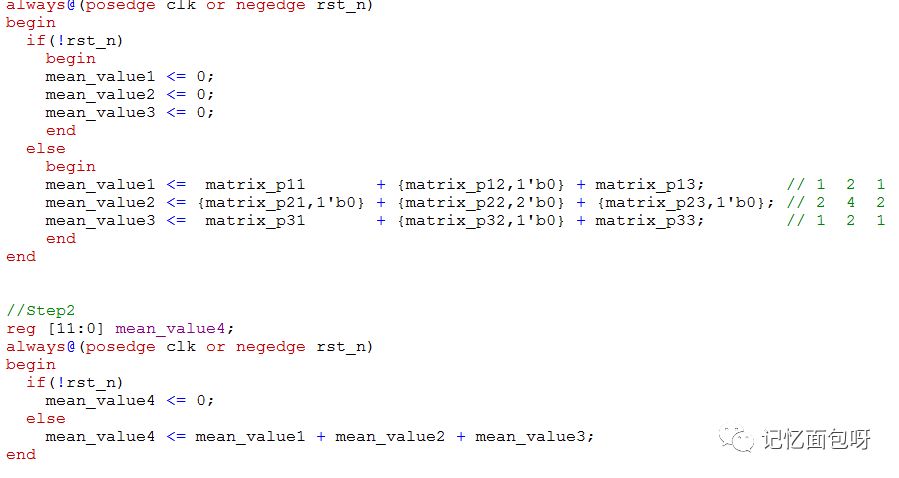
编辑：jq