如何使用相位噪声图方向时钟器件特性及适用应用场景

作者：安森美半导体 Brijesh Shah

每隔几年，几乎所有市场上广泛普及的高频串行通信标准（PCI-Express、USB、以太网、同步光网络（SONET）、串行ATA（SATA）、Infiniband等）都会被修订，以更好应对如今数据饥渴型社会的更高期望。随着这些标准新版本的推出，市场对支持它们的电子电路的需求也加强了。集成在当代系统应用中的高性能时钟产生及分配器件使用频域参数，也就是相位噪声和相位抖动来描述它们的性能。本文探讨相位噪声图怎样配合估计制造商数据表上没有明确提及的时钟器件特性，使工程师能够更好地评判针对特定应用的适合情况。

当应用高速串行链路时，可以利用周期抖动来推导相关位误差率（BER）。时钟器件的抖动传递及PLL带宽也是重要衡量标准，因为透过这些参数有可能更好推测输入源或输入时钟会怎样影响器件的输出。所有这些都将帮助工程师选择符合他们需求的恰当时钟器件。然而，这些参数很少直接标明，故必须进行计算。

抖动传递

抖动传递揭示一定偏移频率范围内的衰减量或产生的噪声。它由锁相环（PLL）的环路滤波器响应来确定。相位噪声图提供所有偏移频率时的噪声密度，因此它包含确定时钟器件抖动传递所必要的数据。显示抖动传递、产生及衰减的最佳方式，是使用在较低偏移频率时拥有较高底噪及在较高偏移频率时拥有较低底噪的时钟源。在低频时，PLL将高源噪声传递至输出；而在高频时，它将显示固有底噪，这是PLL低通带宽特性的缘故。

低带宽PLL即使在较低偏移频率时也能衰减抖动，PLL带宽越低，在此等频率时的衰减性能也会更高。然而，低带宽PLL存在响应时间较慢的缺点——它会花费时间来跟踪输入时钟变化。大多数网络通信链路在较低偏移频率时的约束不那么严格。

PLL带宽

如果使用了恰当的参考时钟源，除了抖动传递，相位噪声图也能帮助确定PLL带宽。为了充分理解PLL带宽估计及PLL的抖动传递，应当进行简单的测量设置，使用两个不同时钟源来为一个高性能零延迟缓冲器（ZDB）馈送信号。

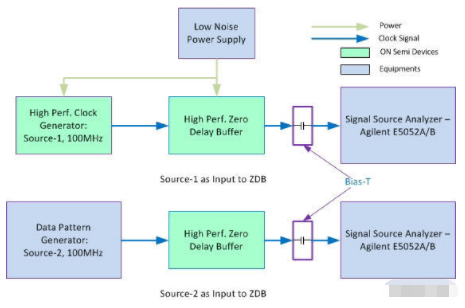
图1：电路图显示了PLL带宽及抖动传递测量

图1显示了介绍相位噪声测量设置的简单电路图。测量是使用安捷伦5052A信号源分析仪进行的。源1（高性能时钟产生器）和ZDB采用低噪声电源供电。

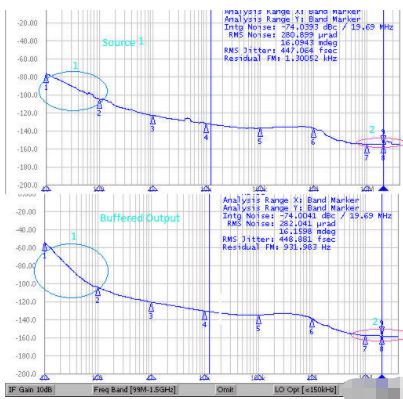
图2：源1及缓冲器输出的相位噪声图

如图2所示，源1的均方根（RMS）相位抖动为约447 fs，而缓冲器输出为约448.8 fs。RMS抖动是在从10 kHz至20 MHz的偏移频率范围内测量的。在10至100 Hz的较低偏移频率时，缓冲器噪声相比源而言较高，但对大多数通信信道而言这并不构成问题，因为它被PLL轻易地跟踪。输出缓冲器相位噪声图大致匹配高达1 MHz的源相位噪声图。高于此频率时，缓冲器输出的底噪低于源底噪，如图2中的第2号圈所示。

源2使用了数据模式产生器（DPG）。它拥有比源1量多高的底噪。因此，图3所示的缓冲器输出图匹配较低频率（10-100Hz）时的输入源。缓冲器-PLL传递低于1 MHz的输入噪声；源噪声图中30 kHz附近的突兀变化反射在缓冲器输出噪声图中，如图3中所第1号圈所示。对于高于1 MHz的频率而言，缓冲器底噪明显低于源底噪，如图3中2号圈所示；这表示缓冲器在此频率范围内充当抖动衰减器。

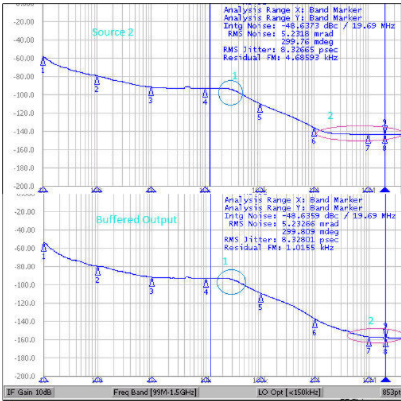
图3：源2及缓冲输出的相位噪声图

周期抖动

如前所述，周期抖动是用于在高速串行标准中对BER进行近似估算的一项重要参数，但通常情况下时钟器件制造商仅提供使用低噪声频域设备测量的相位抖动或相位噪声数据。相位噪声频谱定义为基于载波功率频谱密度峰值的衰减（单位为dB/Hz）。相位噪声频谱密度与RMS周期抖动之间的关系是：

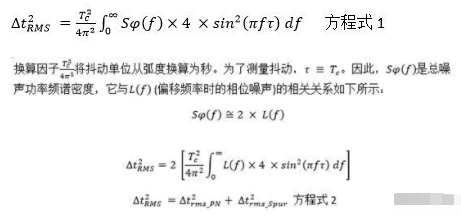
为了根据相位噪声图估计周期抖动，偏移频率的相位噪声必须乘以〖4sin〗^2 （πfτ）函数。dB换算4〖sin〗^2 （πfτ）显示它拥有-20dB/十倍频（decade）的斜率（见图5）。4〖sin〗^2 （πfτ）以dB为单位的值可以增加到相位噪声图数据中，单位为dBc。相关偏移频率范围内最终数据的数值积分将提供单边频带的相位噪声密度。例如，为了根据图4中给出的相位噪声图来估计周期抖动，增加以dB为单位的4 〖sin〗^2 （πfτ）函数数据到相位噪声（PN）数据（单位为dBc/Hz）中，如图5所示。所获得的蓝色曲线显示了相位噪声频谱密度。

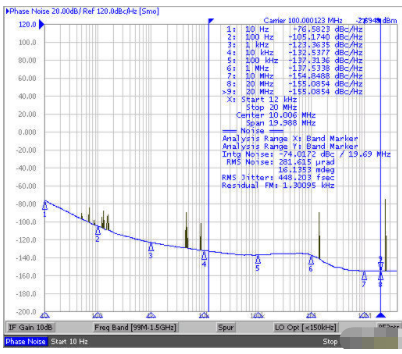
图4：带有毛刺的时钟产生器输出相位噪声图

对图5中蓝色曲线以下区域进行积分将得到相位噪声频谱密度（单位为dB）（对应区域A）。它可以使用下列方程式换算为均方根拉动：

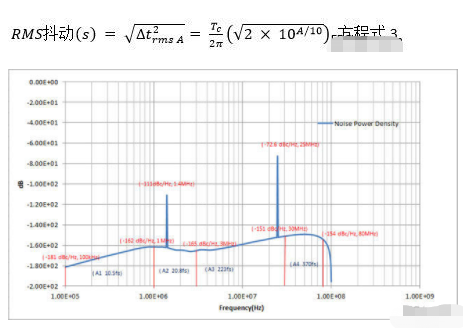
图6：相位噪声的RMS抖动换算

如图6所示，曲线下面的区域根据曲线形状或是使用分段线性函数，可以划分为几个不同部分（A1、A2等）。由于较低偏移频率噪声不会大幅影响周期抖动，故仅考虑较高偏移频率下的曲线。为了提高精度，完整曲线可以划分为多个部分，相应各个部分对周期抖动的影响。图6中的曲线划分为4个部分，每个部分包含2个相关数据点（相位噪声、偏移频率）。使用这些数据点，每个部分的面积可以换算为等效的抖动（以秒为单位为表述）。

每个部分对RMS抖动的贡献如图6所示。这些RMS抖动值之和可以使用下列方程式来计算：

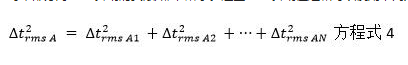
根据这个等式，可以计算出图6中显示的4个区域对抖动的总体贡献之和为434 fs。此值乘以2即得到总噪声贡献△trmsPN）——868 fs。此外，图6中还有2个毛刺。由于这些毛刺在单个频率上，可以使用下列方程式来单独计算及增加它们对抖动的贡献：

每个毛刺的dB值都可以使用方程式3换算为抖动。

图6中显示的示例在1.4 MHz和25 MHz频率时有毛刺，分别为-111 dB和-72.6 dB。1.4 MHz毛刺的等效RMS抖动为6.3 fs，25 MHz毛刺等效RMS抖动为527 fs。较高频率的毛刺对周期抖动的影响比较低频率的毛刺更大。25 MHz毛刺的值要比1.4 MHz毛刺高得多。使用方程式5计算的总毛刺RMS抖动值△trms Spur）极接近于527 fs，因此，1.4 MHz毛刺的影响可以忽略不计。高dB毛刺可能是某些应用中因抖动影响增加而易于出现的误差。使用方程式2，可以估算出图6中描绘图表的总周期抖动为1.015ps。

总而言之，工程师在指定时钟器件时，诸如相位噪声及相位抖动等频域参数对他们极有价值。器件制造商提供的相位噪声图是这些产品的极重要性能指示工具。可以使用图表来近似估算PLL的带宽及抖动传递特性，因而帮助确定它在相关频率范围的特性（作为抖动衰减器或产生器）。也可以根据给定图表来估算周期抖动，方式是考虑主导频率范围内的相位噪声及关键频率时的毛刺。寻求为下一代设计应用指定时钟器件的工程师使用这些信息，可以作出具有更高权威性的产品造型决策。

责任编辑：gt