

浅析量子网络与纠缠传输
电子说
描述
量子网络中,传递信息的基本单位——量子比特 (qubit)——可以以一定的方式相互纠缠在一起。这种量子纠缠是实现量子计算的必需资源。然而,当两个量子比特被分隔开很长距离时,量子纠缠会格外脆弱。幸运的是,人们可以设计一种方案,通过链路路由和中继器,间接地使两个长距离的量子比特成功纠缠在一起。
这种间接式方案被称作为纠缠传输 (entanglement transmission),是量子网络具有的重要优势之一。但如果网络中每条链路自身的传输能力(“纠缠度”)过低,那长距离的量子传输就无法实现。这种长距离量子传输成功与否对于链路自身能力的依赖性,实际上可以映射为一种统计物理理论,即经典渗流理论 (classical percolation theory)。
理论预测:每条链路自身传输能力只有高于某个阈值,才能实现无穷大量子网络中的长距离量子传输。然而人们发现,在某些特殊拓扑结构(比如蜂窝形)的网络中,即使每条链路自身能力低于阈值,也能实现量子传输。这说明经典渗流理论并不足以解释量子网络真正的统计性质。
在此背景下,波士顿大学Xiangyi Meng (孟祥一), 伦斯勒理工Jianxi Gao (高建喜), 与巴伊兰大学Shlomo Havlin三名研究者通过对任意拓扑结构量子网络的研究,提出了一种通粹渗流理论 (concurrence percolation theory)。
该理论与经典渗流类似,但并非建立在概率测度之上,而是建立于一种叫做通粹纠缠度 (concurrence) 的量子纠缠测度。研究者类比于电阻网络的串并联规律,显式写出了通粹渗流理论的连通规则,并预测了常见拓扑结构的量子网络的新的渗流阈值。研究发现,新的阈值显著低于经典渗流理论的预测。同时,研究者给出了任意串并联结构网络下实现新阈值的局域操作与通信方案,支持了理论预测。
这项工作的创新点在于将大尺度的量子网络纠缠传输问题映射为了一种新的统计理论。这种映射极大简化了刻画大尺度量子纠缠的方式,使纠缠传输问题化简成为了一个经典复杂网络中的链路连通问题。该工作以“Concurrence Percolation in Quantum Networks”为题于近日发表在国际物理学期刊Physical Review Letters.
如图1所示,A与B之间纠缠传输的成功与否实际上取决于每条链路的自身传输能力。如果每条链路可以写作一个二体纠缠纯态:
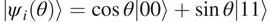
那么存在测度:
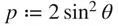
代表了将该二体纠缠纯态转化为最大纠缠纯态(单重态)的概率。同时,该概率可以被理解为链路“开启”的概率。若网络无穷大,可想而知,只有当每条链路“开启”的概率大于某一阈值,才能统计上保证量子网络任意两点间至少有一条完全“开启”的通路,从而实现纠缠传输。
如上思路实际上是一种对经典渗流理论的典型映射。然而,该思路的局限性在于,每条链路不一定需要预先被转化为单重态,亦即不需要成为完全“开启”的状态。
研究发现,即使链路保持在介于“开启”与“关闭”之间(即部分纠缠态),利用可规模化的“确定性 (deterministic) 量子通讯协议”——包括量子纠缠交换协议 (quantum entanglement swapping) 与量子提纯协议 (quantum distillation),无穷大量子网络的任意两点间仍然可以实现纠缠传输。通过分析确定性量子通讯协议的具体表达式,可以得到一种新的映射,建立于concurrence测度(通粹纠缠度)之上:
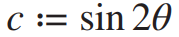
同时,还可以得到基于通粹纠缠度的新的渗流连通规则。
经典渗流理论的连通规则已经被分解为串并联规则(类比于电阻网络),其表达式给出了两点间至少有一条完全“开启”的通路的概率。与之类似,确定性量子通讯协议为通粹渗流理论提供了一套新的串并联规则。此外,基于串并联规则,未知的高阶连通规则可以通过一种star-mesh (SM) 变换进行近似。
基于两种理论不同的串并联规则(及SM变换)得到的渗流阈值(红色竖线,棕色竖线)的对比。通粹渗流理论预测的渗流阈值要显著小于经典渗流理论,意味着即使每条链路的纠缠度小于经典渗流阈值,也可以实现长距离量子传输。实际操作上,由于串并联规则由量子通讯协议直接确定,这表明任何仅由串并联规则构成的串并联结构量子网络都可以通过局域操作与通讯的方式实现通淬渗流理论的结果;
另一方面,尽管SM变换得到的近似高阶连通规则无法由局域操作与通讯实现,但可以通过多链路路由和多体量子协议方案来逼近。
研究者认为,该发现实际上体现了一种“量子优越性”(quantum advantage)。这种“优越性”并非体现于可数个量子比特,而是涌现于统计大尺度上。研究者相信该理论工作不仅可以加深对量子网络功能极限的认识,也可以为量子纠缠统计性质带来新的视角。
本科毕业于北京大学信息科学技术学院、现读于波士顿大学物理系博士生孟祥一为论文的第一作者。伦斯勒理工高建喜教授与巴伊兰大学Shlomo Havlin教授为论文的共同通讯作者。
编辑:jq
-
中国科大成功构建高纠缠效率城域三节点量子网络2024-05-16 1236
-
量子通信和量子纠缠你如何理解2022-12-19 1773
-
量子纠缠是实现量子通信的重要基础2021-01-21 5344
-
量子通信/网络重要进展:我国首次实现远距离量子纠缠纯化,效率提升6000多倍2021-01-13 2346
-
如何建立远距离量子网络关键技术?2020-12-21 2383
-
量子通信网络技术首次实现相距50公里光纤的存储器间的量子纠缠2020-03-17 2931
-
奥地利科学家首次用光缆将量子纠缠传输了50公里2019-09-03 3133
-
南京大学打造出世界首套无人机量子通信网络,使用无人机作为量子传输的中继站2019-07-07 4705
-
中国科大量子纠缠网络首次实现自检验2019-03-13 1211
-
量子网络新突破:量子纠缠理论解决研发障碍2018-11-08 1513
-
美国的两家国家实验室计划建立一个新的量子网络2018-10-31 3602
-
基于量子纠缠和量子隐形传态的网络将带来网络安全、计算以及科学上的飞跃2018-06-20 6786
-
首次实现了25个量子接口之间的量子纠缠2018-06-06 6777
-
全光子量子中继器:迈向全球量子网络2015-04-23 2368
全部0条评论

快来发表一下你的评论吧 !

