复频率与时间函数两者之间的关系解析

复频率现在已是一个广泛熟悉而通用的名词，所以这里仍旧用它。复频率可以方便地表示在一个复平面上，如下图所示。

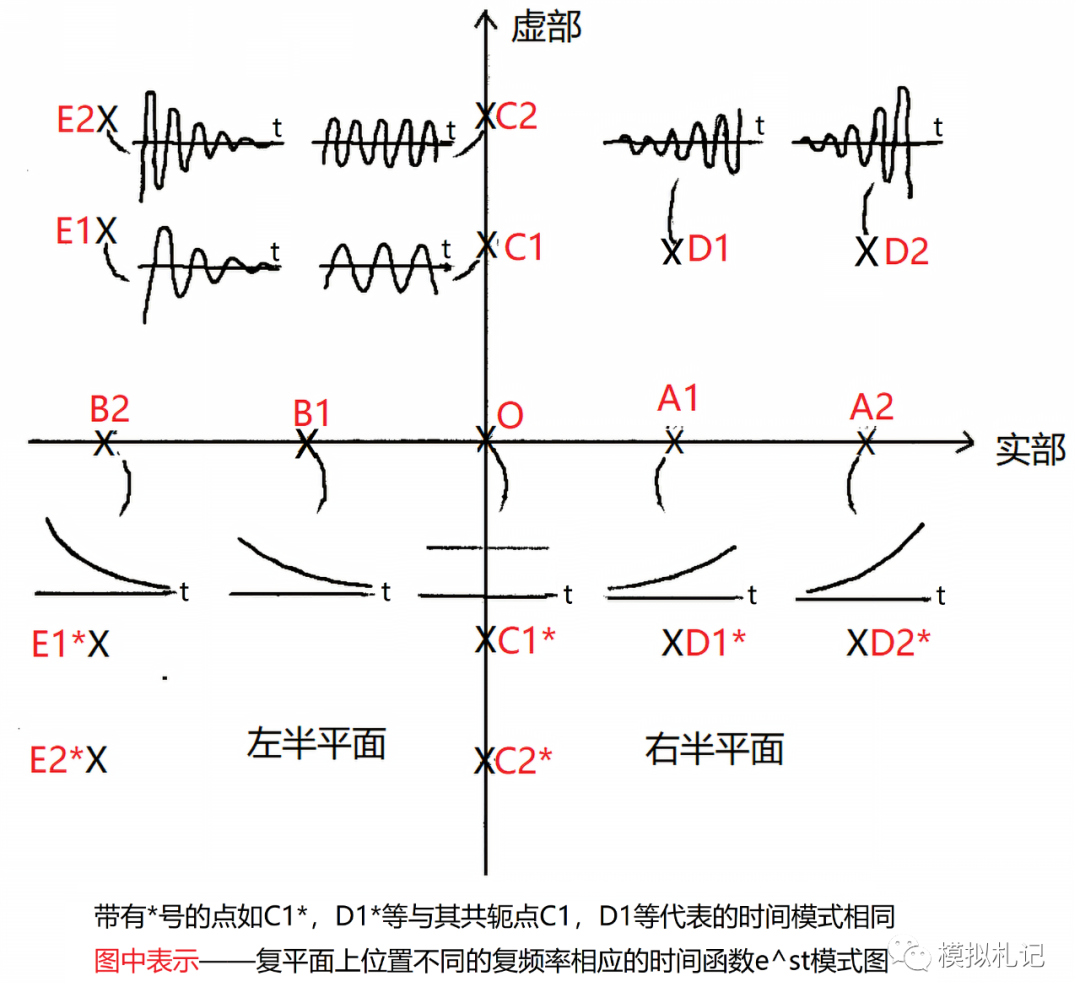
水平轴为实轴(σ轴)，垂直轴为虚轴(jω),则不同的s值应于复平面上不同位置的点。

因为s的虚部ω反应指数函数的频率，而实部σ则反映指数函数的幅度变化率。因此在复平面实轴上的点如A1、A2、B1、B2等。由于ω=0，所代表的是随时间按指数规律单调增长或衰减的指数信号。

在σ正方向上σ>0，代表的是随时间增长的指数信号。在σ轴负方向上σ<0，代表的是随时间衰减的指数信号。且如点的位置距离虚轴愈远，则σ的绝对值愈大，即意味着信号的增长或衰减速率愈大。

(1)试比较点A1与A2及B1与B2。A1、A2在正实轴上，代表的是随时间增长的指数信号，而B1、B2在负实轴上，代表的是随时间衰减的信号。

A1、B1比A2、B2距虚轴较近，所以A1、B1代表的指数信号随时间的变化较A2、B2所代表的信号随时间的变化较慢。

(2)在坐标原点O所代表的信号则是不随时间变化的直流信号。

(3)在虚轴上的点则因为б=0，所以代表的是等幅的正弦振荡信号，且频率随点距实轴的距离增加而增加。

(4)对于既不是实轴又不是虚轴上点，因为s为复数，所代表的是幅度按指数规律变化的“正弦振荡”信号。在做半平面是幅度按指数规律衰减的正弦信号，在右半平面是幅度按指数规律增长的正弦信号。

当然，如果点距离虚轴愈远，则幅度的变化速率愈快，如距实轴愈远，则信号的频率愈高。

通过上面的分析可以看出复平面上的每一点都对应于指数函数的一个确定的模式。需要指出的是在这里也会出现负频率的信号，如C1* 、D1*等。

其原因和傅里叶变换一样，是由于用指数分量来表示信号的结果。

正如傅里叶变换中所指数的一个正频率(s=jω)的指数函数与一个负频率(s=-jω)的指数函数可以合并成一个等幅正弦信号：

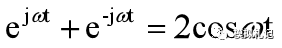
同样两个复频率为共轭对(s=σ+jω,及s=σ-jω)的指数函数也可以合并成一个幅度按指数规律变化的正弦信号：

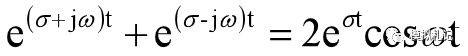
因此任一函数被分解为指数函数之和的时候，其复频率一定是共轭成对出现的，不存在只有一个单独的负频率的情况。

通过上面对复频率的说明，可以更清楚的看到，双边或单边拉普拉斯变换都是把函数分解为无穷多个具有复频率s的指数函数之和。

而傅里叶变换只是双边拉普拉斯变换中s=jω的一种特殊情况，即分解沿着复平面的虚轴进行的。

文章出处：【微信公众号：模拟札记】

责任编辑：gt